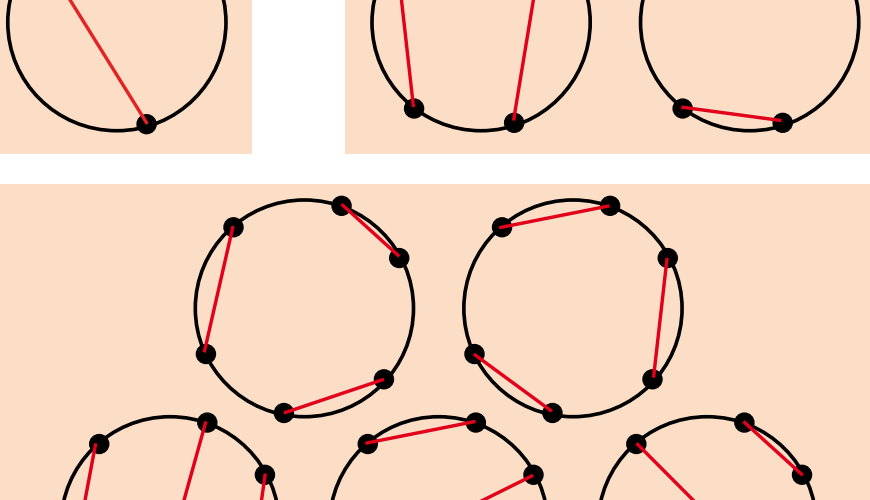
Reeksen à la 1/89
[ooo]
In Pythagoras 63-1 stond het interessante getal $1/89$, waarin op schijnbaar magische wijze zowel de rij van Fibonacci als de machten van $11$ gecodeerd zitten. Beide coderingen werden geïllustreerd door twaalf steeds kleinere decimale getallen bij elkaar op te tellen, in het eerste geval steeds eindigend op het volgende Fibonaccigetal, in het tweede geval steeds eindigend op de volgende macht van $11$. De nieuwsgierige lezer kon hier minstens twee vragen bij stellen: (i) hoe kun je bewijzen dat $1/89$ de som van beide rijtjes is, en (ii) hoe bijzonder is het eigenlijk dat $1/89$ beide getallenrijen bevat? In dit artikel gaan we daar wat verder op in.
Eerst en vooral dit: het is iets typisch voor wiskundigen om oneindig veel getallen bij elkaar op te willen tellen. Het resultaat is ook wel eens (typisch wiskundig) een getal met oneindig veel cijfers na de komma. En dat leidt soms tot onverwachte resultaten. Wist je bijvoorbeeld dat
$$0{,}999999999\dots = 1 ?$$
We kunnen dit eenvoudig als volgt bewijzen, en het bewijs hiervan vormt de basis van het vervolg van dit artikel. Noem wat links staat x, dus x is het getal met 0 voor de komma, en oneindig veel negens na de komma:
$$x = 0{,}999999999\dots$$
Als we $x$ vermenigvuldigen met $10$, dan vinden we:
$$10x = 9{,}999999999\dots$$
met jawel: oneindig veel negens na de komma. Maar als we vervolgens $10x$ min $x$ doen, dan trekken we dus die twee decimale getallen van elkaar af met als resultaat: $9x = 9$ (alle negens na de komma vallen tegen elkaar weg). Oftewel $x = 1$, dus we hebben bewezen dat
$$0{,}999999999\dots = 1.$$
Deze truc kan ook gebruikt worden als niet alle cijfers na de komma gelijk zijn. Voor $x = 0{,}13333\dots$ gaat het als volgt:
|
en dus is $x = 1{,}2/9 = 12/90 = 2/15$. Vermenigvuldigen van je oorspronkelijke getal met een geschikte macht van $10$ levert hier een verschoven decimale uitdrukking op, zodanig dat na aftrekken een eindige decimale ontwikkeling ontstaat. Wellicht heb je geleerd dat zulke decimale getallen met een repeterend gedeelte kunnen worden opgevat als zogenaamde meetkundige reeksen. Door de formule voor de som van een oneindige rij te gebruiken kun je de betreffende repeterende decimale breuk eenvoudig herschrijven als een gewone breuk. Zo is bijvoorbeeld
| $0{,}9999\dots$ | $=$ | $0{,}9+0{,}09+0{,}009+\cdots$ | |
| $=$ | $9\cdot\frac{1}{10}+9\cdot\frac{1}{10^2}+9\cdot\frac{1}{10^3}+\cdots$ | ||
| $=$ | $\displaystyle\sum\limits_{i=1}^{\infty}\frac{9}{10^i}$ |
Elk volgend element in de som ontstaat door zijn voorganger met dezelfde factor, de reden $r$, te vermenigvuldigen. In dit geval is de eerste term $9/10$ en de reden $r = 1/10$. En omdat $|r| = 1/10 < 1$, heeft deze reeks een eindige som en geldt de limietformule
$$\sum_{i=1}^\infty\frac{9}{10^i}=\frac{\rm eerste\ term}{1-{\rm reden}}=\frac{\frac{9}{10}}{1-\frac{1}{10}}=1,$$
precies wat we verwachten. Voor het getal $0{,}137137137137\dots$ vinden we op dezelfde manier:
$$\sum_{i=1}^{\infty}\frac{137}{1000^i}=\frac{\frac{137}{1000}}{1-\frac{1}{1000}}=\frac{137}{999}.$$
De reeks getallen met de machten van $11$ erin was geschreven als de som van
| $0{,}01$ | |
| $0{,}0011$ | |
| $0{,}000121$ | |
| $0{,}00001331$ | |
| $\vdots$ |
ofwel
$\frac{1}{100}\cdot 11^0+\frac{1}{10\,000}\cdot 11^1+\frac{1}{1\,000\,000}\cdot 11^2+\frac{1}{100\,000\,000}\cdot 11^3+\cdots.$
Samengevat is dit de oneindige reeks
$$\frac{1}{100}\sum_{i=0}^{\infty}\left(\frac{11}{100}\right)^i,$$
een meetkundige reeks met reden $11/100$ die convergeert naar
$$\frac{\frac{1}{100}}{1-\frac{11}{100}}=\frac{1}{89}.$$
Wat dan de tweede som in Pythagoras 63-1 betreft: de bovenstaande vermenigvuldig- en verschuiftruc kan ook inzichtelijk maken waarom het getal $1/89$ niet alleen de machten van $11$ bevat, maar ook de rij van Fibonacci.
De Fibonaccirij is gedefinieerd door $F_n = F_{n-1} + F_{n-2}$ met $F_0 = 0$, $F_1 = 1$. De eerste twaalf elementen van de rij zijn: $0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89$.
In Pythagoras 63-1 werd beweerd dat je met deze getallen een rij decimale breuken kunt vormen die precies optelt tot $1/89$. De rij zag eruit als:
| $0{,}01$ | |
| $0{,}001$ | |
| $0{,}0002$ | |
| $0{,}00003$ | |
| $0{,}000005$ | |
| $0{,}0000008$ | |
| $0{,}00000013$ | |
| $\vdots$ |
en leidde opgeteld tot de reeks
$0{,}01\cdot F_1+0{,}001\cdot F_2+0{,}0001\cdot F_3+\cdots = F_110^{-2}+F_210^{-3}+F_310^{-4}+\cdots$
Als je goed oplet, zie je dat dit patroon doorloopt als de Fibonaccigetallen uit meer dan een cijfer gaan bestaan:
$0{,}0000008 = F_610^{-7}$ en $0{,}00000013 = F_710^{-8}$.
Hiermee zien we dat de bewering is dat
$$\frac{1}{89}=\sum_{i=0}^{\infty}F_i10^{-i-1},$$
waarin ook $F_0 = 0$ is meegenomen. Doordat de eerste getallen in de rij allemaal maar uit één cijfer bestaan, kun je het begin van de som $x$ van het rijtje ook gemakkelijk opschrijven als:
$x=0{,}011235\ldots=0{,}F_0F_1F_2F_3F_4F_5\ldots$
waarop we dan de vermenigvuldig- en verschuiftruc kunnen toepassen:
$10x = 0{,}11235\ldots = F_0{,}F_1F_2F_3F_4F_5\ldots$
Wat hebben we hier nu aan? Wel, als je naar de definiërende recurrente betrekking voor de Fibonaccirij kijkt, zie je dat het optellen van de twee getallen hierboven leidt tot iets speciaals: het eerste cijfer na de decimale komma wordt $F_0 + F_1 = F_2$, het tweede cijfer wordt $F_1 + F_2 = F_3$, enzovoort. We krijgen dus na optelling
|
Hierbij is gebruikt dat $F_0 = 0$. Vergelijken met het oorspronkelijke getal $x$ leert dat we nu een verschoven kopie van $x$ hebben, alleen het cijfer $1$ van $F_1 = 1$ ontbreekt voor de komma. Dit betekent dat bovenstaande gelijk is aan
$11x = 0{,}F_2F_3F_4F_5\ldots = 100x - 1$
en daarmee hebben we een vergelijking voor $x$ met als oplossing:
$x=\frac{1}{89}.$
Met de oneindige reeksen
| $x$ | $=$ | $0{,}011235\ldots$ | $=$ | $\sum_{i=0}^{\infty}10^{ -i-1}$ | en | |
| $10x$ | $=$ | $0{,}11235\ldots$ | $=$ | $\sum_{i=0}^{\infty}10^{-i}$ |
kun je dit ook netjes doen door steeds de coëfficiënten van gelijke machten van $10$ op te tellen.
Als je eenmaal snapt hoe deze reeksen in elkaar zitten, begrijp je ook dat $1/89$ zeker niet het enige getal met dit soort leuke coderingen is. Laten we bijvoorbeeld een nieuw getal $y$ vormen door steeds een $0$ voor het volgende Fibonaccigetal toe te voegen:
| $y$ | $=$ | $0{,}01010203050813213455\ldots$ | |
| $=$ | $\sum_{i=0}^{\infty}F_i10^{-2i}$ | ||
| $=$ | $F_0{,}F_10F_20F_30F_4\ldots$ |
Alle cijfers moeten nu twee plaatsen naar voren worden geschoven om weer de truc met de recurrente betrekking te kunnen toepassen, dus we nemen
| $100y$ | $=$ | $1{,}01020305\ldots$ | |
| $=$ | $\sum_{i=0}^{\infty}F_i10^{2-2i}$ | ||
| $=$ | $F_1{,}0F_20F_30F_40F_5\ldots$ |
en tellen de twee uitdrukkingen bij elkaar op, leidend tot
$101y=F_2{,}0F_30F_40F_50F_60\ldots=10000y-100.$
Door deze vergelijking voor y op te lossen weten we dat het gevormde getal gelijk is aan de breuk
$$y=\frac{100}{9899}.$$
Anderzijds kun je deze breuk ook als een som van machten schrijven, door het omgekeerde proces dat we zagen voor $1/89$ te gebruiken:
$$\frac{100}{9899}=\frac{\frac{1}{100}}{1-\frac{101}{10000}}=\frac{1}{100}\sum_{i=0}^{\infty}\left(\frac{101}{10000}\right)^i.$$
Ofwel, in het getal $100/9899$ zitten de Fibonaccirij en de machten van $101$ verborgen. Je kunt beide encoderingen gemakkelijker zien dan in het vorige voorbeeld. De eerste elf Fibonaccigetallen zijn letterlijk terug te vinden in de eerste $21$ cijfers van de decimale ontwikkeling. En de machten van $101$ herbergen heel duidelijk de binomiaalcoëfficiënten zolang ze uit maximaal twee cijfers bestaan:
| $0{,}01$ | ||
| $0{,}000101$ | ||
| $0{,}0000010201$ | ||
| $0{,}00000001030301$ | ||
| $0{,}000000000104060401$ | ||
| $0{,}0000000000010510100501$ | ||
| $0{,}00000000000001061520150601$ | ||
| $0{,}000000000000000107213535210701$ | ||
| $\vdots$ | $+$ | |
| $0{,}01010203050813213455\ldots$ |
Op eenzelfde manier kun je met $p = F_0{,}00F_100F_200F_300F_4\ldots$ komen tot $1001p = 10^6p-1000$ en dus bevat ook $p = 1000/998999$ alle Fibonaccigetallen, waarvan je er nog meer kunt herkennen omdat ze niet 'mengen'. En $p$ bevat alle machten van $1001$. Enzovoort.
We hebben in bovenstaande drie verschillende gevallen bestudeerd waarvoor dit idee werkt met de Fibonaccirij. Wiskundigen hebben dan de neiging om de gebruikte techniek te veralgemeniseren. Dat kan hier als volgt gebeuren: elk van de getallen $F_0{,}F_1F_2F_3F_4\ldots$; $F_0{,}0F_10F_20F_30F_4\ldots$; $F0{,}00F_100F_200F_300F_4\ldots$ is van de volgende vorm:
$$F_0+F_1z+F_2z^2+F_3z^3+F_4z^4+\cdots$$
met $z$ respectievelijk gelijk aan $1/10$, $1/100$ en $1/1000$. Om de bovenstaande truc hier te gebruiken vermenigvuldigen we deze som eerst met $z$ (i.p.v. met $10$ of $100$ of $1000$) en dan met $z^2$:
| $x$ | $=$ | $F_0+$ | $F_1z+$ | $F_2z^2+F_3z^3+F_4z^4+\cdots$ | |
| $zx$ | $=$ | $F_0z+$ | $F_1z^2+F_2z^3+F_3z^4+F_4z^5+\cdots$ | ||
| $z^2x$ | $=$ | $F_0z^3+F_1z^3+F_2z^4+F_3z^5+F_4z^6+\cdots$ |
Als we nu van de eerste vergelijking de tweede en de derde aftrekken, en we maken hierbij gebruik van de recursie van de Fibonaccirij, die zegt dat $F_2 - F_1 - F_0 = 0$, $F_3 - F_2 - F_1 = 0$, …, dan vinden we:
$x(1-z-z^3)=F_0+(F_1-F_0)z$ ofwel $x(z-z-z^2)=z$.
We hebben daarmee de som van de volgende oneindige reeks gevonden, als die som een eindig resultaat geeft natuurlijk:
$F_0+F_1z+F_2z^2+F_3z^3+F_4z^4+\cdots=\frac{z}{1-z-z^2}$.
Deze ene formule bevat alle gevallen met de Fibonaccirij die we hierboven bekeken hebben! In de wiskunde noemen we de uitdrukking in het rechterlid de genererende functie van de rij van Fibonacci. Genererende functies kennen veel toepassingen in de wiskunde. Zie Pythagoras 55-4 (p.25) en 55-5 (p.11) voor meer uitleg.
Je vraagt je nu misschien wel af of het ook zinvol is getallen te bekijken met oneindig veel cijfers vóór de komma. Hiermee bedoelen we niet getallen zoals $\ldots00017652$, die beginnen met oneindig veel nullen, want dat zijn in feite onze 'gewone' getallen zoals $17652$. Neem bijvoorbeeld het gehele getal dat bestaat uit oneindig veel negens: $\ldots9999999$. Kunnen we hier iets mee? Laten we even de truc toepassen van daarstraks: stel
$x = \ldots9999999$.
Als we dan hiermee $10x$ berekenen, dan geeft dit:
$10x = \ldots99999990$.
Om zoveel mogelijk negens weg te werken, berekenen we $x - 10x$ en dat geeft $9$. Dus $-9x = 9$, en dat zou betekenen dat
$\ldots9999999 = -1$.
Dat lijkt dus niet zo interessant, of zelfs irrelevant, alhoewel... Computers gebruiken bijna altijd een voorstelling van getallen waarbij iets gelijkaardigs gebeurt: als een computer bij het 8-bitsgetal $11111111$ (dus allemaal eentjes - binair!) $1$ optelt, dan komt hij uit op het 8-bitsgetal $00000000$, dus voor de computer is $11111111$ blijkbaar gelijk aan $-1$. De schrijfwijze $11111111$ is inderdaad hoe de computer het getal $-1$ voorstelt in de zogenaamde 2-complement notatie, de voorstelling voor gehele getallen die bijna elke computer gebruikt.