Ruimtemeetkunde op de WisFaq
[oOO]
Op de WisFaq kun je vragen over wiskunde stellen. De meeste vragen hebben betrekking op huiswerk maar, zo af en toe wordt er een vraag gesteld waar je een leuk artikel voor Pythagoras van kunt maken. De bedenker van de WisFaq zal regelmatig een vraag bespreken. Hij begint met een vraag over ruimtemeetkunde.
Hier is een vraag uit 2003"In deze toets moet je doorsneden uit een kubus, piramide of cilinder kunnen construeren. Ik heb dit zelf nog nooit geleerd op school en heb geen idee waar ik zou moeten beginnen." WisFaq — Leerling bovenbouw havo-vwo maandag 10 maart 2003 |
||||
De stof uit deze vraag staat niet meer op het examenprogramma, maar was altijd goed voor een paar mooie puzzels. Bekijk het volgende plaatje maar eens.
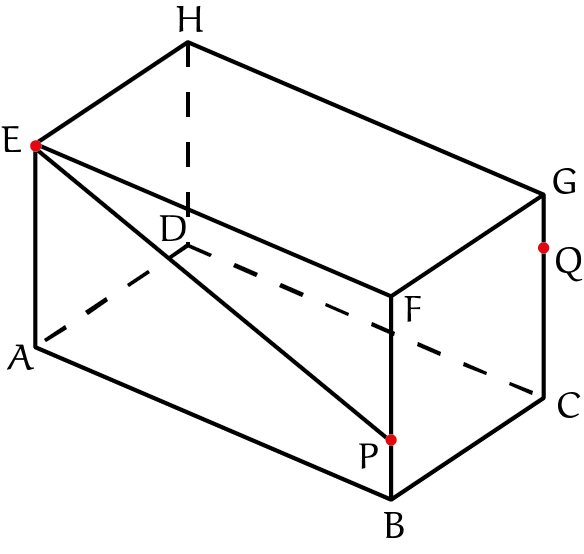
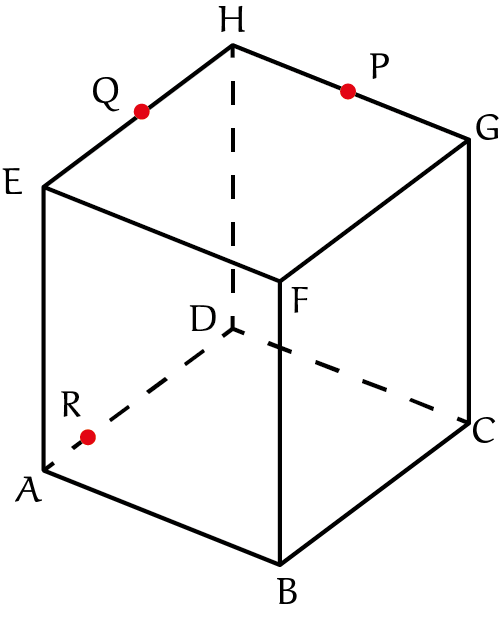
Bij de drie punten $E$, $P$ en $Q$ staat een rode stip. De bedoeling is dat je de snijlijnen van het vlak door die punten met de zijkanten van de balk tekent.
Twee lijnen liggen voor de hand: de verbindingslijnstukken $EP$ en $PQ$ liggen op zijvlakken, dus die geven ons al twee snijlijnen. Voor de andere snijlijnen hebben we een stelling nodig.
Stelling: Als twee evenwijdige vlakken $V$ en $W$ gesneden worden door een derde vlak $U$, dan zijn de snijlijnen evenwijdig.
Dat kun je inzien door zelf twee evenwijdige vlakken te tekenen en die te snijden met een derde; je zult zien dat de snijlijnen inderdaad evenwijdig zijn. We hebben drie paren evenwijdige zijden op de balk, bijvoorbeeld $ABFE$ en $DCGH$. We bekijken deze omdat het lijnstuk $EP$ op het ene, $ABFE$, ligt, en het punt $Q$ op het andere. De snijlijn van ons vlak met $DCGH$ gaat door $Q$ en is evenwijdig aan $EP$. Die tekenen we gestippeld in de tekening omdat hij aan de achterkant ligt.
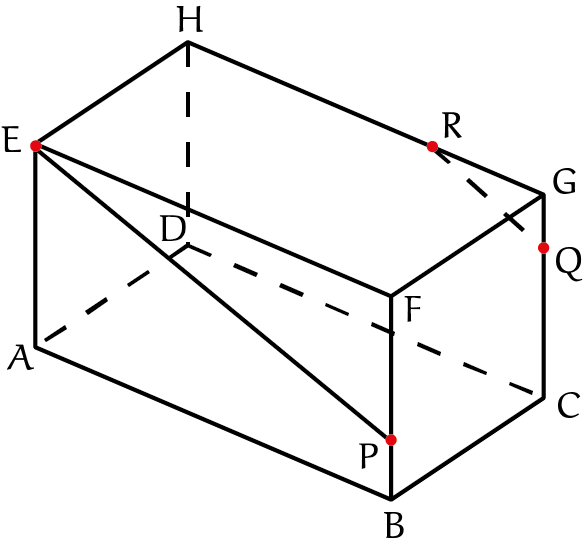
Het snijpunt van die lijn met de ribbe $GH$ noemen we $R$. We zijn nu klaar, want $E$ en $R$ liggen in het zijvlak $EFGH$, dus hun verbindingslijnstuk ook. We kunnen de tekening afmaken.
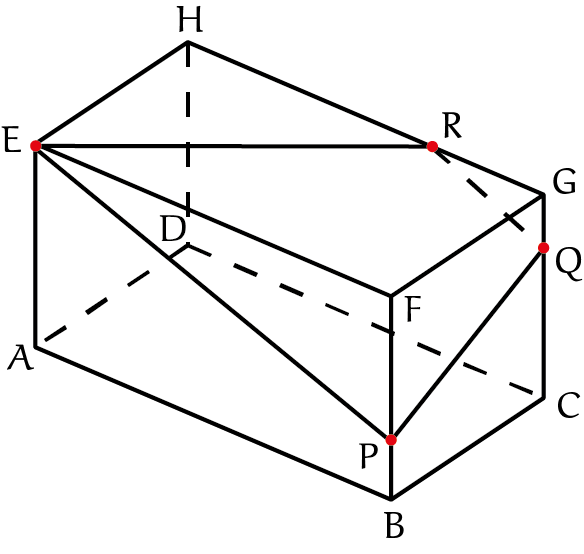
Aan het eind van het artikel staan opgaven om het zelf te proberen. Opgaven 1 en 2 kun je op dezelfde manier oplossen.
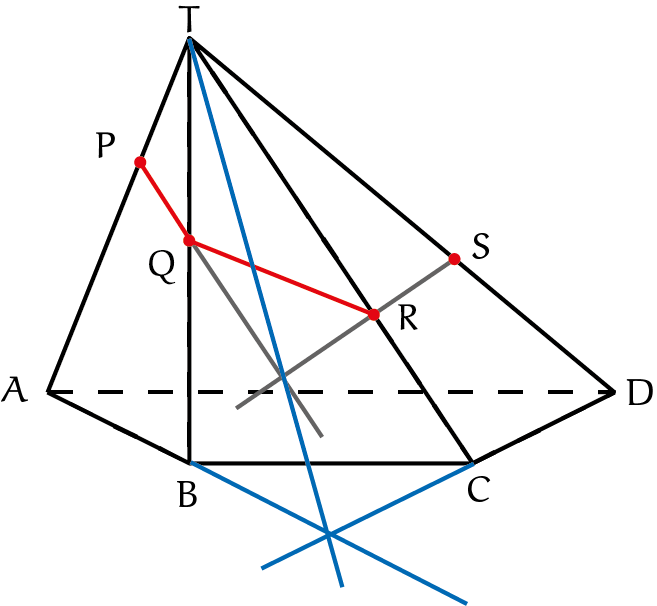
In de vraag werd ook een piramide genoemd. Hier is een voorbeeld van een opgave met drie punten op een piramide. We hebben nu ook zijvlakken die niet evenwijdig zijn, we hebben nog een extra stelling nodig.
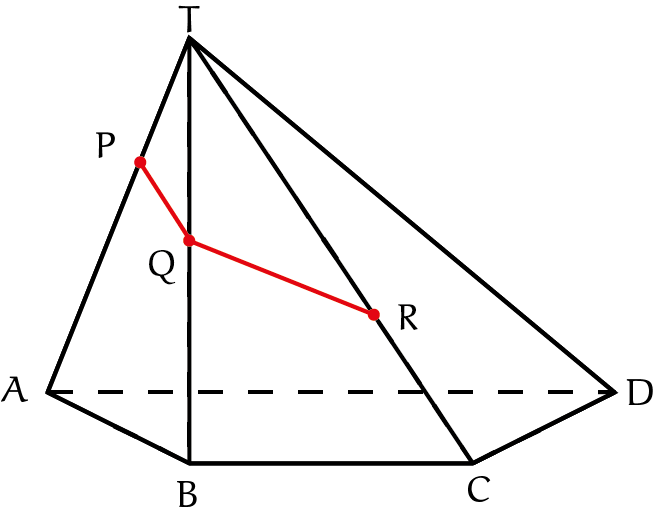
Stelling Als lijn $p$ in het vlak $V$ ligt en de lijn $q$ in het vlak $W$ en ze snijden elkaar in $S$, dan ligt het snijpunt $S$ op de snijlijn van de vlakken $V$ en $W$.
Dit is vrij duidelijk: $S$ ligt op $p$ en $q$ en dus op $V$ en $W$, en daarmee op hun snijlijn. In ons voorbeeld kunnen we de snijlijn van de vlakken door de zijkanten $ABT$ en $CDT$ bepalen en tekenen. Verleng $AB$ en $CD$. Dat geeft twee lijnen op elk vlak één. Hun snijpunt ligt op de snijlijn.
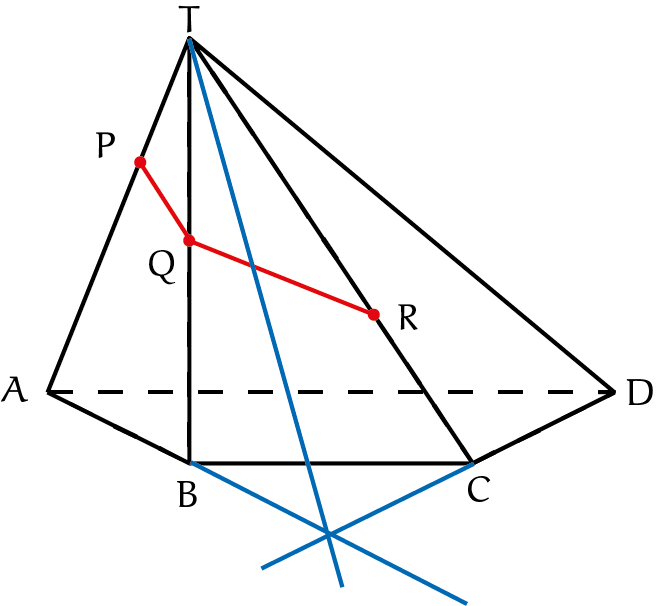
Maar $T$ ligt ook op die snijlijn, dus kunnen we die tekenen (in blauw). De lijn door $P$ en $Q$ snijdt die snijlijn ook. Dat geeft ons het punt op die snijlijn dat in het vlak door onze drie punten gaat. De verbindingslijn van dat punt met $R$ ligt op het vlak door $CDT$ en het snijpunt van die lijn met $DT$ noemen we $S$; we hebben onze derde snijlijn te pakken, nu $P$ en $S$ nog verbinden en we zijn klaar.
Opga
|
Opgave
|
Opg
|
Op
|
Opg
|

 ve 1
ve 1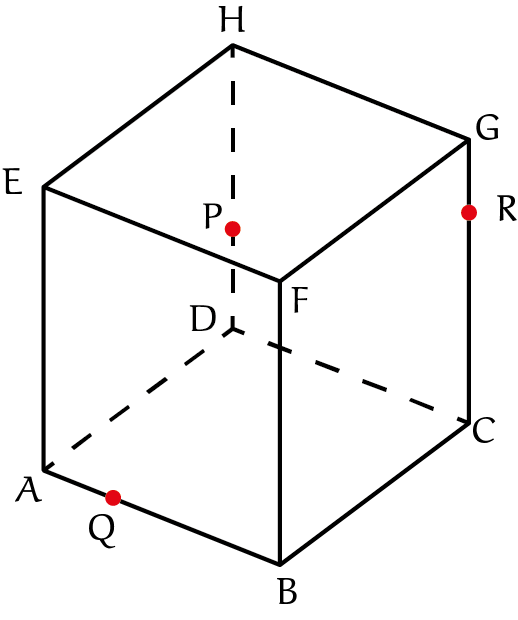 2
2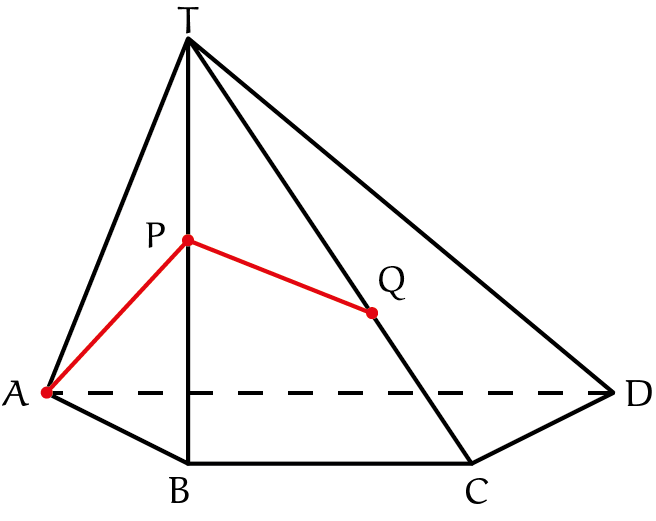 ave 3
ave 3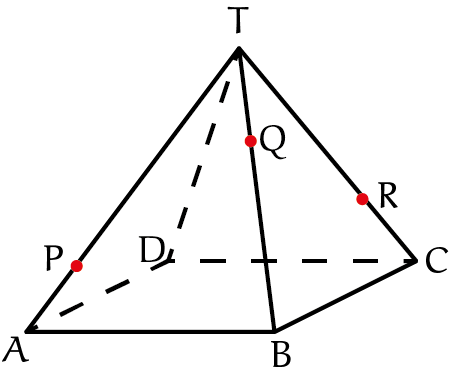 gave 4
gave 4 ave 5
ave 5