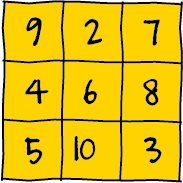De vorige keer begonnen Milli en Mu met een spel met kaarten van 2 tot en met 10 waarbij ze om en om een kaart mochten pakken en degene die als eerste opgeteld 18 kon maken met drie kaarten won. Milli bleef maar winnen, totdat Mu doorhad welk spel het was. Ze speelden boterkaas- en-eieren in vermomming. Op het eerste gezicht lijken deze spellen helemaal niet op elkaar, maar als je de kaarten op de juiste manier in een drie bij drie rooster legt, begint het al ergens op te lijken. Het kan bijvoorbeeld zoals in de figuur hiernaast, maar elke samenstelling waarbij de rijen, kolommen en diagonalen allemaal tot 18 optellen, werkt. Er ligt nu een magisch vierkant. Om het echt boter-kaas-en-eieren te maken, zetten de spelers nu om beurten een O of een X op de kaart die ze kiezen in plaats van de kaart op te pakken.

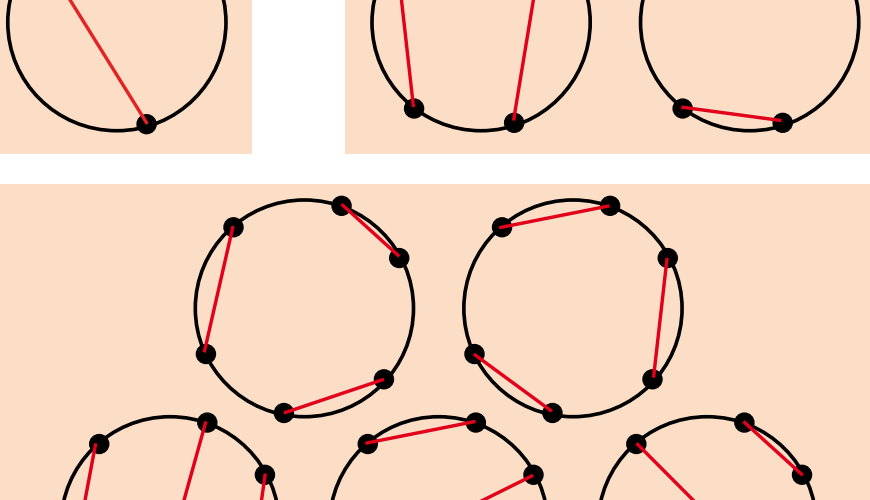
Milli en Mu hebben zich ook aardig vermaakt met het spel Schildpadden redden. Nog evenkort de regels. Je begint met een rij schildpadden, waarvan sommige op hun rug liggen (X) en andere rechtop staan (O). Om de beurt mag je (1) een schildpad die op zijn rug ligt rechtop zetten en (2) eventueel een schildpad verder naar links omkeren (maar dat hoeft dus niet). Wie de laatste schildpad rechtop zet, wint. Hoe speel je dat slim? Schildpadden redden is ook een bekend spel in vermomming, namelijk Nim. Nim speel je met zijn tweeën. Het spel begint met wat stapeltjes muntjes (maar je kunt het ook met groepjes lucifers of snoepjes spelen). Om de beurt haalt een speler van één stapeltje één of meer muntjes weg (eventueel zelfs het hele stapeltje). Wie niet meer kan pakken, verliest. (Soms speelt men het met de regel dat degene die als laatste iets pakt, verliest. Dat doen we hier echter niet.) Probeer het maar eens uit als je begint met drie stapeltjes van $3$, $4$ en $5$ muntjes. Wil je dan beginnen, of liever niet?

We leggen eerst uit hoe je Nim het beste kan spelen. Over Nim is al vaker geschreven in Pythagoras, maar we presenteren hier twee minder gebruikelijke oplossingen. Daarna laten we zien hoe je dat kan gebruiken bij het spelen van Schildpadden redden.

Hoe speel je Nim het beste volgens het algoritme van Pi

Pi wilde aan Milli en Mu uitleggen hoe je bepaalt of je een gegeven Nim spel kunt winnen en als je kunt winnen, hoe je dat dan kunt doen. In 1901 heeft de Amerikaanse wiskundige Charles Bouton beschreven hoe je Nim het beste kan spelen, maar daarbij gebruikte hij de binaire notatie en de XOR operatie op binaire getallen. Pi vond dat te moeilijk en deed het daarom anders. Dit zijn de stappen van het algoritme van Pi, waarbij als voorbeeld drie stapeltjes van $19$, $5$ en $3$ muntjes gebruikt worden. Maak voor elk stapeltje als volgt een onderverdeling in groepjes.

1. Stap $\color{red}{1}$
   1. Leg eerst alle muntjes van het stapeltje apart, d.w.z. in groepjes van grootte
   2. Voeg herhaaldelijk twee groepjes die even groot zijn samen (leg die muntjes op elkaar).
   3. Je bent klaar als alle groepjes verschillen van grootte.
   Ga na hoe het voorbeeld dan uiteen valt in groepjes.
   Bijvoorbeeld: $5 = ///// =/+/+/+/+/ = // + / + / + / = // + // + / = //// + / = 4 + 1$. Net zo vind je $19 = 16 + 2 + 1$ en $3 = 2 + 1$. Het valt je mogelijk op dat de groepjes altijd machten van twee zijn. Maar dat hoef je niet te weten voor dit algoritme.
2. Stap $\color{red}{2}$
   Bepaal of er een groepsgrootte is die een oneven aantal keer voorkomt. Zo nee, dan kun je niet gegarandeerd winnen. Zo ja, dan is er een winnende zet, die we dadelijk bepalen. In het voorbeeld tellen we 3 groepjes van grootte 1, 2 groepjes van 2, 1 groepje van 4 en 1 groepje van 16. De groepsgroottes 16, 4 en 1 komen een oneven aantal keer voor: er kan dus gewonnen worden.
3. Stap $\color{red}{3}$
   Bepaal wat het grootste groepje is dat een oneven aantal keer voorkomt. Je moet dan wat weghalen van een stapeltje waarin zo'n groepje voorkomt. In het voorbeeld is dat grootste groepje dat een oneven aantal keer voorkomt $16$ en wel alleen in het stapeltje met $19$ muntjes.
4. Stap $\color{red}{4}$
   We weten nu van welk stapeltje we gaan pakken. Dat pakken willen we zodanig doen dat de andere speler alleen maar groepsgroottes overhoudt die een even aantal keer voorkomen. Beschouw elke groepsgrootte die een oneven aantal keer voorkomt (in het voorbeeld: 16, 4 en 1). Als die ook voorkomt in het gekozen stapeltje, dan neem je dat groepje weg (om het aantal even te maken). En als het niet voorkomt in het gekozen stapeltje, dan leg je zo'n groepje erbij (om het aantal van die groepjes even te maken). In het voorbeeld halen we dus 16 en 1 weg en leggen er 4 terug. In totaal zijn er van het stapeltje van 19 = 16 + 2 + 1 nu 4 + 2 = 6 muntjes overgebleven. De volgende speler krijgt dan stapeltjes van 6 = 4 + 2, 5 = 4 + 1 en 3 = 2 + 1. Hierin komt elke groepsgrootte een even aantal keren voor.

De reden dat dit algoritme werkt, is de volgende. Als je van zo'n grootste groepje er $1$ afhaalt, valt de rest uiteen in kleinere groepjes waarbij elke kleinere groepsgrootte één keer voorkomt. Bijvoorbeeld $16 - 1 = 15 = 8 + 4 + 2 + 1$. Je kan als het nodig is dus altijd voldoende terugleggen in Stap $\color{red}{4}$.

Laten we ook even het Nim spel met stapeltjes van $3$, $4$ en $5$ muntjes analyseren. Eerst splitsen we de stapeltjes volgens Stap $\color{red}{1}$: $3 = 2 + 1, 4 = 4, 5 = 4 + 1$. Er is een groepsgrootte die een oneven aantal keer voorkomt en wel $2$ in het stapeltje van $3$ (Stap $\color{red}{2}$). Dus degene die aan zet is kan winnen. Het grootste groepje dat een oneven aantal keer voorkomt is diezelfde $2$ (Stap $\color{red}{3}$). Volgens Stap $\color{red}{4}$ halen we $2$ van de $3$ weg en hoeven niets terug te leggen. De tegenstander zit nu met $3 - 2 = 1, 4 = 4$ en $5 = 4 + 1$, waarin alle groepsgroottes een even aantal keren voorkomen. Deze zet hadden we al in de vorige aflevering gezien bij het voorbeeld voor Schildpadden redden. Werk nu zelf het spel uit dat begint met $4$, $5$ en $6$.

ReCursief algoritme van Phi

Phi is echter niet helemaal gelukkig met dit algoritme van Pi. Het is wel heel elementair en voor mensen redelijk uit het hoofd te doen, maar niet zo makkelijk te programmeren (probeer het maar). Phi heeft nog eens nagedacht en kwam met een leuk recursief algoritme (het kader legt uit wat recursie inhoudt). Het algoritme van Phi werkt als volgt:

1. Stap $\color{blue}{1}$
   Als er geen muntjes meer zijn, dan heb je verloren.
2. Stap $\color{blue}{2}$
   Als er nog wel muntjes liggen, beschouw dan het Nim spel dat je krijgt door elk stapeltje te halveren en een eventuele
   rest weg te laten. In het voorbeeld met stapeltjes van $3$, $4$ en $5$ krijg je als 'halve' spel dan: $1$, $2$ en $2$.
3. Stap $\color{blue}{3}$
   Bepaal (recursief, d.w.z. ga hiervoor terug naar Stap $\color{blue}{1}$) of je dit 'halve' spel kan winnen en zo ja, hoe.
   1. Stel je kunt het halve spel niet winnen. Als het totale aantal muntjes even is, dan kun je het 'hele' spel ook niet winnen. Maar als het totaal oneven is, dan kun je het winnen door $1$ weg te nemen van een oneven stapeltje. Daarmee laat je een even totaal achter.
   2. Stel je kunt het 'halve' spel wel winnen, namelijk door $K$ muntjes achter te laten van een stapeltje met $S$ muntjes. Dan kun je het 'hele' spel ook winnen en wel door van het oorspronkelijke stapeltje (van $2S$ of $2S +1$ muntjes) $2K$ of $2K+1$ achter te laten, zodanig dat het achtergebleven totaal van alle stapeltjes even is.

Laten we dit eens toepassen op het spel dat begint met stapeltjes van $19$, $5$ en $3$. In de tabel hieronder zetten we van boven naar beneden (↓) de gehalveerde spellen, terwijl we daarna van beneden naar boven (↑) vaststellen of elk spel te winnen is en zo ja, hoe. Of iets even of oneven is wordt wel pariteit genoemd.

Stapeltje A ↓	Stapeltje B ↓	Stapeltje C ↓	Pariteit totaal ↑	Te winnen ↑	Stapeltje ↑	Achterlaten ↑
$19$	$5$	$3$	Oneven	Ja	A	$2 \times 3 = 6$
$9$	$2$	$1$	Even	Ja	A	$2 \times 1 + 1 = 3$
$4$	$1$	$0$	Oneven	Ja	A	$2 \times 0 + 1 = 1$
$2$	$0$	$0$	Even	Ja	A	$2 \times 0 = 0$
$1$	$0$	$0$	Oneven	Ja	A	$1 - 1 = 0$
$0$	$0$	$0$	Even	Nee	n.v.t.	n.v.t.

 

	Oefen het algoritme van Phi zelf eens met $10$, $8$ en $6$. We geven de tabel met de halve spellen ingevuld (de verdere uitwerking staat op de website).
	Stapeltje A ↓	Stapeltje B ↓	Stapeltje C ↓	Pariteit totaal ↑	Te winnen ↑	Stapeltje ↑	Achterlaten ↑
	10	8	6
	5	4	3
	2	2	1
	1	1	0
	0	0	0	Even	Nee	n.v.t.	n.v.t.
	Ga ook na hoe het zit als je met stapeltjes van $3$, $4$ en $5$ muntjes begint of met $4$, $5$ en $6$.

SChildpadden redden

Zo, nu weet je hoe je perfect Nim speelt. Hoe kun je die kennis gebruiken bij Schildpadden redden?

1. Gegeven een rij schildpadden, maak voor elke schildpad die op zijn rug ligt een stapeltje van $N$ muntjes, waarbij $N$ de positie (van links geteld) is van die schildpad. Er ontstaan dus evenveel stapeltjes als er schildpadden op hun rug liggen.
2. Als je bij Nim het beste van het stapeltje met $M$ muntjes er $K$ (met $K < M$) kan laten liggen (zodat je er dus $M - K$ afhaalt), draai dan de schildpad op positie $M$ rechtop.
3. Als $K = 0$ is, dan laat je het daarbij (en is het stapeltje van $M$ muntjes verdwenen).
4. Als $K > 0$ is, draai dan de schildpad op positie $K$ ook om. Als die schildpad oorspronkelijk rechtop stond, dan ligt die nu op zijn rug, wat overeenkomt met het weghalen van $M - K$ muntjes van het stapeltje van $M$ muntjes, zoals dat ook in het Nim spel gebeurt. 
5. Als die schildpad echter oorspronkelijk op zijn rug lag, dan betekent dit dat er in het Nim spel al een stapeltje van $K$ muntjes lag. Door het rechtop zetten van die schildpad hebben we beide stapeltjes van grootte $K$ dus weggehaald. Uit het algoritme van Pi blijkt dat dit verder niet uitmaakt voor wie er gaat winnen, omdat het de pariteit (het even of oneven zijn) van de groepsgroottes niet verandert.

Omgekeerd, als je weet hoe je Schildpadden redden goed kan spelen, dan kun je dat gebruiken om Nim goed te spelen. Denk daar maar over na. Onder de knop [Bekijk oplossing] vind je binnenkort ook wat Python code om mee te experimenteren. 

		ReCursie Een recursieve definitie definieert iets in termen van zichzelf: 'recurrere' is Latijn voor 'teruglopen'; op zichzelf teruggrijpen. Dat klinkt circulair en daarom wiskundig ontoelaatbaar. Maar het kan wel degelijk goed uitpakken. Hier is een recursieve definitie van het product van een lijst getallen: het product van de lege lijst is $1$ en het product van een lijst met eerste element $a$ en rest in lijst $t$ is $a \times$ product van $t$. Dit werkt omdat de lege lijst als basis van een recursie fungeert en de rest van de lijst korter is dan de oorspronkelijke lijst. Bij het invullen van de tabel voor het algoritme van Phi zie je twee fases: naar beneden worden spellen 'gehalveerd' en de basis is het spel met allemaal lege stapels, vervolgens wordt in de fase naar boven (op de terugweg) de uitslag en beste zet bepaald. Halveren leidt uiteindelijk in een eindig aantal stappen altijd tot het basisgeval.

Bekijk oplossing