Antwoorden Op zoek naar gulden reChthoeken en driehoeken
Opgave 1
$\displaystyle{\frac{1+x}{1}=\frac{1}{x} \Rightarrow x^2+x-1=0 \Rightarrow x=\frac{-1+\sqrt{5}}{2}}$.
$\displaystyle{\varphi = 1+x=\frac{1+\sqrt{5}}{2}}$.
Het tweede vierkant heeft een oppervlakte van $\displaystyle{x^2=\frac{3-\sqrt{5}}{2}}$.
De oneindige meetkundige som van de oppervlakten van de vierkanten is $\displaystyle{\frac{1}{1-\left(\frac{3-\sqrt{5}}{2}\right)^2}=\frac{1+\sqrt{5}}{2}=\varphi}$.
Opgave 2
$\displaystyle{\frac{b+x}{2}=\frac{1}{x}}$ en $\displaystyle{x=\frac{-b+\sqrt{b^2+4}}{2}}$ en $\displaystyle{c=\frac{b+\sqrt{b^2+4}}{2}}$.
De oneindige meetkundige som van de oppervlakten van de rechthoeken is
| $\displaystyle{\frac{b}{1-\left(\frac{-b+\sqrt{b^2+4}}{2} \right)^2}}$ | $$=$$ | $\displaystyle{\frac{b}{1-\frac{2b^2+4-2b\sqrt{b^2+4}}{4}}}$ |
| $$=$$ | $\displaystyle{\frac{4b}{-2b^2+2b\sqrt{b^2+4}}}$ | |
| $$=$$ | $\displaystyle{\frac{2}{-b+\sqrt{b^2+4}}}$ | |
| $$=$$ | $\displaystyle{\frac{2\left(b+\sqrt{b^2+4}\right)}{\left(-b+\sqrt{b^2+4}\right)\left(b+\sqrt{b^2+4}\right)}}$ | |
| $$=$$ | $\displaystyle{\frac{b+\sqrt{b^2+2}}{2}}$ |
Opgave 3
$b=x \Rightarrow 2b=-b+\sqrt{b^2+4} \Rightarrow 3b=\sqrt{b^2+4}\Rightarrow 8b^2=4 \Rightarrow b=\tfrac{1}{2}\sqrt{2}$.
Deze verhouding wordt gebruikt bij A-formaat papier.
Opgave 4
Aangezien $b^2+4>b$ kan $c$ nooit $1$ zijn. Een vierkant is toch op te vullen met een meetkundige reeks van gelijkbenige rechthoekige driehoeken.
Opgave 5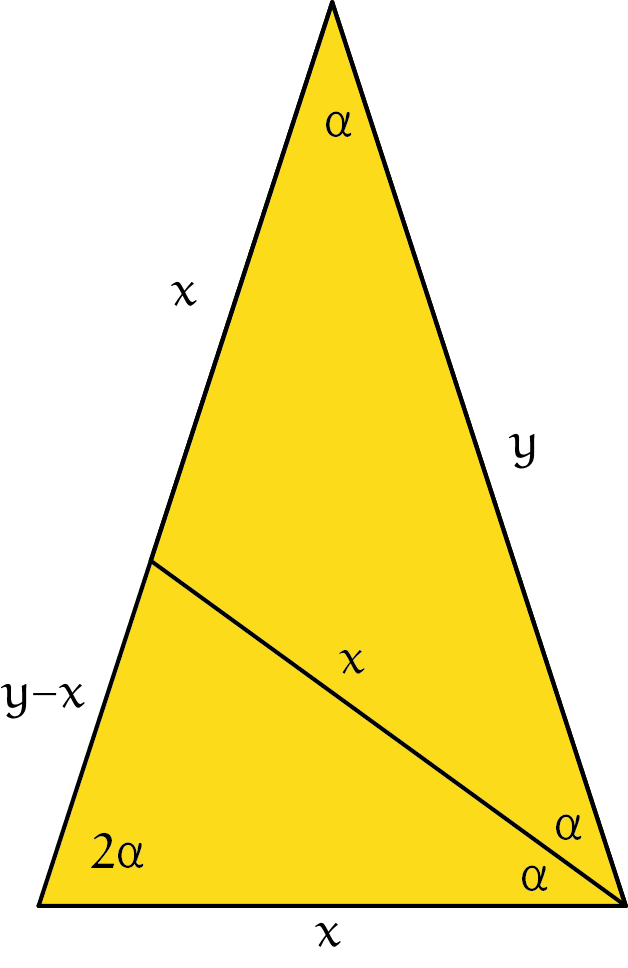
Gebruik de som van de hoeken in een driehoek en verhoudingen van de zijden in gelijkvormige driehoeken. Hiernaast is figuur 5 nog een keer getekend, met lengtes en hoeken benoemd. Hoek $\alpha =36^{\rm o}$ en de verhouding $\displaystyle{\frac{y}{x}=\frac{1+\sqrt{5}}{2}}$. Een soortgelijke berekening geld voor de rechter driehoek in figuur 5.
Opgave 6
Noem in de linkerdriehoek van figuur 6 de lengtes in de grootste driehoek $x$ en $\varphi x$ Dan is de hele oppervlakte gelijk aan $\displaystyle{\frac{x^2\varphi^2\sin(36^{\rm o})}{2}}$. De meetkundige som is gelijk aan $\displaystyle{\frac{\frac{x^2\varphi\sin(36^{\rm o})}{2}}{1-\frac{1}{\varphi^2}}=\frac{x^2\varphi^2\sin(36^{\rm o})}{2}}$, aangezien $\varphi^2-1=\varphi$. Een soortgelijke berekening geldt ook voor de rechterdriehoek in figuur 6.
Opgave 7
De drie hoeken zijn $\alpha$, $\beta - \alpha$ en $\alpha + \gamma$.
Opgave 8
Maak gebruik van de verhoudingen in gelijkvormige driehoeken:
$\displaystyle{x=\frac{a^2}{b}}$, $\displaystyle{y=b-x = \frac{b^2-a^2}{b}}$ en $\displaystyle{z=\frac{ac}{b}}$.
Opgave 9
De oppervlakte van driehoek $ABC$ is $\displaystyle{\frac{b\cdot c\cdot\sin(\alpha)}{2}}$.
De som van de driehoeken met de vorm van driehoek $BCD$ is
$\displaystyle{\frac{\frac{y\cdot c\cdot\sin(\alpha)}{2}}{1-\frac{a^2}{b}}=\frac{b\cdot c\cdot\sin(\alpha)}{2}}$.
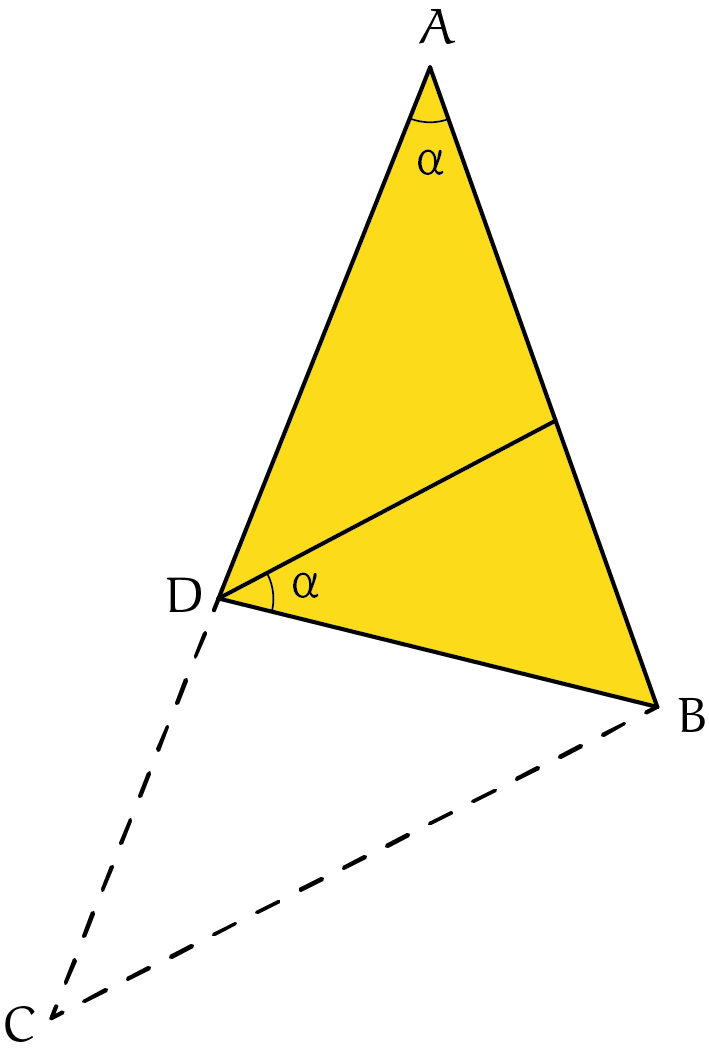Opgave 10
Snij hoek $A$ (met grootte $\alpha$) uit hoek $ADB$ en de driehoek boven heeft hoeken $A$, $B$, en $C$. Dus de driehoeken $ABC$ en $ABD$ zijn partnerdriehoeken van elkaar net zoals de gulden snede driehoeken.
Opgave 11
Dit zijn de gelijkbenige driehoeken.
Opgave 12
Begin met $[\alpha, \beta, \gamma]$ waar $\alpha \le \beta \le \gamma$. Dan zijn de mogelijke partnervormen:
- $\alpha, \beta-\alpha, \beta+\gamma$
- $\alpha, \gamma-\alpha, \alpha+\beta$
- $\beta, \gamma-\beta,\alpha+\beta$
Deze drie zijn echt anders dan $[\alpha,\beta,\gamma]$ tenzij $\gamma-\alpha=\beta$ en dan zijn 2. en 3. hetzelfde als $[\alpha,\beta,\gamma]$. Dit zijn de driehoeken met $\gamma=\alpha+\beta \Rightarrow \gamma=90^{\rm o}$. De hoeken zijn dan gelijk maar de opvullingen zien er anders uit tenzij $\alpha=\beta$ (zie de figuur hieronder)
 |
 |
Opgave 13
Begin weer met $[\alpha,\beta,\gamma]$ waar $\alpha \le \beta \le \gamma$. Dan zijn de mogelijke partnervormen:
- $\alpha, \beta-\alpha, \beta+\gamma$
- $\alpha, \gamma-\alpha,\alpha+\beta$
- $\beta,\gamma-\beta,\alpha+\beta$
Deze drie zijn allemaal echt verschillend tenzij $\gamma = \alpha+\beta \Rightarrow \gamma=90^{\rm o}$ en ook dan zien de opvullingen er anders uit.
Opgave 14
Voor het lukken van dit proces moet de driehoek twee ongelijke hoeken hebben. Gelijkzijdige driehoeken zijn dus uitgesloten. Ze zijn op te vullen met $[30^{\rm o},60^{\rm o},90^{\rm o}] driehoeken maar die vormen geen meetkundige reeks.
Opgave 15
$$\underset{\uparrow \downarrow}{[54^{\rm o},54^{\rm o},72^{\rm o}]} \ \underset{\uparrow \downarrow}{[18^{\rm o},18^{\rm o},144^{\rm o}]}$$
$$\underset{\searrow \nearrow\ \ \searrow \nearrow\ \ }{[18^{\rm o},72^{\rm o},90^{\rm o}]}\underset{\ }{\rightleftharpoons [18^{\rm o},54^{\rm o},108^{\rm o}]\rightleftharpoons[18^{\rm o},36^{\rm o},126^{\rm o}]\rightleftharpoons}\underset{\searrow \nearrow\ \ \searrow \nearrow\ \ }{[36^{\rm o},54^{\rm o},90^{\rm o}]} $$
