Opgave 1

$\tan(\alpha)=\frac{r}{d},$ dus $2\alpha=2\cdot\tan^{-1}\left(\frac{r}{d}\right).$

Opgave 2

a) $2\alpha=90^{\rm o}.$ Dus $\tan^{-1}\left(\frac{3}{d}\right)=45^{\rm o}.$  Dus $d = 3$ cm.

b) $62^{\rm o}, 33^{\rm o}, 23^{\rm o}, 17^{\rm o}, 14^{\rm o}$ en $11^{\rm o}.$

Opgave 3

a) Zie de figuur hieronder.

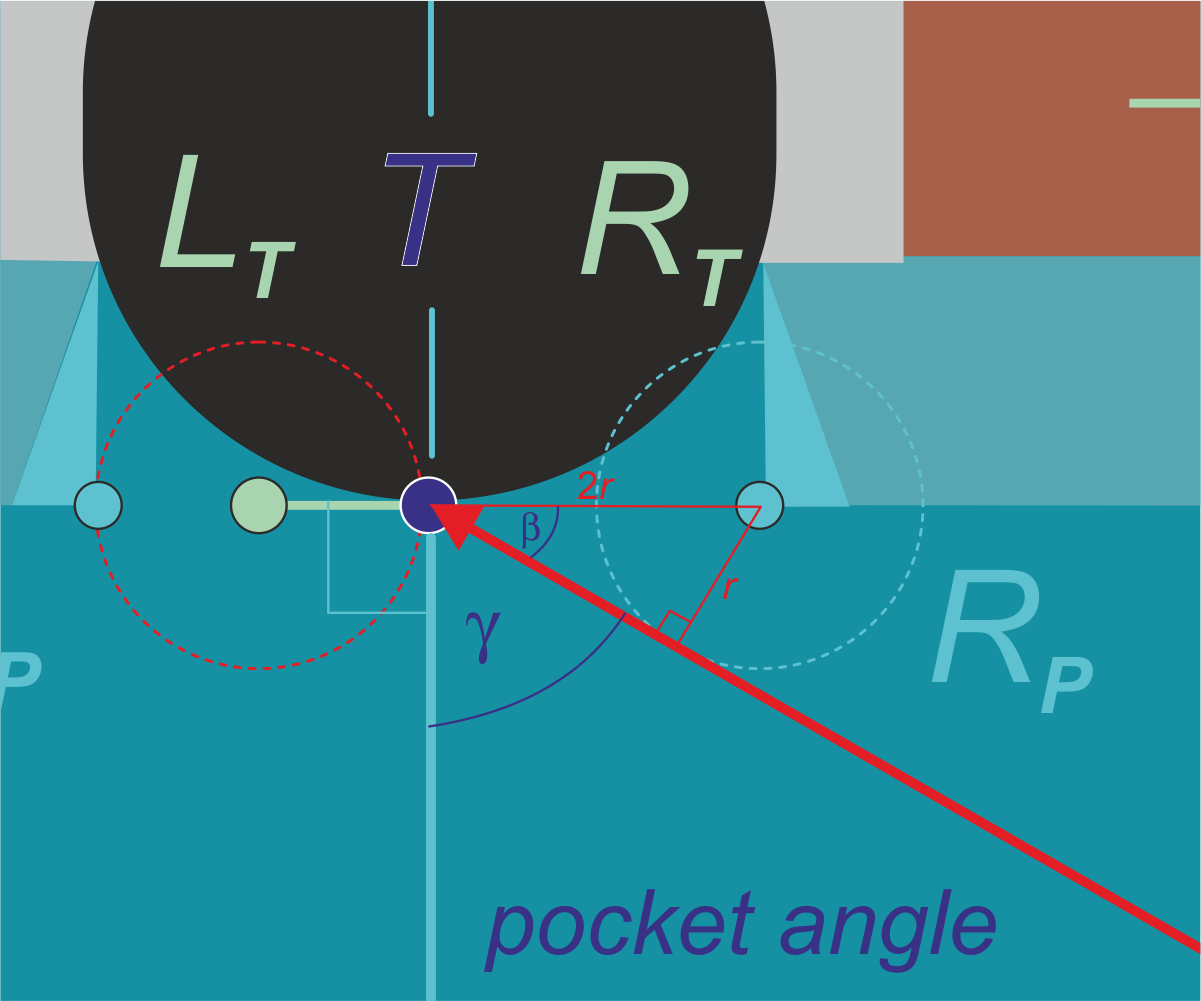
$\sin(\beta)=\frac{1}{2},$ dus $\beta=\sin^{-1} \left(\frac{1}{2}\right)=30^{\rm o}.$ Daaruit volgt $\gamma=90^{\rm o}-\beta=60^{\rm o}.$

b) Lijnstuk $L_TP=\frac{1}{2}L_TR_T.$

c) Willem heeft deels gelijk. De target line moet op de bissectrice van $\angle L_TOP$ gericht worden om de grootste potkans te krijgen. Deze bissectrice verdeelt het potbare gebied in twee ongelijke stukken. Maar bij een kleine foutmarge is het verschil te verwaarlozen.

Opgave 4

Zie de figuur hieronder.

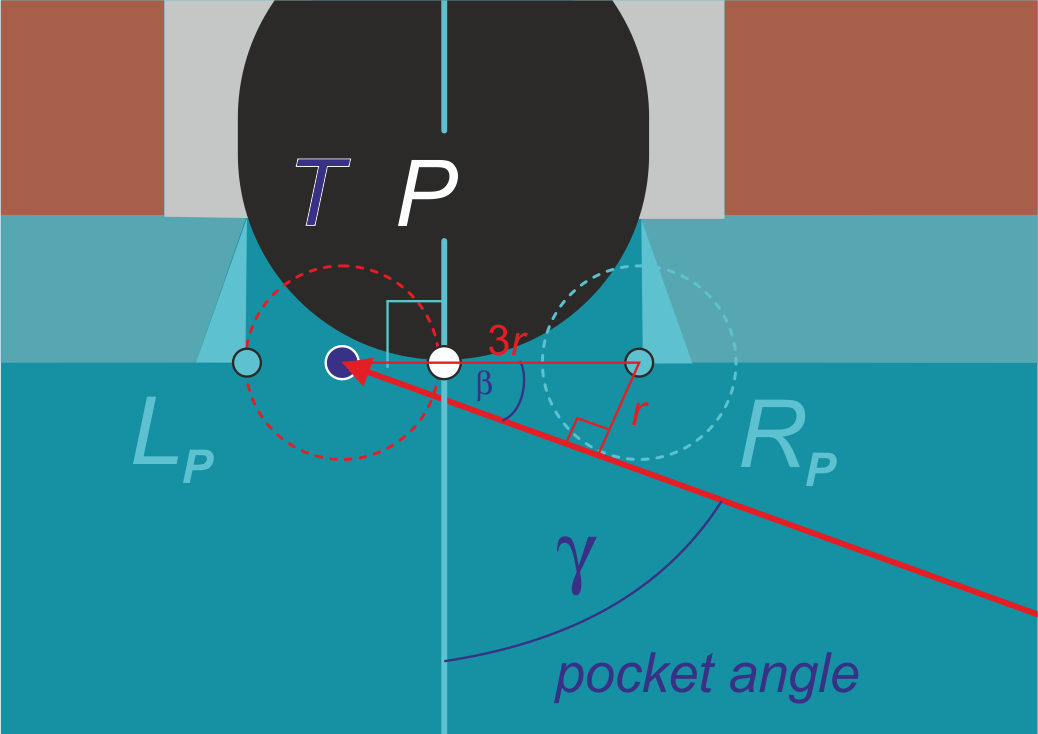
$\sin(\beta)=\frac{1}{3},$ dus $\beta=\sin^{-1}(\frac{1}{3})\approx 19{,}47^{\rm o}.$ Daaruit volgt dat $\gamma=90^{\rm o}-\beta\approx 71^{\rm o}.$

Opgave 5

a) $\sin(\alpha) \approx \tan(\alpha),$ dus $\frac{r}{d}=\frac{x}{2r}.$

b) $\beta(D-d-2r)=x=\frac{2r^2}{d}.$

Opgave 6

$\beta^\prime(d)=\frac{-2r^2(D-2d-2r)}{\left(d(D-d-2r)\right)^2}.$

Stel $\beta^\prime(d) = 0$, waaruit volgt: $d_{\rm min}=\frac{D}{2}-r\approx\frac{D}{2}.$

De hoek is een minimum, omdat $\beta^\prime(d)<0$ voor $d < d_{\rm min}$ (dalende functie) en $\beta^\prime(d)>0$ voor $d > d_{\rm min}$ (stijgende functie). Voor de minimale hoek $\beta_{\rm min}$ geldt dan bij benadering $\beta_{\rm min}\approx 8\left(\frac{r}{D}\right)^2.$

Opgave 7

Bij benadering geldt dat $2\cdot\beta_{\rm min}\approx 2\cdot 8\left(\frac{3}{280}\right)^2\approx 0{,}002 {\rm \ rad} = 0{,}0018\ldots\cdot\frac{180}{\pi}\approx 0{,}1^{\rm o}.$

Dit toont aan dat Willem gelijk heeft en het een erg moeilijke stoot is.