De oude Grieken, en zij niet alleen, deden veel waarnemingen aan de sterren en planeten om te zien en te achterhalen hoe het heelal werkte. 

De posities van de hemellichamen werden met graden, minuten, en seconden genoteerd en bijgehouden, zodat men kon gaan voorspellen wanneer bepaalde gebeurtenissen zoals zons- en maansverduisteringen zouden plaatsvinden.

Moeilijker was het bepalen van afstanden tussen hemellichamen. Het probleem is duidelijk: als je de hoeken tussen allerlei lijnstukken kent kun je met behulp van de sinus- en cosinusregels wel de verhoudingen van de afstanden bepalen maar niet de afstanden zelf. 

Aristarchus van Samos, die in de derde eeuw voor Christus leefde, heeft geprobeerd iets over groottes van, en afstanden tussen, de Aarde, de Maan, en de Zon te zeggen. Hij schreef het op in een boek met de titel Over de afmetingen en afstanden van de Zon en de Maan; je kunt dat online lezen.

In dat boek vinden we

Propositie 7 De afstand van de Zon tot de Aarde is groter dan achttien maal, en minder dan twintig maal, de afstand van de Maan tot de Aarde.

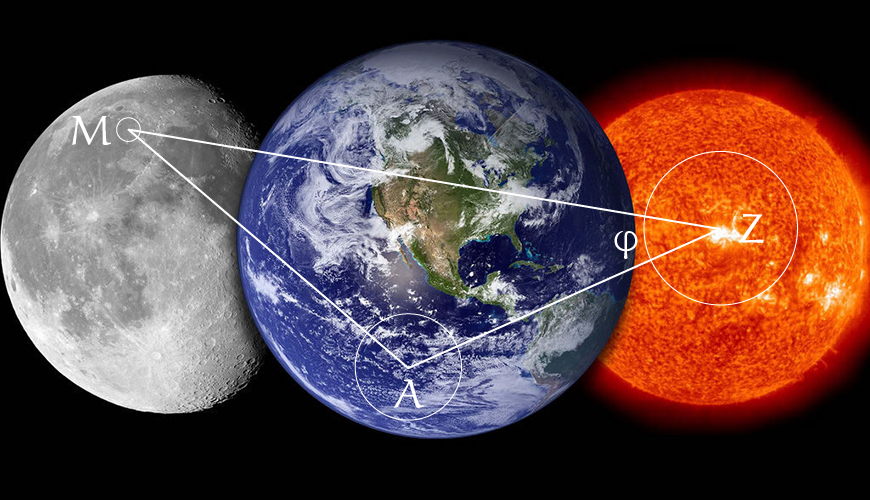
Hoe bewees Aristarchus dat? Dat gaan we nu bekijken. We laten de letters $A$, $M$, en $Z$ voor de Aarde, Maan, en Zon staan.

Een hoek meten

Het eerste dat Aristarchus deed was een rechthoekige driehoek maken met het lijnstuk $AZ$ als hypothenusa (figuur 1). Hij ging ervan uit dat het licht van de Maan eigenlijk van de Zon komt en bedacht toen dat bij halve maan de hoek $\angle ZMA$ recht moet zijn. De Zon kan immers maar de helft van de Maan verlichten en bij halve maan staat onze kijkrichting dan loodrecht op de stralen van de zon.

Aristarchus probeerde de hoek $\varphi$ zo goed mogelijk te meten en kwam uit op, zoals hij het uitdrukte, één-dertigste van een kwart cirkel.

Wij zouden gewoon $3^{\rm o}$ zeggen, en zonder al te veel moeite met behulp van een rekenmachientje de gewenste verhouding bepalen:

$$\frac{AZ}{AM}=\frac{1}{\sin(3^{\rm o})}\approx 19{,}1$$

Maar in de tijd van Aristarchus waren de goniofuncties er nog niet echt en het was nog niet zo eenvoudig een verhouding als $AZ : AM$ te bepalen of af te schatten. Maar het lukte Aristarchus, met behulp van wat stellingen uit de meetkunde, toch. De twee afschattingen gaan op nogal verschillende manieren.

Groter dan 18

Bij deze afschatting gebruiken we figuur 2.

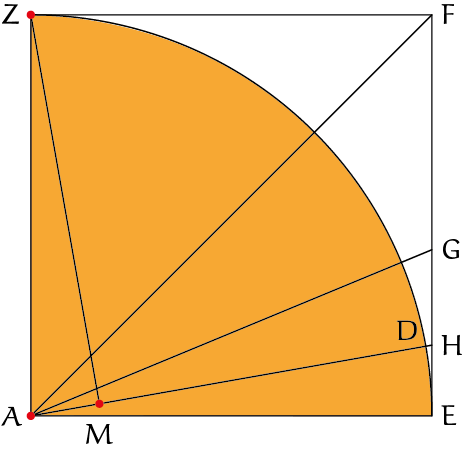
Deze is als volgt opgebouwd. We zijn begonnen met de driehoek $AMZ$, op het moment van de halve maan. Dan is $\angle ZM$ is dus één-dertigste van een rechte hoek. We zetten een vierkant $AEFZ$ op de lijn $AZ$, en we trekken de kwart cirkelboog om $A$ van $E$ naar $Z$.

De boog $ZE$ is een deel van de baan van de Zon om de Aarde; in de tijd van Aristarchus dacht men nog dat ook de Zon om de Aarde draaide.

Verder trekken we $AM$ door tot aan de zijde $EF$ van het vierkant en bepalen we de snijpunten $D$ en $H$ met de boog en de zijde. NB: de hoek $\angle AZM$ is in het plaatje groter dan $3^{\rm o}$ omdat de echte hoek te klein is voor een duidelijke tekening. De punten $D$ en $H$, en ook $A$ en $M$, zouden bijvoorbeeld vrijwel samenvallen.

We trekken de diagonaal $AF$, dan is $\angle EAF$ een halve rechte hoek. We trekken ook de bissectrice $AG$ van deze hoek, dan is $\angle EAG$ dus een kwart van een rechte hoek.

Nu kunnen we wat conclusies gaan trekken. Omdat $\angle AMZ$ een rechte hoek is, en samen met $\angle EAD$ ook volgt dat $\angle EAD$ ook ééndertigste van een rechte hoek is. Hieruit volgt dat de verhouding $\angle EAG : \angle EAD$ gelijk is aan $15 : 2$. Het argument van Aristarchus: verdeel de rechte hoek in zestig gelijke delen, bestaat $\angle EAG$ uit $15$ delen en $\angle EAD$ uit $2$ delen.

De volgende conclusie is een ongelijkheid: de verhouding $GE : HE$ is groter dan de verhouding $\angle EAG : \angle EAD$ en dus geldt $GE : HE > 15 : 2$. Daar zit een stelling achter die Aristarchus al eerder had bewezen. We komen daar later op terug, maar we maken eerst de afschattingen af.

Omdat $AF$ de diagonaal van het vierkant op $AE$ is geldt $AF^2 = 2AE^2$. Omdat $AG$ de bissectrice van $\angle EAF$ is geldt volgens de Bissectricestelling dat $AF : AE = GF : GE$, dus geldt ook $FG^2 = 2GE^2$. Nu geldt dat $49 = 7^2$ kleiner is dan $2 \cdot 25 = 2 · 5^2$ en dus is de verhouding $FG : GE$ groter dan $7 : 5$.

Maar dan is de verhouding $(FG + GE) : GE$ groter dan $(7 + 5) : 5$ en dat is $12 : 5$. Die verhouding is ook gelijk aan $36 : 15$. Nu combineren we de verhoudingen en we vinden dat $FE : HE$ groter is dan $36 : 2$ en dat is dus gelijk aan $18 : 1$.

Nu zijn we er bijna: $AH$ is iets groter dan $AD$ en $AD$ is gelijk aan $AE$ en dus ook aan $FE$. Conclusie:

$$AH : HE > FE : HE > 18 : 1$$

De driehoeken $AMZ$ en $HEA$ zijn gelijkvormig, dus $AZ : AM = HA : HE$ en we vinden dat $AZ : AM$ groter is dan $18 : 1$.

Kleiner dan 20

We maken nu figuur 3. 

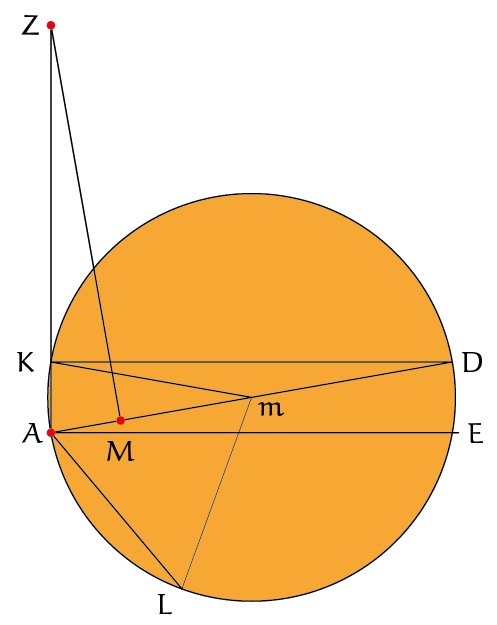
We beginnen weer met de driehoek $AMZ$, en we nemen de punten $D$ en $E$ uit de vorige figuur mee. Dus $AZ = AD = AE$, en $\angle EAD = \angle AZM = 3^{\rm o}$.

Trek de loodlijn uit $D$ op $AZ$ en noem het snijpunt $K$. Omdat $DK$ en $AE$ parallel zijn geldt $\angle ADK = \angle EAD$.

Trek nu de cirkel door $A$, $D$, en $K$, met middelpunt $m$. Dan is $AD$ een diameter van de cirkel omdat de hoek $\angle AKD$ recht is (stelling van Thales).

Driehoek $mKD$ is gelijkbenig, dus $\angle mKD = \angle mDK = \angle ADK$; we vinden dat $\angle KmD + 2\angle ADK = 180^{\rm o}$. Maar ook geldt $\angle KmD +\angle AmK = 180^{\rm o}$, en dus $\angle AmK = 2\angle ADK$. Daaruit volgt dat $\angle AmK$ gelijk is aan twee-dertigste van een rechte hoek, en de boog $AK$ is dan één-zestigste van de hele cirkel.

Ten slotte nemen we $L$ op de cirkel zó dat $AmL$ een gelijkzijdige driehoek is, met $AL = mA = mL$ dus. Dan is $\angle AmL$ zestig graden groot.

De boog $AL$ is dus één-zesde van de cirkel en daarmee gelijk aan $10$ maal de boog $AK$. Nu komt er weer een ongelijkheid: de verhouding van de bogen $AL$ en $AK$ is groter dan de verhouding van de lijnstukken $AL$ en $AK$ (hier komen we straks ook op terug). Dus het lijnstuk $AL$ is kleiner dan $10$ keer het lijnstuk $AK$. 

Maar $AD = 2 \cdot mA = 2 \cdot AL$, dus $AD$ is kleiner dan $20$ keer het lijnstuk $AK$. 

Nu merken we op dat de driehoeken $AMZ$ en $AKD$ gelijkvormig zijn. Dus volgt dat $AZ$ kleiner is dan $20$ keer het lijnstuk $AM$.

Dat geeft ons dus de tweede afschatting.

De gebruikte stellingen

We lopen de stellingen na die Aristarchus gebruikt heeft. Eerst de ongelijkheden en dan de bissectricestelling.

We laten hier zien hoe je die ongelijkheden met behulp van goniofuncties kunt bewijzen. In een later artikel zullen we zien hoe Aristarchus het zelf deed, helemaal meetkundig.

Ongelijkheid 1

We nemen het belangrijkste stuk uit de eerste grote figuur over.

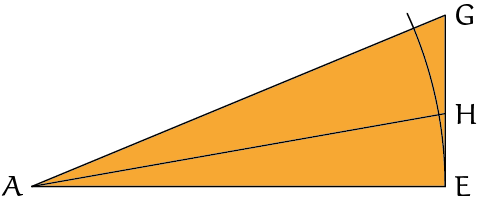
De eerste ongelijkheid die Aristarchus gebruikte zegt dat $EG : EH$ groter is dan de verhouding $\angle EAG:\angle EAH$.

Nu bekijken we de figuur met moderne ogen. Dan zien we daarin twee tangensen staan: $\tan(\angle EAG)=\frac{EG}{AE}$ en $\tan(\angle EAH)=\frac{EH}{AE}$.

We kunnen dan concluderen dat de ongelijkheid het volgende zegt:

$$\frac{\tan(\angle EAG)}{\tan(\angle EAH)}=\frac{EG}{EH}>\frac{\angle EAG}{\angle EAH}$$

Als we $\alpha = \angle EAG$ en $\beta = \angle EAH$ schrijven dan staat er, iets overzichtelijker: als $0 < \beta < \alpha < $\frac{\pi}{2}$ dan geldt

$$\frac{\tan(\alpha)}{\tan(\beta)}>\frac{\alpha}{\beta}$$

of, na kruislings vermenigvuldigen:

$$\frac{\tan(\alpha)}{\alpha}>\frac{\tan(\beta)}{\beta}.$$

Opgave 1 Bewijs deze ongelijkheid met behulp van de afgeleide. Opgave 2 Neem nu $\alpha = \angle EAG =\frac{\pi}{8}$ en $\beta=\angle EAH=\frac{\pi}{60}$ en probeer de afschatting van Aristarchus langs deze weg af te leiden. Gebruik gonioformules om $\tan\left(\frac{\pi}{8}\right)$ exact te bepalen.

Ongelijkheid 2

We nemen weer de belangrijkste punten uit de tweede grote figuur over.

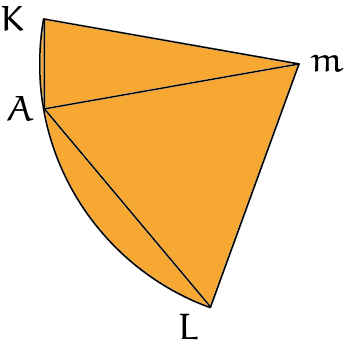
Aristarchus gebruikte dus dat de verhouding van de bogen $AL$ en $AK$ groter is dan de verhouding van de koorden $AL$ en $AK$.

Net als bij ongelijkheid 1 kun je deze ongelijkheid met moderne ogen bekijken. Als we de straal van de cirkel even op $1$ zetten dan kunnen we de koorden $AK$ en $AL$ met behulp van sinussen uitdrukken:

$AK=2\sin\left(\tfrac{1}{2}\angle AmK\right)$ en $AL = 2\sin\left(\tfrac{1}{2}\angle AmL\right).$

Schrijf nu $\beta = \tfrac{1}{2}\angle AmK$ en $AL = 2\sin\left(\tfrac{1}{2}\angle AmL\right)$, dan geldt $0 < \beta < \alpha < \frac{\pi}{2}$ en de ongelijkheid wordt

$$\frac{\alpha}{\beta}=\frac{\tfrac{1}{2}{\rm boog}AL}{\tfrac{1}{2}{\rm boog}AK}>\frac{\tfrac{1}{2}AL}{\tfrac{1}{2}AK}=\frac{\sin(\alpha)}{\sin(\beta)}$$

of, na kruislings vermenigvuldigen:

$$\frac{\sin(\alpha)}{\alpha}<\frac{\sin(\beta)}{\beta}.$$ 

Opgave 3 Bewijs deze ongelijkheid met behulp van de afgeleide. Opgave 4 Neem nu $\alpha = \tfrac{1}{2}\angle AmL = \frac{\pi}{6}$ en $\beta=\tfrac{1}{2}\angle AmK = \frac{\pi}{60}$ en probeer de afschatting van Aristarchus langs deze weg af te leiden.

De bisseCtriCestelling

De bissectricestelling zegt dat in een driehoek $ABC$, met bissectrice $AD$ vanuit $A$ de verhoudingen $AB : AC$ en $DB : DC$ aan elkaar gelijk zijn (teken zelf een plaatje). In ons speciale geval kunnen we ook rechtstreeks inzien wat de nodig hebben, namelijk dat in onze figuur $FG^2 = 2GE^2$ geldt.

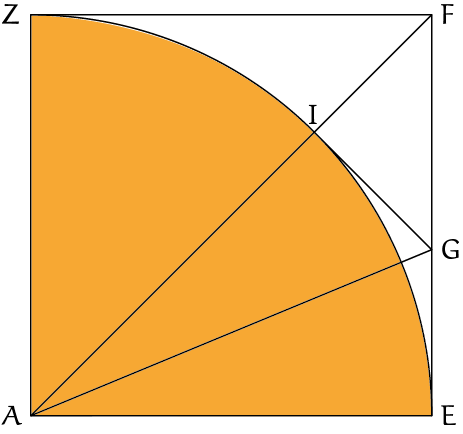
Teken het snijpunt $I$ van de lijn $AF$ en de boog $EZ$. Dan geldt $AI = AE$, en $AI$ en $AE$ liggen gespiegeld ten opzichte van de bissectrice. Maar dan liggen de raaklijnen aan de kwartcirkel in $E$ en $I$ ook gespiegeld ten opzichte van $AG$ en daarom snijden ze elkaar in $G$. De conclusie is dat $IG = GE$.

In de driehoek $GIF$ geldt $FG^2 = 2IG^2$, en dus volgt $FG^2 = 2GE^2$.

Hoe goed zijn de afsChattingen?

Als je opzoekt wat de werkelijke afstanden Aarde – Zon en Aarde – Maan zijn zul je zien dat Aristarchus er erg naast zat met zijn $18$ en $20$.

De afstand Aarde – Zon is, afgerond, zo'n $150$ miljoen kilometer, en de afstand Aarde – Maan is, ook afgerond, $384\ 000$ kilometer. Als je die op elkaar deelt krijg je $391$ (weer afgerond). Dat ligt tussen $360$ en $400$, Aristarchus zat er dus een factor $20$ naast.

Waar die factor vandaan komt is achteraf wel duidelijk. Aristarchus kon niet zo nauwkeurig meten als tegenwoordig. In november 2024 stond in NRC een artikel waarin voor de hoek $\angle ZAM$ de waarde $89{,}85^{\rm o}$ werd gegeven, onze hoek $\varphi$ is daarmee $0{,}15^{\rm o}$ groot. En $1/\sin(0{,}15^{\rm o})$ is ongeveer gelijk aan $382$ en dat komt al meer in de buurt.