Bijlagen

De bijlagen bevatten afleidingen van enkele hierboven vermelde formules en getallen. De schrijfwijze kan echter wat afwijken.

Coördinaten van tetraëders

We gaan even terug naar het voorschrift voor tetraëders:

Plaats een nieuwe punt midden in het lichaam, verbind die met alle hoekpunten, en verplaats dit punt in de richting van de nieuwe dimensie totdat alle lijnen even lang zijn.

Het ‘punt midden in het lichaam’ is natuurlijk het zwaartepunt, het geometrisch middelpunt. Vanaf dit punt maken we een lijn in de richting van de nieuwe dimensie, de hoogtelijn. Zie de figuur.

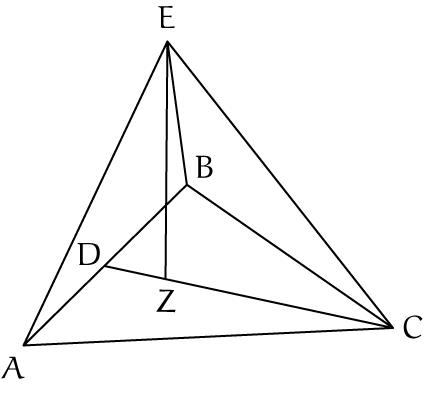
$ABC$ is (schematisch) een $n$-dimensionale tetraëder. $C$ is het laatst toegevoegde punt en $CD$ de hoogtelijn $h_n$. $Z$ is het zwaartepunt. De positie daarvan is afhankelijk van het aantal hoekpunten, in dit geval $n+1$. Er geldt dan $DZ : ZC = 1 : n$, zodat $ZC = \frac{n}{n+1} \times h_n$. Op dit punt wordt een lijn geplaatst in de richting van de nieuwe dimensie, $ZE = h_{n+1}$, zodanig dat de lijn $EC$ (en andere) de correcte ribbelengte $r$ krijgt. Met Pythagoras: $ZC^2 + ZE^2 = EC^2$, ofwel:

$$\left(\frac{n}{n+1} \times h_n\right)^2 + h_{n+1}^2 = r^2.$$

Hiermee zijn de coördinaten in tabel 5 berekend uitgaande van $h_1 = r = 2$, waarbij evenwel alle punten zo zijn verschoven in de richting van de nieuwe dimensie dat het zwaartepunt steeds in de oorsprong ligt. Deze operatie lijkt mogelijk nogal gekunsteld, maar controleberekeningen laten zien dat de afstand van elk tweetal punten in tabel 5 inderdaad exact gelijk is aan $2$, de ribbelengte.

Verder volgt dat: $h_n = r  \times \sqrt{\frac{n+1}{2n}}$.

De coördinaten in tabel 5, met ribbelengte $2$, kunnen we als volgt uitdrukken:

voor de $n$-de coördinaat ($1=x_1, 2=x_2$ enz) van punt $i$ geldt:

$\begin{matrix}
C_{n,i} = & -a & i = 1 \ldots n \\ 
 & na & i = n+1 \\ 
 & 0 & i > n+1 
\end{matrix}$

$a = \sqrt{\frac{2}{n\cdot(n+1)}}$.

Bedenk ook dat de coördinaten sterk afhankelijk zijn van de oriëntatie van het object. Daarvoor zijn er geen afspraken en ze kunnen dus in verschillende bronnen verschillend zijn.

Volumes van octaëders en tetraëders.

Zowel meer-dimensionale octaëders als tetraëders worden in feite gemaakt door het maken van piramides, zie de instructies in het voorgaande. Het volume van een piramide is in het algemeen:

$$volume = \mbox{'}afmeting\ grondvlak\mbox{'} \times \frac{hoogte}{aantal\ dimensies}$$

dus voor $2$ dimensies (driehoek): $halve\ basis \times hoogte$, en voor $3$ dimensies (piramide): $\tfrac{1}{3} grondvlak \times hoogte$, zoals bekend verondersteld. In het algemeen is ‘$afmeting\ grondvlak$’ het ‘$volume$’ van het $n-1$ dimensionale object.

$Octa\ddot{e}der$

Beschouw nu een octaëder met ribbe lengte $1$ (diagonaal lengte $\sqrt 2$). We gaan hier een dimensie aan toevoegen door er twee piramides op te zetten, ieder met hoogte $\tfrac{1}{2}\sqrt{2}$ (halve diagonaallengte). We krijgen dan de recurrente betrekking:

$$V_n = 2V_{n-1} \frac{h_n}{n} = 2 V_{n-1} \tfrac{1}{2}\frac{\sqrt{2}}{n} = V_{n-1} \frac{\sqrt{2}}{n}.$$

Er van uitgaande dat $V_1 = \sqrt{2}$ (diagonaallengte, figuur 6) levert dat op:

$$V_n=\frac{\sqrt{2^n}}{n!}$$

Gecheckt: $V_2 = 1, V_3 = \frac{\sqrt{2}}{3}, V_4 = \tfrac16$.

$Tetra\ddot{e}der$

Een tetraëder is lastiger omdat de hoogte niet zo simpel is. Uit tabel 5 kan worden afgeleid dat voor een tetraëder met ribbe lengte $2$ de hoogte gelijk is aan: $h_n = \frac{n+1}{\sqrt{\frac{n(n+1)}{2}}}$. Voor een tetraëder met ribbelengte $1$ is dat de helft en dat levert op:

$$h_n = \sqrt{\frac{n+1}{2n}}.$$

Gecheckt:  $h_2 = \tfrac12\sqrt3, h_3 = \sqrt{\frac23}$.

 

Bij elke nieuwe dimensie wordt slechts één piramide toegevoegd. Dat levert de recurrente betrekking:

$$V_n = V_{n-1} \frac{h_n}{n}  = V_{n-1} \frac{\sqrt{\frac{n+1}{2n}}}{n} = V_{n-1}\tfrac1n\sqrt2\sqrt{\frac{n+1}{n}}.$$

Er van uitgaande van $V_1 = 1$ (ribbelengte, figuur 7) levert dat op:

$$V_n=\sqrt{\frac{n+1}{\sqrt{2^n}n!}}.$$

Gecheckt: $V_2 = \tfrac14\sqrt3, V_3 = \frac{\sqrt2}{12}, V_4 = \frac{\sqrt5}{96}$.

Afleiding van de reCurrente betrekking voor bolvolumes.

We hebben reeds gevonden: $V_n = V_{n-1} F_{n-1} = V_{n-2} F_{n-2}F_{n-1}$.

met $F_n = \frac{2^{n+1}}{(n+1)!}\left\{\Gamma\left(\frac{n}{2}+1\right)\right\}^2$.

We gebruiken nu een waarschijnlijk onbekend begrip: dubbelfaculteit:

$n!! = n\cdot(n-2)\cdot(n-4)\cdots$, met $1$ of $2$ als laatste factor,

dus bijvoorbeeld $7!! = 7\cdot 5\cdot 3\cdot 1 = 105$.

Het is makkelijk na te gaan dat:  $n!! \cdot (n-1)!! = n!$.

Ook geldt dat voor even waarden van $n$, $n = 2a$:  $n!! = a! \cdot 2^a = (n/2)!\cdot2^{n/2}.$

Voor oneven waarden van $n$, $n=2a+1$ geldt: $n!! = \frac{n!}{(2a)!!} = \frac{n!}{(a! \cdot 2^a)}$.

Deze uitdrukkingen hebben we zo meteen nodig.

Wat is nu $\Gamma\left(\frac{n}{2}+1\right)$?

Als $n$ even is, $n = 2a$ dan: $\Gamma\left(\frac{n}{2}+1\right) = \Gamma(a+1) = a! = \frac{n!!}{2^{n/2}}$.  

Als $n$ oneven is: $\Gamma\left(\frac{n}{2}+1\right) = \tfrac{n}{2} \cdot\frac{n-2}{2} \cdot \frac{n-4}{2} \cdot \cdots \cdot \tfrac12 \cdot \Gamma\left(\tfrac12\right)$; $\Gamma\left(\tfrac12\right)=\sqrt{\pi}$.

dus: $\Gamma\left(\frac{n}{2}+1\right) = \frac{n!!}{2^{(n+1)/2}}\cdot\sqrt\pi$.

Definieer nu gemakshalve $G_n = \Gamma\left(\frac{n}{2}+1\right)$. We hebben nu nodig $G_{n-1}\cdot G_{n-2}$.

Als $n$ even is:

$\begin{matrix} 
G_{n-1} & = & \frac{(n-1)!!}{2^{n/2}}\cdot\sqrt\pi& &\\ 
G_{n-2} & = & \frac{(n-2)!!}{2^{(n-2)/2}} & & \\ 
G_{n-1}\cdot G_{n-2} & = & \frac{(n-1)!! \cdot (n-2)!!}{2^{n-2}}\cdot\sqrt\pi &=& \frac{(n-1)!}{2^{n-1}}\cdot\sqrt\pi 
\end{matrix}$

Als $n$ oneven is:

$\begin{matrix}
G_{n-1}&=&\frac{(n-1)!!}{2^{(n-1)/2}}& &\\
G_{n-2}&=&\frac{(n-2)!!}{2^{(n-2)/2}}\cdot\sqrt\pi& &\\
G_{n-1}\cdot G_{n-2}&=&\frac{(n-1)!!\cdot(n-2)!!}{2^{n-1}}\cdot\sqrt\pi &= \frac{(n-1)!}{2^{n-1}}\cdot\sqrt\pi
\end{matrix}$

Dus de waarde van $G_{n-1}\cdot G_{n-2}$ is voor even en oneven $n$ hetzelfde.

We krijgen nu:

$\begin{matrix}
F_{n-1}\cdot F_{n-2}&=&\frac{2^n}{n!}\cdot\frac{2^{n-1}}{(n-1)!}\cdot\left(G_{n-1}\cdot G_{n-2}\right)^2 & =& \\
&=&\frac{2^n}{n!}\cdot\frac{2^{n-1}}{(n-1)!}\cdot\frac{(n-1)!}{2^{n-1}}\cdot\frac{(n-1)!}{2^{n-1}}\cdot\pi&=&\frac{2\pi}{n}
\end{matrix}$

Uiteindelijk leidt dit dus tot:

$V_n=V_{n-2}\cdot\frac{2\pi}{n}.\ \ \ \ \ \ \mbox{ Q.E.D.}$

Hieruit kunnen ook eenvoudig expliciete uitdrukkingen voor $V_n$ worden afgeleid:

$\begin{matrix}
n=2a:&\ \ &V_n=\frac{\pi^a}{a!}& & & &\\
n=2a+1:&\ \ &V_n=\frac{2^{a+1}\cdot\pi^a}{n!!}&=&\frac{2^{2a+1}\cdot\pi^a\cdot a!}{n!}&=&\frac{2^n\cdot\pi^a\cdot a!}{n!}
\end{matrix}$