In 1904 schreef de Zweedse wiskundige Helge von Koch een artikel met de welluidende titel Sur une courbe continue sans tangente obtenue par une construction géométrique élémentaire. Wie wat Frans kent weet nu waar het artikel over gaat; maar de titel vertelt niet het hele verhaal. In de inleiding schreef Von Koch waarom hij "op elementaire meetkundige wijze een kromme zonder raaklijnen" wilde construeren. In 1875 had de Duitse wiskundige Karl Weierstrass namelijk een  voorbeeld gemaakt van een continue functie die in geen enkel punt differentieerbaar is. Die functie wordt gegeven door

$$f(x)=\sum_{k=0}^{\infty}a^k\cos(b^k\pi x).$$

Hierin is $a$ een reëel getal in het open interval $(0,1)$ en $b$ een oneven natuurlijk getal groter dan $1$; samen voldoen $a$ en $b$ nog aan

$$ab > 1+\frac{3\pi}{2}.$$

Zoals Von Koch opmerkte dachten de meeste wiskundigen tot dan toe dat elke kromme overal een raaklijn heeft, op misschien in een paar uitzonderlijke punten na. Immers, als je zelf een 'willekeurige' kromme tekent zitten er misschien wat knikken
en keerpunten in, maar verder is hij meestal wel mooi glad, zoals in figuur 1.

Figuur 1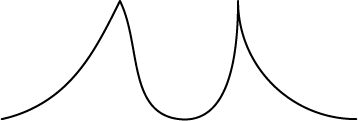

 De grafiek van de functie van Weierstrass is een kromme die in geen enkel punt een raaklijn heeft, en deze haalt die oude gedachte dus grondig onderuit. Maar, schreef Von Koch, die functie van Weierstrass komt uit de Analyse en je ziet eigenlijk niet goed waarom er geen raaklijnen zijn, anders dan door netjes met de definitie van de afgeleide te werken en te laten zien dat

$$\lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h}$$

voor geen enkele $a$ bestaat.

Hij had zich daarom afgevraagd of dit niet wat eenvoudiger kon: een kromme maken waarvan het "intuïtief" duidelijk is dat deze geen raaklijnen heeft. En hij dacht dat hij daar in geslaagd was. Laten we maar eens kijken.

De Kromme

We beginnen met de lijn $AB$ in het vlak (figuur 2).

Figuur 2

 Verdeel de lijn in drie gelijke stukken: $AC$, $CE$, en $EB$, en zet op $CE$ een gelijkzijdige driehoek $CDE$. Zo komen we tot figuur 3.

Figuur 3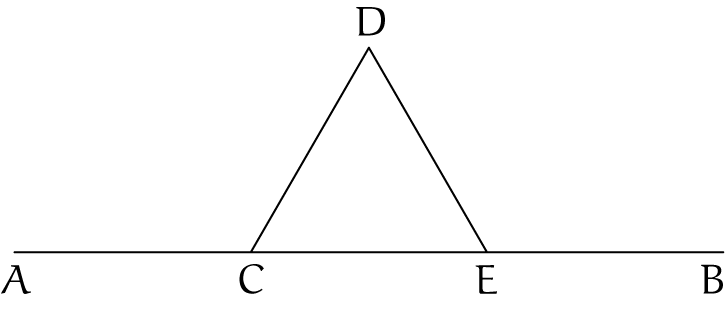

 Von Koch noemde dit "het toepassen van operatie $\Omega$ op het lijnstuk $AB$". 

De volgende stap is het toepassen van operatie $\Omega$ op elk van de vier lijnstukken $AC$, $CD$, $DE$, en $EB$. 

Dat geeft ons zestien lijnstukjes: $AF$, $FG$, enzovoort in figuur 4.

Figuur 4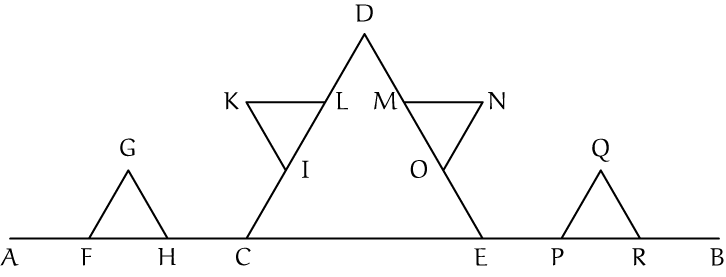

 Op elk van die zestien lijnstukjes passen we weer de operatie $\Omega$ toe; dat geeft ons $4^3 = 64$ lijnstukjes $AS$, $ST$, enzovoort. 

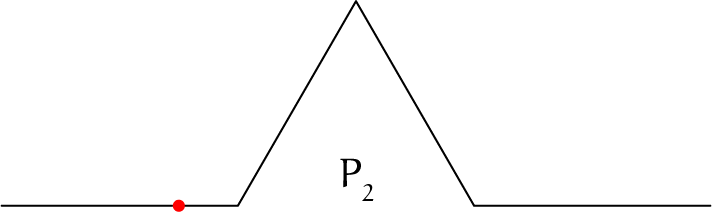
Helge von Koch tekende op een gegeven moment niet alles meer want dat zou met potlood en liniaal een heel gedoe zijn. Aan het eind laat ik de tekening zien die in het artikel van Von Koch te bewonderen is. De tekeningen kloppen niet helemaal want er staan eigenlijk een heleboel gebroken lijnen over elkaar heen getekend. De eerste is de lijn $AB$, die noemde Von Koch kortweg $P_1$. De tweede, $P_2$, is dan $ACDEB$, die bestaat uit vier lijnstukken. In figuur 3 zijn $P_1$ en $P_2$ samen getekend.

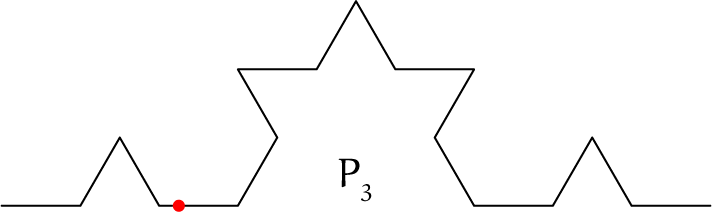
Vervolgens kunnen we de derde nog opschrijven: $P_3$ is dan 

$$AFGHCIKLDMNOEPQRB,$$

met zestien lijnstukken. De gebroken lijnen $P_1$, $P_2$ en $P_3$ staan bij elkaar in figuur 4.

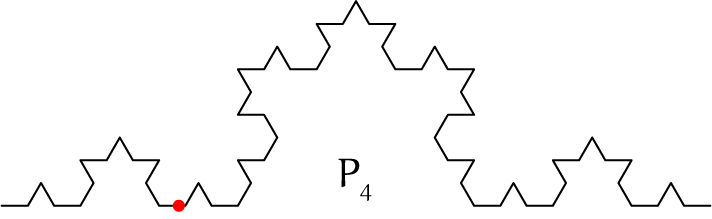
Elke volgende gebroken lijn, $P_{n+1}$, ontstaat door op alle lijnstukken van $P_n$ de operatie $\Omega$ toe te passen; $P_{n+1}$ bestaat dan dus uit $4^n$ even lange lijnstukjes.

In de grote tekening in figuur 7 zien we $P_1$, $P_2$ en $P_3$ helemaal en van $P_4$ en $P_5$ alleen beginstukken.

Beter is het de $P_n$ afzonderlijk te tekenen (figuur 5).

Figuur 5

In de rest van het artikel bewees Von Koch dat de rij $P_1, P_2, P_3, \dots, P_n, \dots$ naar een kromme $P$ convergeert en dat die limietkromme in geen enkel punt een raaklijn heeft.

Raaklijnen

Wat is een raaklijn eigenlijk? Dat werd door Von Koch ook netjes gedefinieerd. Trek voor elk tweetal punten op de kromme de lijn door die twee punten. Neem een punt $x$ vast en laat een punt $y$ op de kromme naar $x$ bewegen. Als de verbindingslijn door $x$ en $y$ naar een vaste lijn convergeert is die vaste lijn per definitie de raaklijn in $x$. Dat laatste gaat in elk punt van de limietkromme $P$ mis.

Hiervoor merken we eerst even op dat de knikpunten van de krommen $P_n$ op de limietkromme $P$ moeten liggen. Zo liggen $A$, $C$, $E$ en $B$ op alle $P_n$, dus op $P$. De punten $I$, $L$, $D$, $M$ en $O$ liggen op alle $P_n$ vanaf $n = 2$, dus op $P$. En $G$, $K$, $N$ en $Q$ doen vanaf $n = 3$ altijd mee. We laten eerst zien waarom het in al die knikpunten mis gaat. Kijk maar eens bij $C$. Als je van links naar $C$ gaat met een variabel punt kom je telkens weer op de
$x$-as terecht, en ook op de verbindingslijn van $C$ en $G$. 

Kijk maar in figuur 6.

Figuur 6

Dit betekent dat de verbindingslijn heen en weer blijft slingeren tussen twee vaste lijnen, de rode en de blauwe, en dus niet naar een vaste lijn convergeert. En aan de andere kant gebeurt precies hetzelfde. Een dergelijk argument kun je ook voor punten als $D$, $K$ en $N$ gebruiken. 

Dit bedoelde Helge von Koch misschien met de opmerking dat het ‘intuïtief’ duidelijk zou moeten zijn dat de kromme in geen enkel punt een raaklijn heeft. Maar als je het artikel leest zie je dat hij toch wel een paar pagina’s met het bewijs bezig is. Er zijn namelijk punten op $P$ waar het allemaal niet zo duidelijk is. Als we bijvoorbeeld $A$ in de oorsprong leggen en $B$ in $(1,0)$ dan kun je narekenen dat $(\frac14,0)$ op alle krommen ligt maar nooit een knikpunt wordt; kijk maar in de plaatjes van $P_1$ tot en met $P_4$: het rode stipje wijst het punt $(\frac14,0)$ aan.

Dat ligt telkens net naast het volgende driehoekje dat door operatie $\Omega$ gevormd wordt. Voor zo’n punt moet je wat subtieler redeneren. En dan is er nog het geval dat je een punt op $P$ hebt dat op geen enkele $P_n$ ligt; dan moet je de constructie nog nauwkeuriger bekijken om in te zien dat er geen raaklijn in dat punt is.

Figuur 7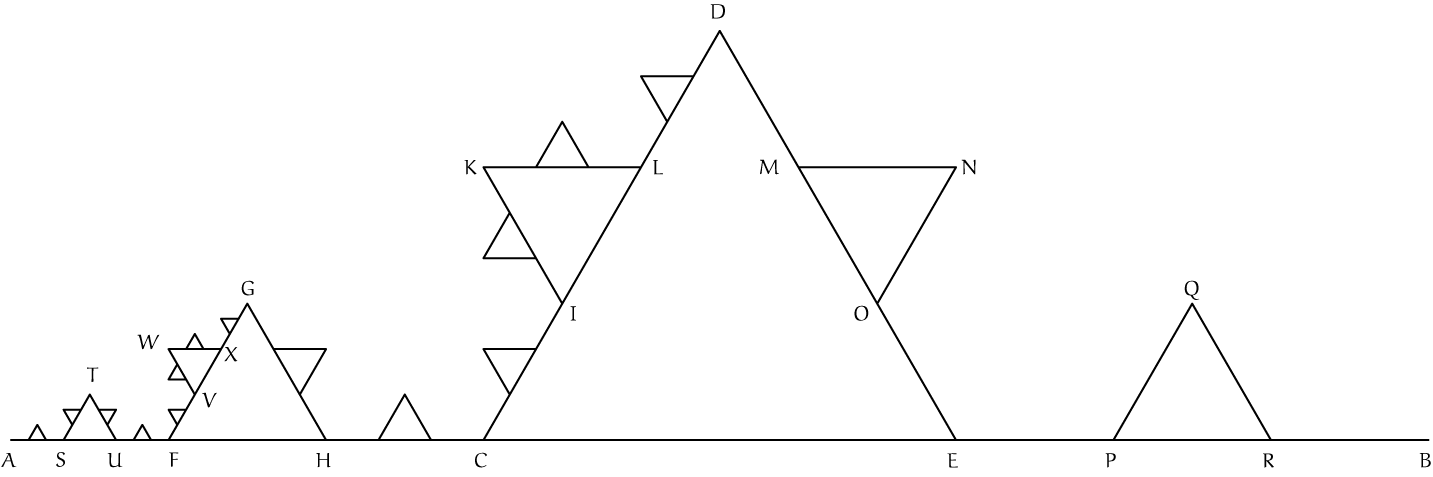 De tekening uit het artikel van Helge von Koch

Het punt (1/4, 0)

Als je naar de plaatjes van  $P_2$, $P_3$ en $P_4$ kijkt zie je dat het punt $(\frac14,0)$ eerst links, dan rechts, en dat weer links van het nieuwste driehoekje ligt. Dat gaat zo door: links als $n$ even is en rechts als $n$ oneven is.

Dit heeft te maken met het drietallig stelsel: er geldt namelijk
$$\frac14=0\cdot3^{-1}+2\cdot3^{-2}+0\cdot3^{-3}+2\cdot3^{-4}+\cdots$$
(reken maar na met behulp van een meetkundige reeks). Als we van $P_n$ naar $P_{n+1}$ gaat vertelt het getal bij $3^{-n}$ ons waar het getal ligt ten opzichte van het nieuwe driehoekje: links bij $0$ en rechts bij $2$.

Hoe helpt on dit? Als we in $(\frac14,0)$ de verbindingslijnen met andere punten op $P$ trekken dat komen we altijd punten op de $x$-as tegen (knikpunten bijvoorbeeld) en toppen van de driehoekjes links en rechts van ons punt. En daar gebeurt dus iets als in figuur 8.

Figuur 8 of

De absolute waarde van de helling van de verbindingslijn van $(\frac14,0)$ met de dichtstbijzijnde top is altijd groter dat die van de blauwe lijn (en die is $\frac13\sqrt3$) en kleiner dan die van de zijde van het driehoekje (en die is $\frac12\sqrt3$), en beurtelings stijgend en dalend. De hellingen van die verbindingslijnen zijn dus om en om groter dan $\frac13\sqrt3$ en kleiner dan $-\frac13\sqrt3$. Dat betekent dat de verbindinslijnen niet naar een vaste (raak)lijn gaan. 

Opgave 1 Laat zien dat de helling van de blauwe lijnen inderdaad $\frac13\sqrt3$ is.

De volgende opgave is niet eenvoudig; het helpt als je eerst wat informatie
over de Cantorverzameling opzoekt.

Opgave 2 Bewijs dat als een punt van de vorm $(t,0)$ op $P_1$ geen knikpunt is en tijdens de hele constructie op de $x$-as blijft er geldt dat $$t=a_1\cdot3^{-1}+a_2\cdot3^{-2}+\cdots+a_n\cdot3^{-1}+\cdots$$ waarbij de $a_i$ gelijk zijn aan $0$ of $2$ en waarbij de waarden $0$ en $2$ oneindig vaak voorkomen.

Met behulp van deze opgave kun je laten zien dat in elk punt van $P$ dat al op een $P_n$ ligt geen raaklijn bestaat.

Punten die op géén P_n liggen

Wat betekent het dat een punt wel op $P$ ligt maar niet op een $P_n$. Daar zat voor Von Koch het meeste werk aan.

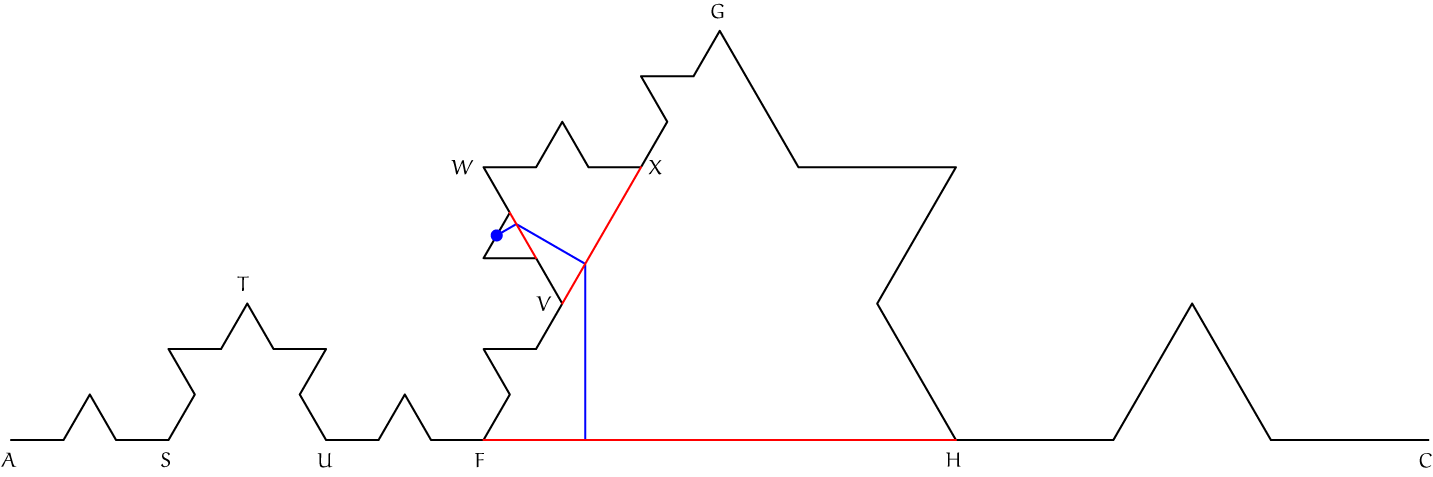
We gaan het bewijs niet helemaal uitschrijven maar aan de hand van de tekening van Von Koch zelf laten we zien wat er gebeurt. We bekijken alleen het stuk tussen $A$ en $C$.

Figuur 9 De tekening uit het artikel van Helge von Koch

Het blauwe punt ligt nu op $P_5$ maar in latere stappen wordt het weer opgetild.  Het begon als een punt tussen $F$ en $H$, ging omhoog naar een punt tussen $V$ en $X$, en ging weer 'omhoog' naar een punt tussen de twee (naamloze) knikpunten tussen $V$ en $W$, en toen weer 'omhoog'. 

Telkens als het punt 'omhoog' gaat onthouden we de uiteinden van het lijnstuk waar het op lag. We hebben dus al de paren $(F,H)$ en $(V,X)$ en het naamloze paar. Die uiteinden convergeren mee naar een punt op $P$ dat dus op géén $P_n$ ligt. Hun verbindingslijnen zouden dan naar de raaklijn in dat punt moeten convergeren. Maar dat lukt niet: elk tweetal opvolgende verbindingslijnen maakt een hoek van $\frac\pi3$. Ze bewegen te wild om naar een vaste lijn te convergeren.