De ongelijkheden die Aristarchus in zijn afschattingen van de verhouding van de afstanden Aarde–Zon en Aarde–Maan nodig had gingen over verhoudingen tussen rechte lijnstukken en verhoudingen van hoeken.

De eerste ongelijkheid

De eerste ongelijkheid van Aristarchus zegt dat in het volgende plaatje de verhouding $EG : EH$ groter is dan de verhouding $\angle AEG : \angle EAH$.

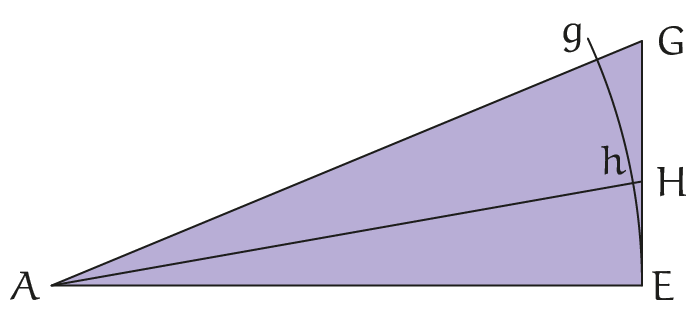
We kunnen de hoeken $\angle EAG$ en $\angle EAH$ vervangen door de bogen $Eg$ en $Eh$ omdat de verhoudingen $\angle EAG : \angle EAH$ en $Eg : Eh$ aan elkaar gelijk zijn. Dus de ongelijkheid zegt ook dat de verhouding $EG : EH$ groter is dan de verhouding $Eg : Eh$.

 

Opgave 1 Denk daar eens over na. Is dat makkelijk uit het plaatje af te lezen? Hoe zou je het zelf bewijzen?

 

Voor het bewijs maken we de figuur opnieuw, maar nu met een cirkelboog $PQ$ door $H$ getrokken.

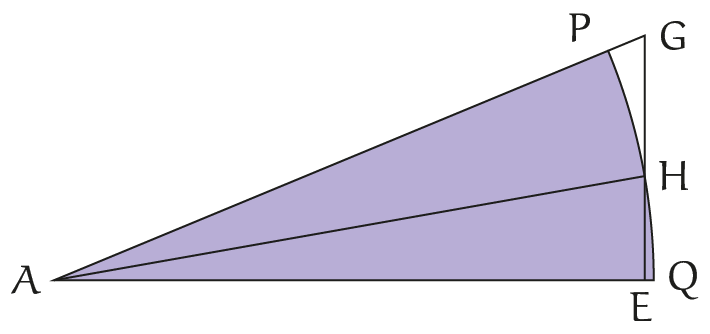
De cirkelsector $AHP$ is kleiner dan de driehoek $AHG$ en, net andersom, de cirkelsector $AQH$ is groter dan de driehoek $AEH$. Conclusie: de verhouding $\Delta AHG : \Delta AEH$ is groter dan de verhouding $($sector $AHP : ($sector $AQH)$ (immers, als $a > b$ en $c < d$, dan $\frac{a}{c}>\frac{b}{c}>\frac{b}{d}$).

Nu geldt: de oppervlakte van een cirkelsector is evenredig met de hoek, en de oppervlakte van een driehoek is evenredig met zijn basis.

We kunnen dus concluderen dat $($sector $AHP) : ($sector $AQH)$ gelijk is aan $\angle HAG : \angle EAH$ en $\Delta AHG : \Delta AEH = HG : EH$

Conclusie:

$HG : EH > \angle HAG : \angle EAH$.

Tel nu links en rechts $1$ bij de verhoudig op, links $EH : EH$ en rechts $\angle EAH : \angle EAH$, dan krijgen we

$1+\frac{HG}{EH} = \frac{EH + HG}{EH} = \frac{EG}{EH}$

en

$1+\frac{\angle HAG}{\angle EAH} = \frac{\angle EAH + \angle HAG}{\angle EAH}=\frac{\angle EAG}{\angle EAH}$

(we hebben voor de duidelijkheid en wegens de ruimte de verhoudingen als breuken opgeschreven).

We vinden wat we zochten:

$EG : EH > \angle EAG : \angle EAH$.

De tweede ongelijkheid

De tweede ongelijkheid van Aristarchus gaat over koorden en bogen in cirkels. In het volgende plaatje hebben we drie punten $A$, $K$ en $L$ op een cirkel met middelpunt $m$, en wel zó dat $\angle AmK$ kleiner is dan $\angle AmL$.

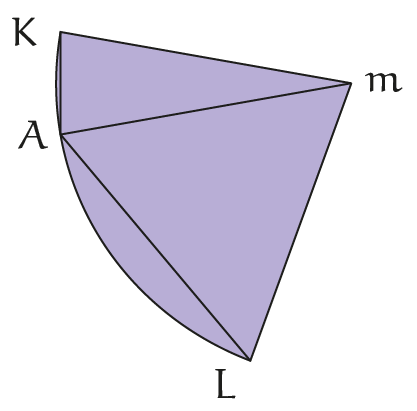
Dan geldt: de verhouding van de bogen $AL$ en $AK$ is groter dan de verhouding van de koorden $AL$ en $AK$.

Opgave 2 Denk hier, net als bij de eerste ongelijkheid, eens over na. Is dat makkelijk uit het plaatje af te lezen? Hoe zou je het zelf bewijzen?

 

De eerste verhouding, die van de bogen $AL$ en $AK$ is gelijk aan die van de hoeken $\angle AmL$ en $\angle AmK$.

We gaan dus bewijzen dat

$\angle AmL : \angle AmK > AL : AK$.

Voor het bewijs construeren we wat hulplijnen in de oorspronkelijke cirkel om $m$.

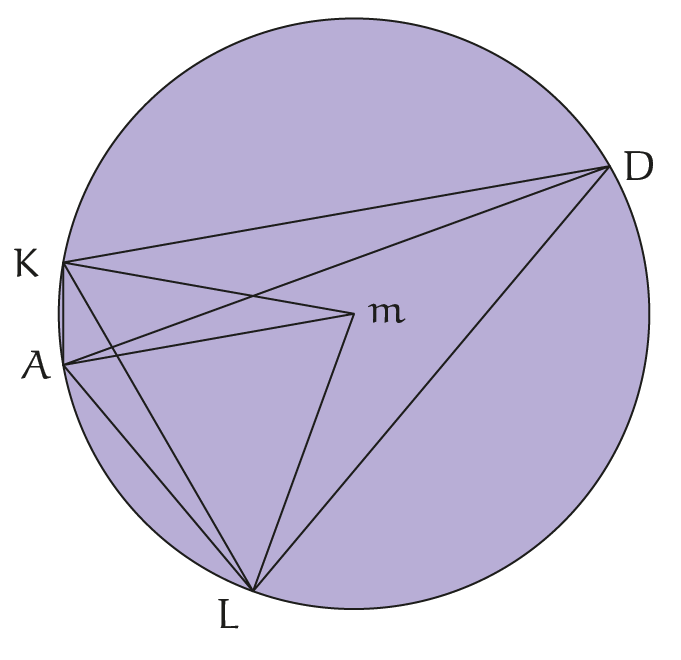
We trekken de bissectrice van de hoek $\angle LAK$ tot deze de cirkel snijdt in $D$. Wegens de stelling van de dubbele hoek weten we dat $\angle AmL = 2\angle ADL$ en $\angle AmK = 2\angle ADK$, zodat $\angle ADK < \angle ADL$ en ook $\angle AmL : \angle AmK = \angle ADL : \angle ADK$.

We gaan daarom bewijzen dat

$\angle ADL : \angle ADK > AL : AK$.

$(\star)$

 

We gebruiken de stelling van de dubbele hoek nog een keer: die geeft dat $\angle DmK = 2\angle DAK$ en $\angle DmL = 2\angle DAL$, maar $\angle DAK = \angle DAL$ en dus zijn de hoeken $\angle DmK$ en $\angle DmL$ ook gelijk. En daarom zijn de koorden van die hoeken, $DK$ en $DL$, even lang.

Trek nu ook het lijnstuk $LK$, het snijpunt met $AD$ noemen we E. In de gelijkbenige driehoek $\Delta KDL$ is de hoek $\angle KDE$ kleiner dan $\angle EDL$ (want $\angle KDE = \angle KDA < \angle ADL = \angle EDL$).

Dus lijnstuk $KE$ is kleiner dan $EL$. We trekken de loodlijn uit $D$ op $KL$, met snijpunt $F$. In de gelijkbenige driehoek $KDL$ hebben we dan $DF < DE < DK$.

Dus de cirkel met middelpunt $D$ en straal $DE$ snijdt de zijde $KD$ van de driehoek in $G$ en het verlengde van $DF$ in $H$.

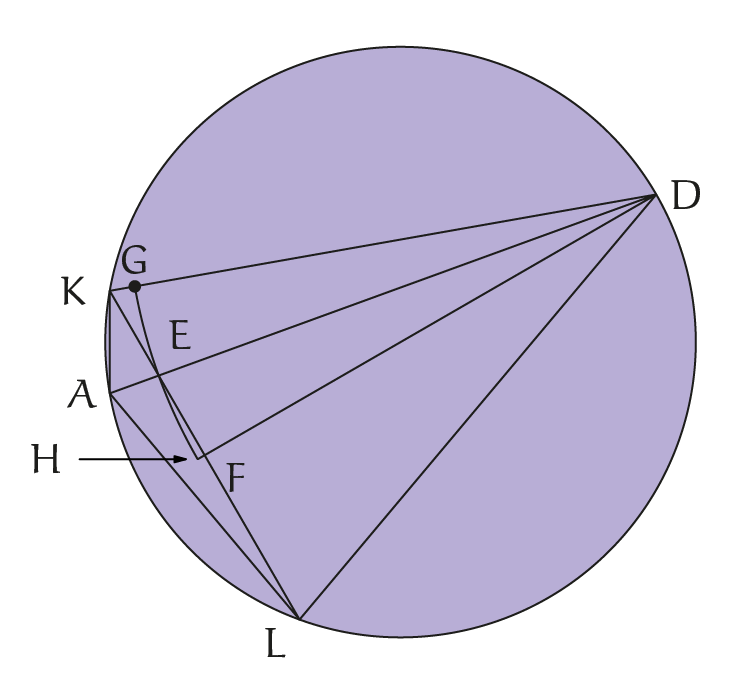
Nu kunnen we net als bij de eerste ongelijkheid weer sectoren en driehoeken vergelijken. Hier is sector $DEH$ groter dan $\Delta DEF$ en is sector $DEG$ kleiner dan $\Delta DEK$. We vinden dus

$\frac{{\rm sector }DEH}{{\rm sector} DEG}>\frac{\Delta DEF}{\Delta DEK}$.

Net als bij de eerste ongelijkheid kunnen we weer de driehoeken door hun bases vervangen en de sectoren door hun hoeken:

$\frac{\angle EDK}{\angle EDK} > \frac{EF}{EK}$.

We tellen weer links en rechts $1$ op, links $\frac{\angle EDK}{\angle EDK}$ en rechts $\frac{EK}{EK}$, met als resultaat

$\frac{\angle HDK}{\angle EDK} > \frac{FK}{EK}$.

Nu kunnen we de tellers verdubbelen:

$\frac{\angle LDK}{\angle EDK} > \frac{LK}{EK}$.

Nu trekken we weer $1$ af, links $\frac{\angle EDK}{\angle EDK}$ en rechts $\frac{EK}{EK}$, met als resultaten

$\frac{\angle LDK - \angle EDK}{\angle EDK} = \frac{\angle LDE}{\angle EDK}$.

en

$\frac{LK - EK}{EK} = \frac{LE}{EK}$.

zodat

$\frac{\angle LDE}{\angle EDK} > \frac{LE}{EK}$.

$(\dagger)$

 

Wat heeft dit met onze bogen en koorden te maken? Ten eerste: $\angle LDE = \angle ADL$ en $\angle EDK = \angle ADK$, dus de linkerverhouding in $(\dagger)$ is gelijk aan de linkerverhouding in $(\star)$.

Omdat $AE$ de bissectrice van de hoek $\angle KAL$ is volgt uit de bissectricestelling dat

$LA : AK = LE : EK$,

dus de rechterverhouding in $(\dagger)$ is gelijk aan de rechterverhouding in $(\star)$.

Gelijkheid $(\dagger)$ zegt dus precies hetzelfde als $(\star)$, en daarmee is $(\star)$ bewezen.

De bisseCtriCestelling

In het vorige artikel konden we de bissectricestelling vermijden omdat we haar alleen voor een speciale driehoek nodig hadden. We bekijken onze driehoek $AKL$ nog een keer en bewijzen de gelijkheid die we hierboven gevonden hebben: $LA : AK = LE : EK$.

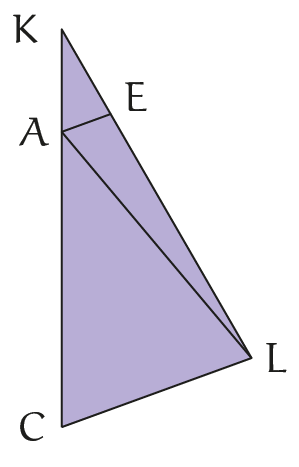
De lijn door $A$ en $K$ snijdt de lijn door $L$ die parallel is aan $EA$ in het punt $C$. Wegens Z-hoeken zijn de hoeken $\angle EAL$ en $\angle ALC$ gelijk, en omdat $EA$ en $LC$ parallel zijn, zijn $\angle KAE$ en $\angle ACL$ gelijk. Alle vier de hoeken zijn dus gelijk.

Dus $\Delta ACL$ is gelijkbenig en $AC = AL$. De driehoeken $KCL$ en $KAE$ zijn gelijkvormig dus geldt

$CK : AK = LK : EK$,

maar $KL = LE + EK$ en $CK = CA + AK$ dus deze verhoudingen kunnen we ook lezen als

$1+\frac{CA}{AK}$ en $1 + \frac{LE}{EK}$.

We zien dat $CA : AK = LE : EK$ maar $AC = AL$ en dus volgt

$LA : AK = LE : EK$.

De hoeken

Voor welke hoeken gelden de ongelijkheden eigenlijk?

In het plaatje van de eerste ongelijkheid kunnen de hoeken niet groter zijn dan een rechte hoek omdat alles zich in het eerste kwadrant afspeelt. 

Dat is ook te zien aan de moderne oplossing uit het vorige artikel die gebruikte dat $\frac{\tan(x)}{x}$ een stijgende functie is op het interval $\left[0,\tfrac{\pi}{2}\right)$.

Voor de tweede ongelijkheid is impliciet aangenomen dat de hoeken kleiner zijn dan gestrekte hoeken, of zoals Aristarchus zou zeggen: kleiner dan twee rechte hoeken.

Een koorde bepaalt namelijk twee hoeken in de cirkel: eentje kleiner dan $\pi$ en eentje groter dan $\pi$. Zo bepaalt de koorde $KA$ in ons plaatje niet alleen de hoek $\angle AmK$ in de driehoek $AmK$ maar ook de grote hoek die je krijgt als je met de klok mee langs de cirkel van $K$ naar $A$ loopt.

De formulering van de ongelijkheid door Aristarchus en het bewijs laat duidelijk zien dat hij telkens aan de kleinste van de twee bogen/hoeken dacht, en daar hoort de hoek bij die kleiner is dan twee rechte hoeken.

Opgave 3 Wat kun je zeggen over de tweede ongelijkheid van Aristarchus als je consequent de grootste van de twee bogen neemt? Ga op onderzoek uit.