De opkomst van data en AI gaat ook aan de sportwereld niet voorbij. Het bedrijf Beyond Sports gebruikt wiskundige methodes om sportwedstrijden op nieuwe manieren te visualiseren. In het voetbal beschikt het bedrijf onder andere over sensordata van spelers en de bal. Zo kunnen ze de wedstrijd real time simuleren in de stijl van Toy Story. Ook kunnen ze tijdens een wedstrijd het beeld laten veranderen van perspectief. Die succesvolle vrije trap kun je dan niet alleen zien vanuit de hoek van de camera op het veld, maar ook door de ogen van de keeper.

Het kortstepad-probleem

Heijerman ging aan de slag met een andere sport: American football. Een speler kan in deze sport op meerdere manieren scoren. Een manier is via een touchdown. Daarvoor brengt een speler de bal in de end zone, het gebied achter de doellijn, van de tegenstander. Maar hoe kan hij het beste lopen, afhankelijk van de positie en snelheid van de tegenstanders en zijn eigen teamleden? Dit wilde Beyond Sports weten, zodat sportanalisten die informatie kunnen gebruiken als ze een wedstrijd van commentaar voorzien.

Steijn Heijerman benaderde deze opdracht met twee elementen uit de wiskunde. Het kortstepad-probleem en het concept van de zogenoemde player influence.

Bij het kortstepad-probleem zoek je het kortste pad tussen een beginpunt en een eindpunt. Tussen deze twee punten liggen verschillende knooppunten. De afstanden tussen de knooppunten zijn bekend, en er zijn meerdere routes mogelijk. Het kan gaan om een fysieke afstand, in meters, maar bijvoorbeeld ook om de laagste kosten om goederen te vervoeren, of in de kortste tijd. In figuur 1 is een voorbeeld te zien. De kortste afstand tussen beginpunt $A$ en eindpunt $G$ gaat via $C, E, B$ en $D$.

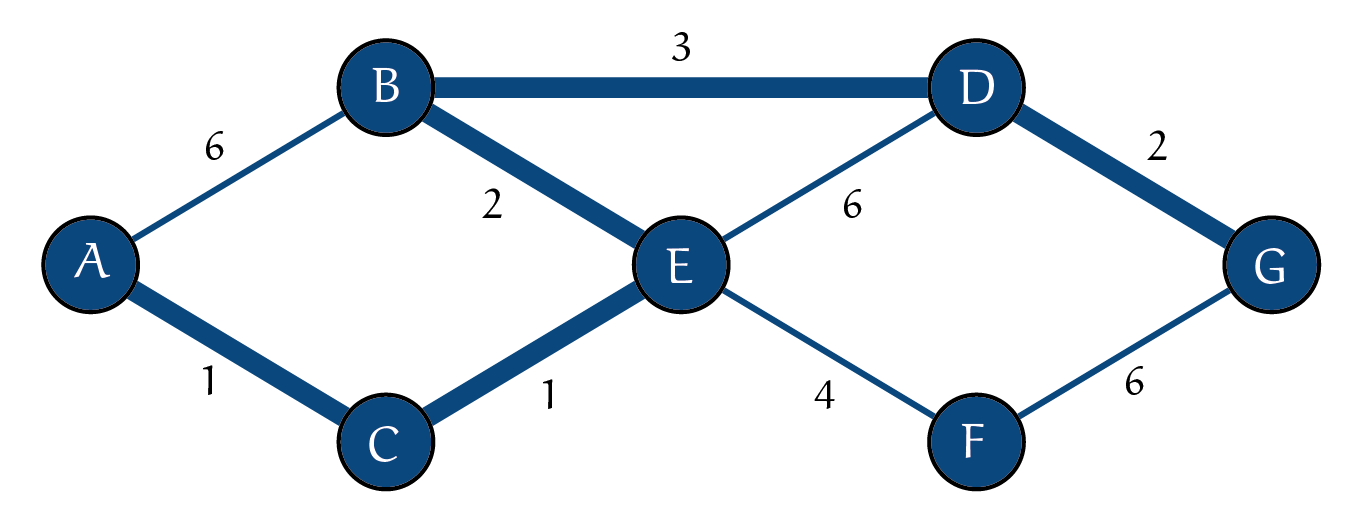
In dit voorbeeld kun je zelf nog wel achter de kortste route komen. Maar als het aantal knooppunten toeneemt is een andere aanpak nodig. Het algoritme van Dijkstra is een veelgebruikte methode om zo’n probleem op te lossen. Het geeft een stap-voor-stap instructie hoe je de kortste route vindt. En die taak kan een computer uitstekend op zich nemen. Google Maps gebruikt soortgelijke algoritmes om te bepalen hoe je het snelst op je gewenste bestemming komt. Wil je weten hoe dat algoritme werkt? Op pyth.eu vind je een link.

VeldControle

Het tweede element dat hij gebruikte is een wiskundige manier om de invloed van een speler op het voetbalveld te bepalen. Die player influence houdt rekening met de positie van een speler, de looprichting, zijn snelheid, en de positie van de bal. Bijvoorbeeld: hoe dichter een speler bij de bal is, of hoe meer hij in de richting van de bal beweegt, des te hoger zijn score. Voor elk punt op het veld kun je zo de veldcontrole van een team berekenen door de invloed van de tegenstanders af te trekken van de invloed van de eigen spelers. Deze maat vertaalde hij voor zijn onderzoek naar het American football. Wil een speler de end zone bereiken, dan moet hij plekken vermijden waar de tegenstander veel invloed heeft.

Oplossing: Een Creatieve aanpassing van afstanden

Schematische weergave van het American football veld, met raster en knooppunten. Het rode en blauwe gebied zijn de end zones van de twee teams.

Deze twee elementen leiden tot een optimale route. Eerst legde hij een raster van 1 bij 1 meter met knooppunten over het American footballveld (zie figuur 2). Vervolgens paste hij de afstand tussen de knooppunten aan, afhankelijk van de veldcontrole. Op plekken waar de tegenstander veel invloed had, vergrootte hij de afstand en hij verkleinde de afstand op de plekken met weinig invloed. De optimale route naar de end zone is de route met de kortste aangepaste afstand. En die kon hij met behulp van het algoritme van Dijkstra berekenen.

Resultaat: realistisChe routes

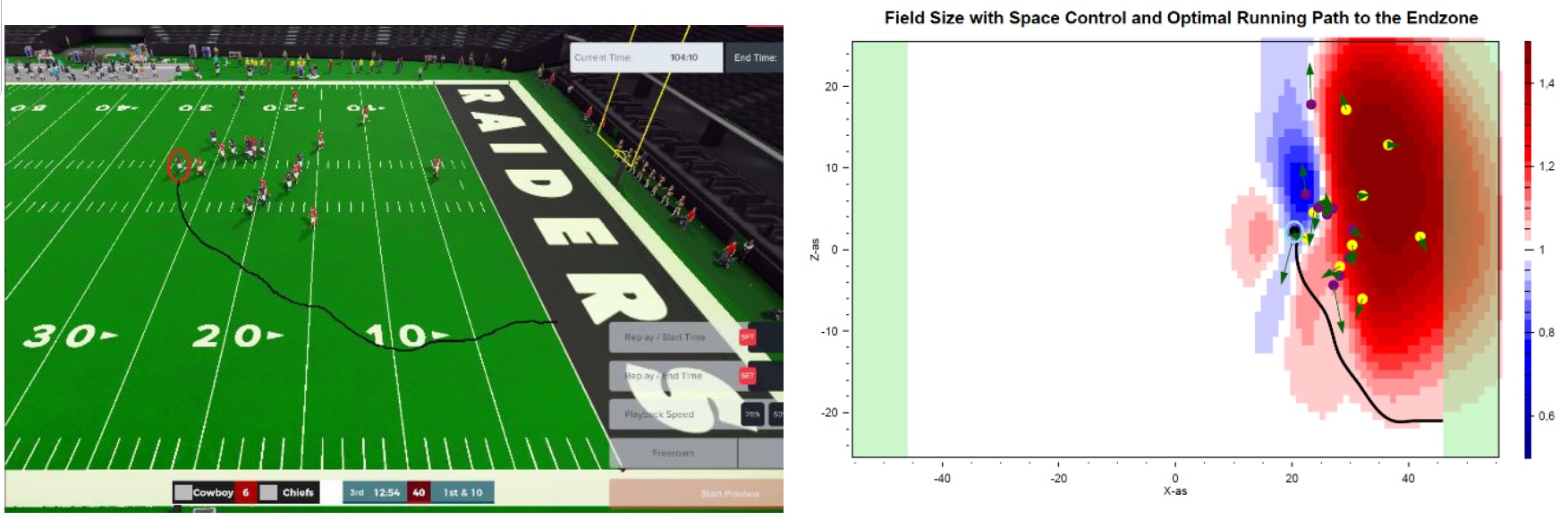
Werkt dit ook in de praktijk? Om dat te bepalen vergeleek hij de werkelijk gelopen paden met de optimale berekende routes. Een voorbeeld: in figuur 3 staat links de daadwerkelijk afgelegde route, rechts de berekende route. De zwarte stip geeft de locatie van de speler met de bal aan. De paarse puntjes zijn medespelers, de gele puntjes de tegenstanders. De pijlen geven aan welke kant iemand op beweegt. In het blauwe gebied heeft het aanvallende team controle. Hoe roder de kleur, hoe hoger juist de invloed van de tegenstander. Het donkerrode gebied moet een speler dus vermijden. De zwarte lijn geeft het berekende optimale pad aan. De speler neemt een omweg om de tegenstander te vermijden, en de route is erg vergelijkbaar met de daadwerkelijk gelopen route. Een prachtig resultaat. De methode geeft realistische uitkomsten en Beyond Sports kan deze gebruiken om de toeschouwer van inzichten te voorzien.

Voorbeeld van een kortstepad-probleem

		Edsger Dijkstra (1930-2002) wordt beschouwd als een van de meest invloedrijke onderzoekers binnen de wiskunde en de informatica. Hij was één van de eerste Nederlandse programmeurs en een grondlegger van de wiskundige fundamenten van de informatica. Dijkstra was van 1952 tot 1962 werkzaam op het Mathematisch Instituut, het huidige CWI (Centrum voor Wiskunde en Informatica). In 1959 ontwikkelde hij het kortstepad-algoritme, dat de kortste verbinding vindt tussen twee knooppunten in een graaf. Met dit algoritme vergelijk je niet alle mogelijke routes met elkaar, maar je onderzoekt per knooppunt de kortst mogelijke afstand tot het startpunt op een systematische manier. Je werkt daarbij met huidige, bezochte en niet-bezochte knooppunten. Het startpunt is het eerste huidige knooppunt, van daaruit kijk je naar de knooppunten die één stap vanaf het startpunt te bereiken zijn en noteer je de kortste afstand tot dit startpunt. Het startpunt wordt nu een bezocht knooppunt en het knooppunt met de kortste afstand tot het startpunt wordt het huidige punt. Op deze manier ga je steeds verder totdat je het eindpunt bereikt hebt. Dit algoritme wordt o.a. toegepast bij navigatiesystemen. In 1972 ontving Dijkstra de Turing Award, een onderscheiding die wel als de Nobelprijs voor de informatica wordt gezien. Meer informatie over Edsger Dijkstra vind je in Edsger W. Dijkstra: Brilliant, colourful, and opinionated.

 

		Miriam Loois en Linda Schouten zijn beide docent Toegepaste Wiskunde aan de Hogeschool van Amsterdam. Bij de opleiding Toegepaste Wiskunde leer je op een wiskundige manier naar vraagstukken te kijken. De wiskundige kennis en vaardigheden die je op de middelbare school hebt geleerd, worden flink uitgebreid. Verder leer je hoe je het aangeleerde kunt toepassen in verschillende domeinen zoals de logistiek en techniek. Afhankelijk van de Hogeschool waar je de opleiding volgt is er naast wiskundevakken als calculus en lineaire algebra aandacht voor statistiek, kansberekening, operations research, data science en artificial intelligence. Gedurende de hele opleiding werk je naast de theorievakken aan projecten waarin je het geleerde direct in de praktijk brengt en word je getraind in professionele vaardigheden als presenteren en projectmatig werken. Van de vier jaar die de opleiding duurt loop je ongeveer een jaar stage buiten school. Je kunt de opleiding op vijf HBO's volgen: bij Fontys in Eindhoven, de Haagse Hogeschool in Delft, bij de Hogeschool van Amsterdam en InHolland in Amsterdam en bij NHL Stenden in Leeuwarden.

 

De figuren zijn afkomstig uit de scriptei van Steijn. De hele scriptie kun je hieronder bij [Documenten] vinden.