In het voortgezet onderwijs in Griekenland is euclidische meetkunde een verplicht vak in het curriculum. Ik ben in Griekenland opgegroeid, dus ook daar naar school gegaan. In de vierde klas kregen we een dik boek met als titel "Meetkunde", en op de eerste pagina stonden de vijf postulaten van Euclides. Twee jaar lang waren we bezig met lijnen, driehoeken, cirkels, oppervlakken, en heel veel stellingen! Ik vond meetkunde een heel leuk vak, want ik kon alles tekenen. Toen twee jaar later het vak afgerond was, dacht ik dat we alles in de meetkunde hadden behandeld. Wat een misvatting! Tijdens mijn bachelor-opleiding kwam ik een resultaat van Euler tegen dat ik  nooit eerder had gezien. Dit resultaat had een ander karakter dan alle resultaten die ik op school had gezien. Deze stelling zei iets over de aard van veelvlakken, het was een formule die de bouwstenen van een veelvlak, namelijk de hoekpunten, de ribben en de zijvlakken, met elkaar verbond.

Convexe veelvlakken

We beschouwen een convex veelvlak. Een veelvlak is een meetkundig object in drie dimensies dat samengesteld is uit een eindig aantal veelhoeken. Voorbeelden van veelvlakken zijn de kubus, het viervlak, de vierzijdige piramide, enzovoort.

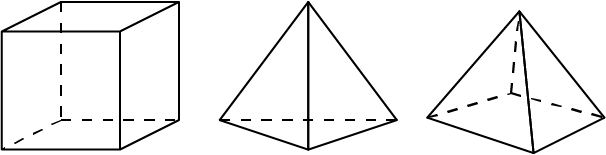
Een kubus, een viervlak en een vierzijdige piramide

We noemen een veelvlak convex als het aan de volgende eis voldoet.

Neem twee willekeurige punten die op een veelvlak liggen en teken het lijnstuk dat deze twee punten verbindt. Is het een convex veelvlak, dan ligt dit lijnstuk altijd geheel in het inwendige van het veelvlak.

De drie veelvlakken hierboven zijn allemaal convex. Een voorbeeld van een niet-convex veelvlak is de tetrahemihexahedron.

Een tetrahemihexahedron

Om te begrijpen waarom de tetrahemihexahedron niet convex is moeten we naar de groene vlakken gaan kijken in figuur 2. De groene vlakken zijn samengesteld uit drie driehoeken die samen een piramide vormen met een punt naar het inwendige van het veelvlak. We zien dus dat de lijn die het hoekpunt $A$ en punt $B$ verbindt niet in het inwendige van het veelvlak ligt, dus de tetrahemihexahedron is niet convex. 

De bouwstenen van een veelvlak

Een veelvlak is gekenmerkt door drie bouwstenen, het aantal hoekpunten ($V$, van vertices), het aantal ribben ($E$, van edges) en het aantal zijvlakken ($F$, van faces). Voor elk veelvlak, convex of niet convex, zijn deze drie getallen goed gedefinieerd. Voor de voorbeelden boven worden deze karakteristieken gegeven in de volgende tabel.

		$V$		$E$		$F$
Kubus		$8$		$12$		$6$
Viervlak		$4$		$6$		$4$
Vierzijdige piramide		$5$		$8$		$5$
Tetrahemihexahedron		$6$		$12$		$7$

In mijn ogen is het niet vanzelfsprekend dat er een verband bestaat tussen deze drie bouwstenen van een veelvlak. In de achttiende eeuw heeft de wiskundige Leonard Euler de volgende formule ontdekt die een verband legt tussen $V$, $E$ en $F$ in een convex veelvlak. 

Eulers formule voor veelvlakken

$$V-E+F=2.$$

$(1)$

Wat zo magisch is, is dat deze formule geldt in alle convexe veelvlakken! Neem bijvoorbeeld de kubus, dan is volgens de bovenstaande tabel $V - E + F = 8 - 12 + 6 = 2$.

Voor het viervlak en de piramide komt het ook precies op $2$ uit. Ga ook zelf aan de slag, neem een ander convex veelvlak en verifieer dat $V - E + F = 2$. Let op, je veelvlak moet convex zijn, er mogen geen gaten in zitten en ook geen stekels uitsteken! In de tetrahemihexahedron zien we bijvoorbeeld dat $V - E + F$ gelijk is aan $1$.

Opgave 1

Verifieer deze berekening voor de tetrahemihexahedron. (Op Wikipedia kun je een roterend model vinden.)

En nu de essentie van dit artikel. We hebben deze formule verifieerd voor drie gevallen van convexe veelvlakken, maar hoe kunnen we laten zien dat die geldt in alle convexe veelvlakken? Is het misschien mogelijk om een ingewikkeld veelvlak te construeren dat convex is en tegelijkertijd niet aan deze formule voldoet? Laten we even kijken waarom dat niet mogelijk is.

Het bewijs dat we gaan bespreken, bedacht door de wiskundige Augustin-Louis Cauchy in 1811, maakt gebruik van Schlegeldiagrammen. Dit zijn graaf-representaties van een convex veelvlak op het platte vlak. Het bewijs legt een verband tussen twee grote onderdelen van de wiskunde, het meer klassieke onderdeel van de meetkunde, en het meer moderne onderdeel van de grafentheorie. Een graaf is een diagram waarin punten (ook wel knopen genoemd) met elkaar verbonden zijn door lijnen (meestal zijden of kanten genoemd). Het idee is dat als we een veelvlak gaan projecteren op het platte vlak we een graaf krijgen, die het Schlegeldiagram van het veelvlak wordt genoemd. Laten we kijken hoe dit werkt met een paar voorbeelden.

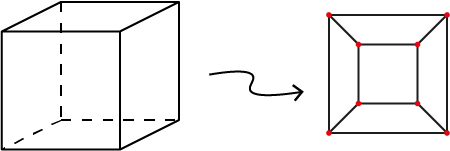
De projectie van de kubus op het vlak

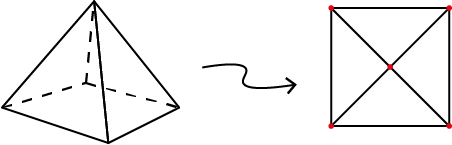
De projectie van de vierzijdige piramide op het vlak

Opgave 2

Maak het Schlegeldiagram van het viervlak.

Deze graaf heeft twee belangrijke eigenschappen. Ten eerste hij heeft hetzelfde aantal punten en zijden als het oorspronkelijke veelvlak en heeft één zijvlak minder. De tweede eigenschap is dat hij planair is, dat betekent dat geen twee zijden elkaar snijden. Dus om Eulers formule te bewijzen voor een convex veelvlak is het voldoende om te bewijzen dat in een planaire graaf de volgende formule geldt

$$V-E+F=1.$$

$(2)$

We hebben dus een meetkundig probleem vertaald naar een probleem in de grafentheorie! Dat is zo mooi met de wiskunde, dat je soms naar een andere wereld mag reizen om iets te bewijzen! We gaan dus verder met het bewijs voor planaire grafen. 

We beschouwen een planaire graaf. Het idee is dat we deze graaf gaan transformeren, door middel van operaties op de zijvlakken, naar een eenvoudiger graaf op zo’n manier dat het linkerlid van $(2)$ hetzelfde blijft. De twee operaties die we gaan toepassen op de graaf zijn als volgt.

Operatie 1

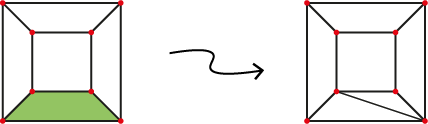
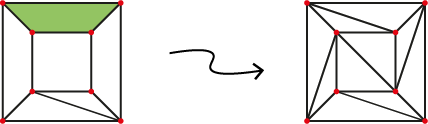
Zoek in de graaf een zijvlak met meer dan drie punten. We verbinden twee van deze punten. Dan krijgen we een nieuwe ribbe in de graaf en twee zijvlakken in plaats van één. Dus in de nieuwe graaf $V_2 = V$, $E_2 = E + 1$ en $F_2 = F + 1$, en $V_2 - E_2 + F_2 = 1$. Dus $V - E + F$ blijft hetzelfde en bovendien is de graaf nog steeds planair. We herhalen deze procedure totdat het niet meer kan. Op het einde krijgen we een graaf die is opgebouwd uit veel driehoeken, misschien met gekromde zijden maar dit maakt niet uit voor het bewijs.

(Links) Het zijvlak in groen heeft vier punten. (Rechts) We verbinden de twee punten (de andere twee hadden ook gekund), we krijgen één zijvlak en één ribbe extra.

(Links) We herhalen de operatie, het zijvlak in groen vier punten. (Rechts) Op het einde krijgen we een graaf die is opgebouwd door veel driehoeken.

Operatie 2

De tweede operatie heeft als doel om zijvlakken te verwijderen onder de voorwaarde dat $V - E + F$ gelijk blijft. In onze graaf kan elk zijvlak $0, 1, 2$ of $3$ gemeenschappelijke ribben hebben met het buitenvlak van de graaf. We verwijderen een ribbe van een zijvlak die één gemeenschappelijke ribbe heeft met het buitenvlak. Dan verdwijnen één ribbe en één zijvlak en dus houdt de formule dezelfde uitkomst. We herhalen deze procedure totdat het niet meer kan.

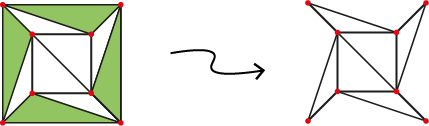
(Links) Met groen de zijvlakken die één gemeenschappelijke ribbe hebben met het buitenvlak. (Rechts) Deze zijvlakken mogen we verwijderen.

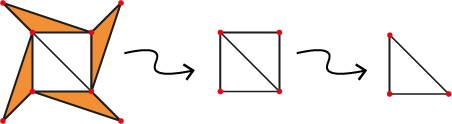
(Links) Met groen de zijvlakken die één gemeenschappelijke ribbe hebben met het buitenvlak en met oranje de zijvlakken die twee hebben. (Rechts) De graaf nadat we alle ribben hebben verwijderd van zijvlakken die één gemeenschappelijke ribbe hebben met het buitenvlak.

Opgave 3

Laat zien dat deze operatie $V-E+F$ gelijk laat.

Vervolgens gaan we zijvlakken verwijderen die twee gezamenlijke ribben hebben met het buitenvlak. Ook dan blijft $V-E+F$ onveranderd (ga dit na!). Uiteindelijk hebben we een graaf die een driehoek is en voor driehoeken weten we dat de formule geldt!
Quod erat demonstrandum!

Opgave 4

Laat zien dat in een driehoek $V-E+F=1$.

We hebben dus bewezen dat in elk convex veelvlak geldt dat $V - E + F = 2$. We hebben ook een voorbeeld van een niet-convex veelvlak, namelijk de tetrahemihexahedron, waarvoor deze formule niet geldt. Dus de formule geldt niet voor alle veelvlakken. Maar is convexiteit ook noodzakelijk? Zijn er niet-convexe veelvlakken waarvoor de desbetreffende formule wel geldt? Het antwoord is: ja! Neem bijvoorbeeld een kubus met een piramide erboven op, waarvan het grondvlak kleiner is dan een zijde van de kubus!

Opgave 5

Maak een plaatje van een kubus met een kleinere piramide erboven op en laat zien dat $V - E + F = 2$.

Kunnen we dit verklaren? In het bewijs we hebben we eigenlijk een sterker resultaat bewezen, namelijk dat in elke planaire graaf geldt dat $V - E + F = 1$. Laten we het Schlegeldiagram van dit veelvlak gaan tekenen, het is een planaire graaf!

Opgave 6

Teken het Schlegeldiagram van een kubus met een kleinere piramide erbovenop.

De platonisChe liChamen

Een platonisch lichaam, of anders een regelmatig veelvlak, is een veelvlak waarvan de zijvlakken identieke regelmatige veelhoeken zijn en op elk hoekpunt hetzelfde aantal zijvlakken samenkomen. Een voorbeeld van een regelmatig veelvlak is de kubus, elk zijvlak is een vierkant. Veel interessante vragen komen nu boven. Welke andere regelmatige veelvlakken bestaan er? En hoeveel zijn er? Kan ik met elke regelmatige veelhoek een regelmatig veelvlak maken? Laten we deze vraag gaan onderzoeken! Ten eerste realiseren we ons dat met elk veelvlak er een uniek drietal getallen $(V,E,F)$ correspondeert, vanwege de formule van Euler in $(1)$. Maar gegeven een $(V,E,F)$ is het niet zo makkelijk te zien wat voor veelvlak het representeert. Kun jij bijvoorbeeld zien welk veelvlak $(8,12,6)$ voorstelt? Het is de kubus maar het is in eerste instantie niet zo makkelijk te zien. Het is interessanter om te weten hoeveel zijvlakken samenkomen in elk hoekpunt, dat noteren we met $H$, en hoeveel ribben elk zijvlak heeft, dat noteren we met $R$. Voor de kubus is bijvoorbeeld $H=3$ en $R=4$, dus drie vierkanten komen samen in elk punt. Beschouw een regelmatig veelvlak en kijk naar alle zijvlakken los van elkaar. Dan krijg je $F$ veelhoeken met totaal $2\cdot E$ ribben en $H\cdot V$ punten. Dit leidt tot de vergelijking $H\cdot V = R\cdot F$. Laten we eerst kijken waarom deze vergelijking geldt: We hebben $F$ veelhoeken (de zijvlakken) met totaal $H\cdot V$ punten. Het aantal ribben in elk veelhoek, genoemd $R$, is gelijk aan het aantal hoekpunten van die veelhoek, en het aantal hoekpunten in elke veelhoek is gelijk aan $\frac{VH}{F}$, dus $R = \frac{VH}{F}$ of $R\cdot F = V\cdot H$.

Opgave 7

Bewijs met een vergelijkbare redenering dat $R\cdot F = 2\cdot E$.

Opgave 8

Verifieer deze twee vergelijkingen voor de kubus, het viervlak en de vierzijdige piramide.

Als we deze twee vergelijkingen gaan combineren met Euler’s formule dan krijgen we de vergelijking

$$\frac{1}{H} + \frac{1}{R} - \frac12 = \frac{1}{E}$$

en dus moeten $H$ en $R$ voldoen aan de ongelijkheid

$$\frac{1}{H} + \frac{1}{R} - \frac12 > 0.$$

Tegelijkertijd moet $H$ ook groter zijn dan of gelijk aan $3$, om een driedimensionaal veelvlak te hebben. Naarmate $H$ en $R$ groeien, wordt $\frac{1}{H} + \frac{1}{R}$ kleiner, dus we verwachten dat voor $H$ en $R$ groot genoeg $\frac{1}{H}+\frac{1}{R} - \frac12$ negatief wordt. Dus de vraag is, hoe groot moeten $H$ en $R$ zijn? De resultaten zijn in de volgende tabel gegeven.

$R$		$H<\frac{2\cdot R}{R-2}$		$H$
$3$		$H<6$		$3,4,5$
$4$		$H<4$		$3$
$5$		$H<\frac{10}{3}$		$3$
$6$		$H<3$		-

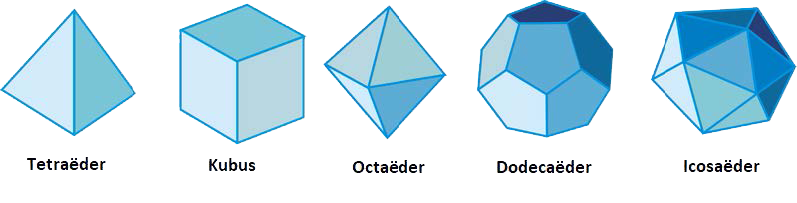
De conclusie is dat er precies vijf regelmatige veelvlakken bestaan, ook de vijf platonische lichamen genoemd. Dit zijn de tetraëder $(H=3, R=3)$, de kubus $(H=3, R=4)$, de octaëder $(H=4, R=3)$, de dodecaëder $(H=3, R=5)$ en de icosaëder $(H=5, R=3)$.

Een voetbal

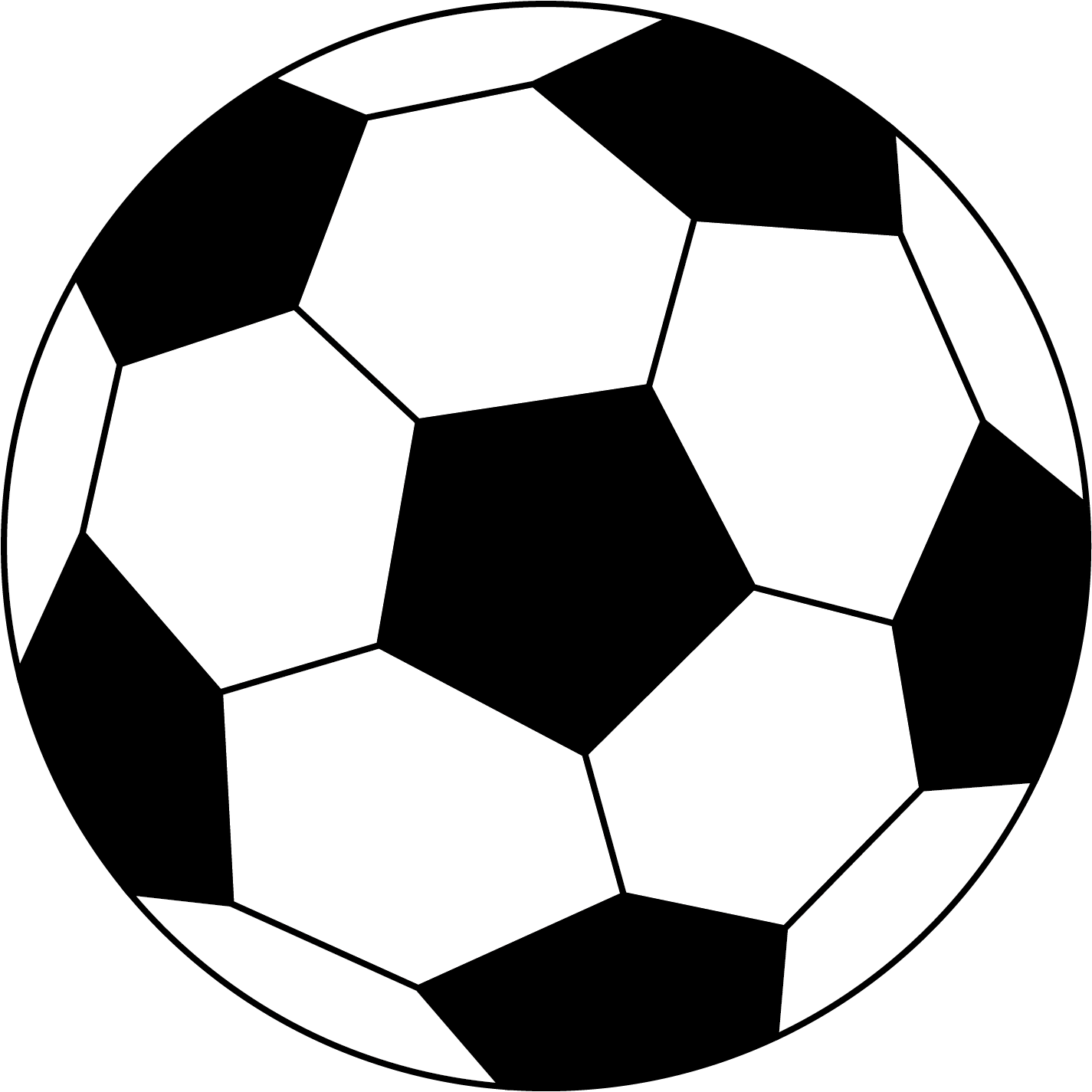
Heb je ooit een voetbal goed bekeken? Een voetbal is niet echt helemaal rond. Het oppervlak van een voetbal is eigenlijk samengesteld uit twee soorten veelhoeken, namelijk vijfhoeken en zeshoeken. Die hebben allemaal ook een beetje kromming natuurlijk zodat de voetbal makkelijk kan rollen. Stel dat er $v$ vijfhoeken zijn en $z$ zeshoeken. Dan levert Euler’s formule de vergelijking 

$$\frac{5v+6z}{3} - \frac{5v+6z}{2} + v+z=2.$$

$(3)$

Opgave 9

Laat zien dat in een voetbal $V=\frac{5v+6z}{3}$, $E=\frac{5v+6z}{2}$ en $F=v+z$. Los de vergelijking in $(3)$ op. Hoeveel vijfhoeken heeft een voetbal? En hoeveel zeshoeken?

 

	Jaargang 42 (2002-2003) van Pythagoras stond in het teken van veelvlakken. Ook Eulers formule is toen uitgebreid aan bod gekomen. De jaargang is te vinden in het archief op pyth.eu. Zo vind je in Pytagoras 42-1 (oktober 2002) onder andere het artikel "De regelmaat van veelvlakken".

 

	Over de Network Pages In dit artikel heb ik een resultaat uit de meetkunde gepresenteerd. Dit resultaat heb ik bewezen door middel van grafen. Grafentheorie is een bloeiende discipline binnen de wiskunde en heel belangrijk voor de theorie van netwerken. De Network Pages is een online platform waar we allerlei mooie resultaten uit de netwerktheorie bespreken. Je kunt ook verder lezen over Eulers formule. Maar we hebben veel meer! www.networkpages.nl/understanding-geometry-using-graphs/ www.networkpages.nl/category/basisbegrippen/ www.nemokennislink.nl/publicaties/ken-uw-lichamen/

 

Bekijk oplossing