Stel dat bekend is – bijvoorbeeld op grond van de historie − dat bij de productie van een bepaald soort lampje er een vaste kans is dat zo’n lampje een defect vertoont, bijvoorbeeld 0,1% voor elk lampje. Als we een steekproef van 2000 lampjes nemen, hoe groot is dan de kans op precies 3 lampjes met een defect? Dit probleem kun je oplossen met de binomiale verdeling. We gaan er in dit artikel vanuit dat je met deze kansverdeling bekend bent. Als $X$ het aantal defecte lampjes in de steekproef is, dan is $X$ binomiaal verdeeld met parameters $n = 2000$ en $p = 0,001$. Voor de gevraagde kans $\textbf{P}(X = 3)$ geldt het volgende:
$$ \textbf{P}(X=3) = {2000\choose 3} \cdot 0,001^3 \cdot 0,999^{1997} \approx 0,1805.$$

De letter P komt van het Latijnse woord probabilitas of het Engelse probability. De factor ${2000 \choose 3}$ is het aantal combinaties van 3 uit 2000. Grafische rekenmachines bieden de mogelijkheid om binomiale kansen snel uit te rekenen. Bij de TI-84+ voer je in: binompdf(2000,0.001,3). Rekenmachines van andere merken hebben soortgelijke opties. Ook kun je Excel of WolframAlpha gebruiken.

Poissonverdeling

Je kunt de kans op 3 defecte lampjes echter ook berekenen met de ‘Poissonformule’:
$$\textbf{P}(X = 3) = \frac{\lambda^3}{3!} \cdot e^{-\lambda}. $$

Hierbij staat $\lambda$ (de Griekse kleine letter ‘lambda’) voor het gemiddelde (of verwachte) aantal defecte lampjes in de steekpoef, dus $n · p = 2000 \cdot 0,001 = 2$. Verder is $e$ het grondtal van de natuurlijke logaritme, een getal dat in allerlei wiskundige en andere formules opduikt. We krijgen dus:
$$\textbf{P}(X = 3) = \frac{2^3}{3!} \cdot e^{–2} \approx 0,1804,$$ een antwoord dat nauwelijks verschilt van de binomiale kans.

Opdracht 1. Bereken de kans op precies 4 branden in een willekeurige week in een stad, als het gemiddelde aantal branden in die stad per week 7 is. Bereken ook de kans op 0, 6 en 7 branden in een willekeurige week.

De naamgever van deze kansverdeling, Siméon Denis Poisson (1781-1840) was een leerling van Pierre-Simon Laplace (1749-1827), die de eerste definitie van het begrip kans voorstelde. Poisson was hoogleraar mechanica in Parijs. Hij had enige tijd de leiding over het wiskundeprogramma van het Franse middelbaar onderwijs. Poisson introduceerde ‘zijn’ kansverdeling over relatief zeldzame gebeurtenissen in 1837. Net als binomiale kansen kun je ook Poissonkansen met een grafische rekenmachine berekenen. Met de TI-84+ is het poissonpdf(2,3).

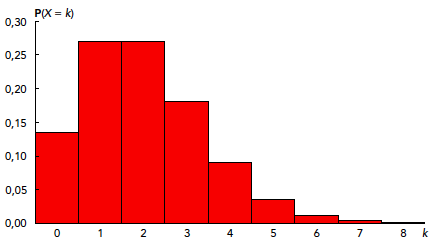
Figuur 1 Kanshistogram van de Poissonverdeling voor λ = 2, voor $k$ = 0, 1 , 2, …, 8

Opdracht 2. Bereken de kans op precies 18 schietincidenten in één jaar bij de Nederlandse politie als gegeven is dat het gemiddelde aantal schietincidenten per jaar 13,5 is (politiegegevens uit 2013 en de vijf jaar ervóór).

Opdracht 3. Laat zien dat als $\lambda$ een geheel getal is, er altijd twee gelijke kansen in de bijbehorende Poissonverdeling optreden.

De Poissonkans van het voorbeeld (de kans op 3 defecte lampjes in een steekproef van 2000) is een zeer goede benadering van de binomiale kans: pas in de vierde decimaal zit verschil. Dit geldt ook voor andere aantallen defecte lampjes. Wanneer kun je een binomiale kansverdeling goed door een Poissonverdeling benaderen? Daarvoor gelden de volgende vuistregels:

• $n \geq 20$;
• $np < 5$ of $n(1 − p) < 5$.

In ons lampjesvoorbeeld is aan beide eisen voldaan, want $n = 2000$ en $np = 2$ en dus kleiner dan 5. Ter illustratie zetten we de kansen voor de aantallen 0 tot en met 6 in een tabel (zie tabel 1). Het kanshistogram van de Poissonverdeling met $\lambda = 2$ (maar bij goede benadering dus ook die van de binomiale verdeling met $n = 2000$ en $p = 0,001$) zie je in figuur 1.

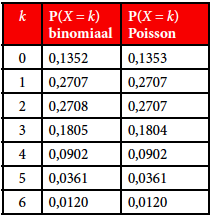
Tabel 1

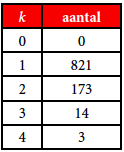
Tabel 2

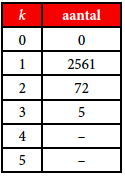
Tabel 3

Tabel 4

Een verschil tussen de twee kansverdelingen is dat bij de binomiale verdeling alleen de uitkomsten 0 tot en met $n$, de steekproefgrootte, mogelijk zijn, terwijl er voor de Poissonverdeling geen bovengrens is. Een belangrijker verschil is dat de Poissonverdeling maar één parameter ($\lambda$, het gemiddelde) heeft. De binomiale verdeling heeft er twee ($n$ en $p$). In de praktijk is de Poissonverdeling zo gemakkelijk toe te passen, omdat $\lambda$ vaak gemakkelijk te meten is. Neem bijvoorbeeld de branden uit opdracht 1: de waarde $\lambda = 7$ is gemakkelijk te bepalen. Dat in zo’n geval ook aan de twee eisen van de vuistregel wordt voldaan, mag je wel aannemen: er zijn heel veel plekken in de stad waar brand kan ontstaan ($n$ is dus al gauw veel groter dan 20) en de kans op een brand is maar heel klein (waardoor $np$ kleiner dan 5 is).

Vaak gaat het bij toepassingen van de Poissonverdeling om zogeheten ‘wachttijdproblemen’, bijvoorbeeld het aantal klanten dat per dag een bepaalde winkel bezoekt, het aantal schepen dat per uur een haven binnenkomt, het aantal patiënten bij de eerstehulpafdeling per dag. Maar de verdeling kan tevens gebruikt worden voor het aantal fouten in een jaarrekening, het aantal storingen in een machinepark van een fabriek per dag of, zoals we straks als speciaal voorbeeld zullen geven, het aantal keren dat een fietsendief wordt opgepakt. Al deze ‘telproblemen’ blijken goed beschreven te kunnen worden door de Poissonverdeling.

Fietsendieven

Een mooie toepassing van de Poissonverdeling is die bij een schatting van wat in de literatuur bekend staat als size of the criminal population. Een Nederlandse variant hiervan dook een aantal jaren geleden op. De casusbeschrijving is als volgt.
In Amsterdam is men geïnteresseerd in de omvang van de ‘groep’ fietsendieven, inclusief de fietsendieven die nog nooit gepakt zijn. Men vermoedt dat deze laatste groep vrij groot is. Maar hoe schat je de grootte van een groep personen die je nog nooit hebt ingerekend?
Stel dat de volgende gegevens bekend zijn. Het aantal fietsendieven dat één keer is opgepakt, is 821. Verder zijn er 173 fietsendieven twee keer gevat, 14 personen zijn drie keer gearresteerd voor fietsendiefstal, en 3 personen vier keer. We nemen aan dat het aantal keren $X$ dat een fietsendief wordt opgepakt bij benadering Poissonverdeeld is. We zoeken nu de ‘best passende’ Poissonverdeling bij de gegeven aantallen.
De gegeven aantallen personen die $k$ keer betrapt zijn, zijn weergegeven in tabel 2. Merk op dat we het gemiddelde aantal voor $k$ hier niet kennen, omdat het aantal niet-betrapte fietsendieven (uiteraard) niet bekend is.
Het doel is een schatting te geven van het aantal fietsendieven dat nog niet betrapt is (!) en daarmee dus van de size of the criminal population, dus de grootte van de groep van alle fietsendieven, ook de (nog) niet betrapte. Dit gaan we doen door de Poissonverdeling alleen te bekijken voor $k = 1, 2, ...$, dus zonder $k = 0$. Deze nieuwe kansverdeling heet de ‘zero-truncated’ Poissonverdeling, in het Nederlands vertaald door ‘nul-afgekapte’ Poissonverdeling. Volgens de Poissonformule geldt voor de kans dat een fietsendief 0 keer is betrapt het volgende:

$$\textbf{P}(X=0) = \frac{\lambda^0}{0!} e^{-\lambda} = e^{-\lambda}.$$
Volgens de complementregel is de kans dat een fietsendief minstens één keer is betrapt gelijk aan
$$\textbf{P}(X\geq 1 ) = 1-e^{-\lambda}.                                                                                    (\star)$$
Als we nu uit een Poissonverdeling de waarde $k = 0$ weglaten en alle kansen voor $k = 1, 2, 3,…$ opnieuw berekenen, dan zijn de kansen bij de 0-afgekapte Poissonverdeling gelijk aan

$$\textbf{P}(X=k|X\geq 1) = \frac{\lambda^k e^{-\lambda}}{k!(1-e^{-\lambda}},$$

namelijk de oorspronkelijke Poissonkansen gedeeld door de waarde in (*). Dit is een voorwaardelijke kans; achter de verticale streep staat de ‘voorwaarde’. De kans dat $X = 1$ in deze 0-afgekapte Poissonverdeling is gelijk aan
$$\textbf{P}(X =1|X \geq1)= \frac{\lambda e^{-\lambda}}{1-e^{-\lambda}} =  \frac{\lambda}{e^\lambda}-1.  (\star \star)$$ 

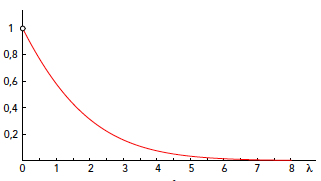
Figuur 2 De grafiek van $λ/(e^λ – 1)$ als functie van λ

Hoe je het meest rechtse lid verkrijgt? Vermenigvuldig teller en noemer van het middelste lid maar met $e^{\lambda}$, dan zie je het meteen.
De grafiek van deze kans, als functie van $\lambda$, is getekend in figuur 2. Merk op dat de functiewaarde voor $\lambda = 0$ niet gedefinieerd is, maar in de limiet nadert tot 1.

Met de praktijkgegevens kunnen we nu een goede schatting van $\lambda$ vinden. We weten immers dat het aantal fietsendieven dat één keer is betrapt, gelijk is aan 821. En de aantallen dieven die twee, drie en vier keer zijn opgepakt, zijn achtereenvolgens 173, 14 en 3 (zie tabel 2). Dat betekent dat een benadering van (**) wordt gegeven door
$$\frac{821}{821+173+14+3} = \frac{821}{1011} \approx 0,8121. $$
We zoeken dus de oplossing van de vergelijking
$$\frac{\lambda}{e^{\lambda}-1}  =0,8121.$$ Met een grafische rekenmachine, Excel of WolframAlpha vinden we $\lambda \approx 0,4029$. Met deze schatting voor $\lambda$ is het mogelijk om een schatting van de kans op het aantal niet-betrapte fietsendieven te berekenen:
$$e^{-\lambda} = e^{-0,4029} \approx 0,6684.$$
en schatting van het aantal niet-betrapte fietsendieven is dan
$$\frac{0,6684}{ 1−0,6684} ·1011\approx 2038.$$
De breuk met noemer $1 − 0,6684$ is nodig om de 0-truncated Poissonkans weer terug te voeren naar de oorspronkelijke Poissonverdeling. Het totale aantal fietsendieven − de size of the criminal population − is dan dus 2038 + 1011 = 3049.
Tot slot: om tot dit resultaat te komen, hebben we gebruikgemaakt van een schatting (op grond van de praktijkgegevens) voor $\textbf{P}(X = 1 | X \geq 1).$ We hadden ook de kans $\textbf{P}(X = 2 | X \geq 1)$, of voor waarden groter dan 2, erbij kunnen betrekken. Dat maakt het allemaal wat ingewikkelder – leuk voor eigen onderzoek!

 

Opdracht 4. Schat de size of the criminal population in het geval van het aantal aanhoudingen van personen die k keer betrapt zijn op het illegaal bezit van een vuurwapen. Gebruik daartoe tabel 3. Deze gegevens komen uit het artikel ‘Estimating the size of a criminal population from police records using the truncated Poisson regression model’ van P.G.M. van der Heijden et al, Statistica Neerlandica (2003), 57-3, p. 289-304.

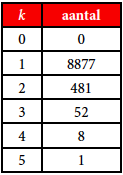
Opdracht 5. Schat de size of the criminal population in het geval van het aantal aanhoudingen van personen die $k$ keer betrapt zijn op rijden onder invloed. Gebruik tabel 4 (de bron is dezelfde als bij tabel 3).

 

Bekijk oplossing