De auteur bestudeert een mozaïektableau in Isfahan. Over het patroon van witte lijnen met achtpuntsterren liggen grotere geometrische vormen zoals vierpuntige sterren en vliegers. Deze zijn gedecoreerd met bloemmotieven of kufi-tekst (een hoekig Arabisch schrift dat alleen kenners kunnen ontcijferen).	Detail van een wanddecoratie op een binnenplaats bij een moskee in Isfahan. Een mooi voorbeeld van de combinatie van kalligrafie met meetkundige patronen.

De islamitische ornamentiek kenmerkt zich door een drietal unieke stijlelementen (zie figuur 1 en 2): heilige teksten in sierlijke kalligrafie of strak en hoekig ‘kufi’ schrift; gestileerde kleurrijke bloemmotieven, vaak gecombineerd met gebladerde takken in spiraalvorm; en –niet het minst belangrijk– de mozaïeken, gebaseerd op geometrische patronen. Die laatste hebben van de 7^e tot de 18^e eeuw een fascinerende ontwikkeling doorgemaakt in regio’s die zich uitstrekken van Marokko en zuidelijk Spanje via heel noordelijk Afrika, Turkije tot in Pakistan en India, elke regio met zijn eigen specialismen. Die ontwikkeling werd wellicht veroorzaakt doordat op heilige gebouwen geen mens- of dierfiguren mochten worden afgebeeld. Maar wat ook een rol speelde was het feit dat men in de genoemde regio’s al veel wist over meetkunde dankzij de hoogontwikkelde astronomie en de studie die Arabische en Perzische geleerden maakten van Griekse geschriften van wiskundigen als Pythagoras en Euclides.

Het kenmerkende aan de patronen is, dat er verschillende vormen van symmetrie in zitten: Spiegelsymmetrie, draaisymmetrie en schuifsymmetrie (ook wel translatiesymmetrie). Ook is het zo, dat de vormpjes zelf, waaruit elk mozaïek is opgebouwd, vrijwel altijd symmetrisch zijn en vaak een welbekende wiskundige vorm hebben, bijvoorbeeld die van een ruit, een vlieger of een regelmatige veelhoek. Verder is in bijna elk mozaïek wel een regelmatige stervorm te vinden. Vanwege de schuifsymmetrie (meestal zowel in horizontale als in verticale richting) zijn de mozaïeken oneindig uit te breiden in alle richtingen. In de ontwerpen die je op gebouwen en ook in heilige boeken ziet vallen de randen van de tableaus vaak samen met symmetrieassen van het patroon. Zie figuur 3.

Hier is te zien dat de randen van het tableau samenvallen met symmetrieassen van het patroon. Zo ontstaan bij de randen halve sterren.

Er zijn in een tijd van ongeveer duizend jaar vele honderden verschillende patronen ontworpen. Alle ontwerpen werden geconstrueerd met passer en liniaal, eventueel voor het gemak aangevuld met een ‘rechte hoek’, gemaakt van hout. De specialisten moeten goed onderlegd zijn geweest in de ontwerptechniek. Hoe ze te werk gingen is niet meer precies te achterhalen doordat de kennis veelal mondeling werd doorgegeven: er zijn maar weinig oude constructietekeningen bewaard gebleven en niemand heeft destijds nauwkeurig opgeschreven hoe de patronen stap voor stap getekend moesten worden, laat staan dat er beschreven is hoe men zo’n constructie precies bedacht had! Zeker is, dat de oorspronkelijke ontwerpers veel kennis hadden van constructietechnieken. Ze waren excellent in hun vak, een vak dat je zou kunnen zien als een vorm van toegepaste wiskunde: Geen wiskunde waarin je zoekt naar bewijzen van stellingen, maar een wiskunde waarin het uiteindelijke doel is om mooie patronen te ontwerpen.

In het huidige Iran ontwikkelden de Perzen ongeveer een millennium geleden een specifieke ontwerpwijze: de ‘tegen-elkaar-aanliggende-veelhoeken-methode’, kortweg ook wel ‘girih’ genoemd, naar het Perzische woord voor knoop, of snijpunt. Deze methode is misschien wel de meest belangwekkende en wijdverspreide tekentechniek, waarmee de Islamitische ornamentiek zich onmiskenbaar heeft weten te onderscheiden. Het mooie van deze techniek is, dat die breed toepasbaar is en een heel scala van mozaïeken weet te produceren, uiteenlopend van tamelijk eenvoudig tot enorm complex, terwijl het basisprincipe niet eens zo moeilijk is.

Vroeger moesten de ambachtslieden alles met enkel passer en liniaal doen. Tegenwoordig hebben we de beschikking over digitale tekenprogramma’s. Toch is het een leuke uitdaging om zonder computer aan de slag te gaan: Handgetekende mozaïeken zijn, juist door de imperfectie, vaak veel mooier dan tekeningen met de computer. Ook nu houden zich dan ook vele honderden, misschien wel duizenden mensen zich bezig met het tekenen van handgemaakte geometrische patronen. Om tijd te winnen, kun je echter wel gebruik maken van digitaal getekende werkbladen waarop je je eigen ontwerpen met de hand construeert. Deze kun je vervolgens overtrekken, inkleuren, versieren enzovoort.

In de rest van dit artikel kun je zien hoe de basis-ontwerptechniek werkt. Met wat oefening kun je vervolgens ook zelf mooie mozaïeken tekenen. In het vervolgartikel dat in een volgende nummer van Pythagoras uitkomt kijken we naar complexere ontwerpen.

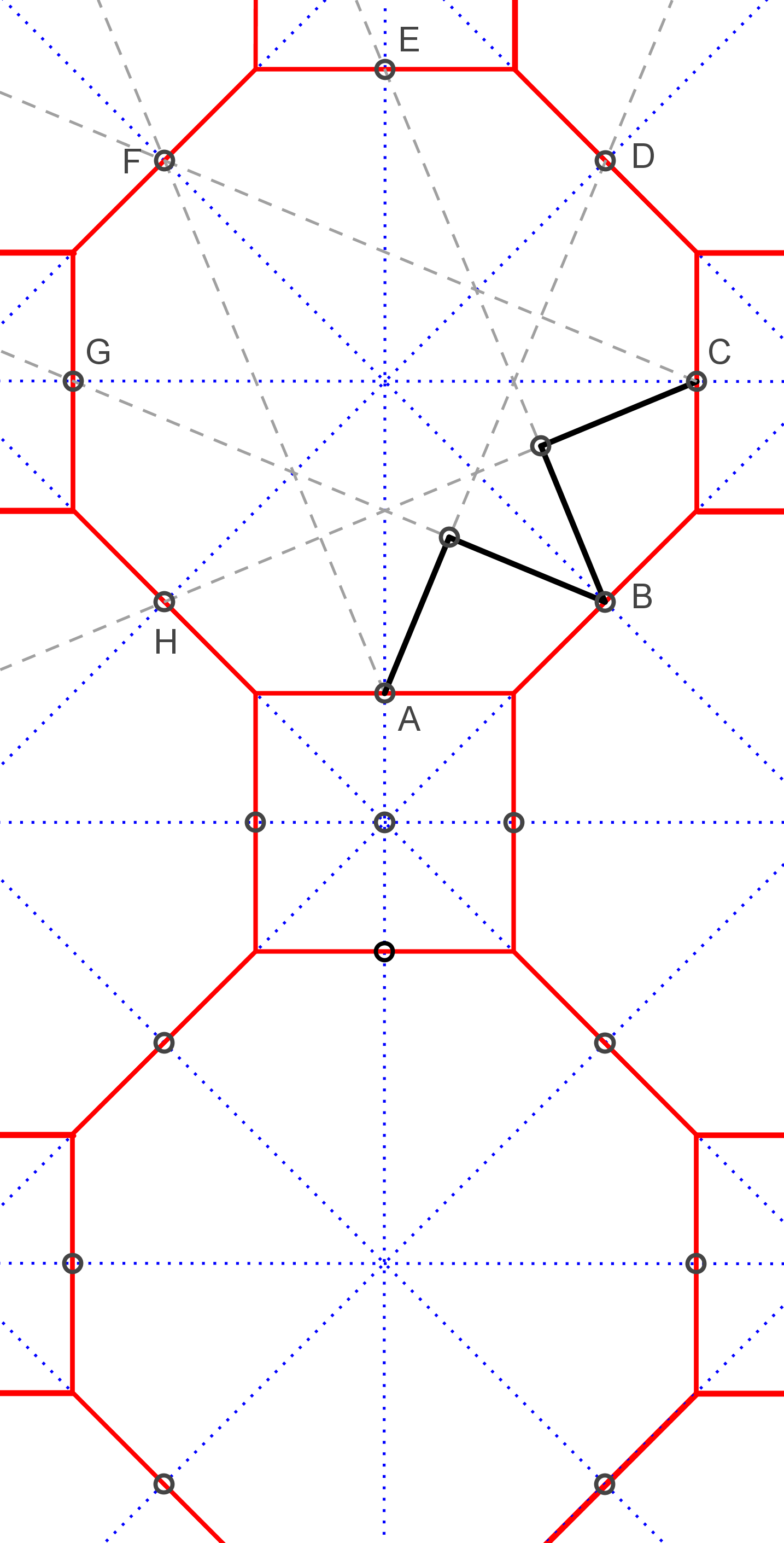
Gebruik een raster van tegen elkaar aan liggende veelhoeken die het hele vlak regelmatig bedekken. Hier is gekozen voor vierkanten en regelmatige achthoeken. De stippellijnen zijn symmetrieassen. De middens van alle zijden zijn aangegeven met een klein cirkeltje. Deze worden gebruikt voor het mozaïekontwerp.

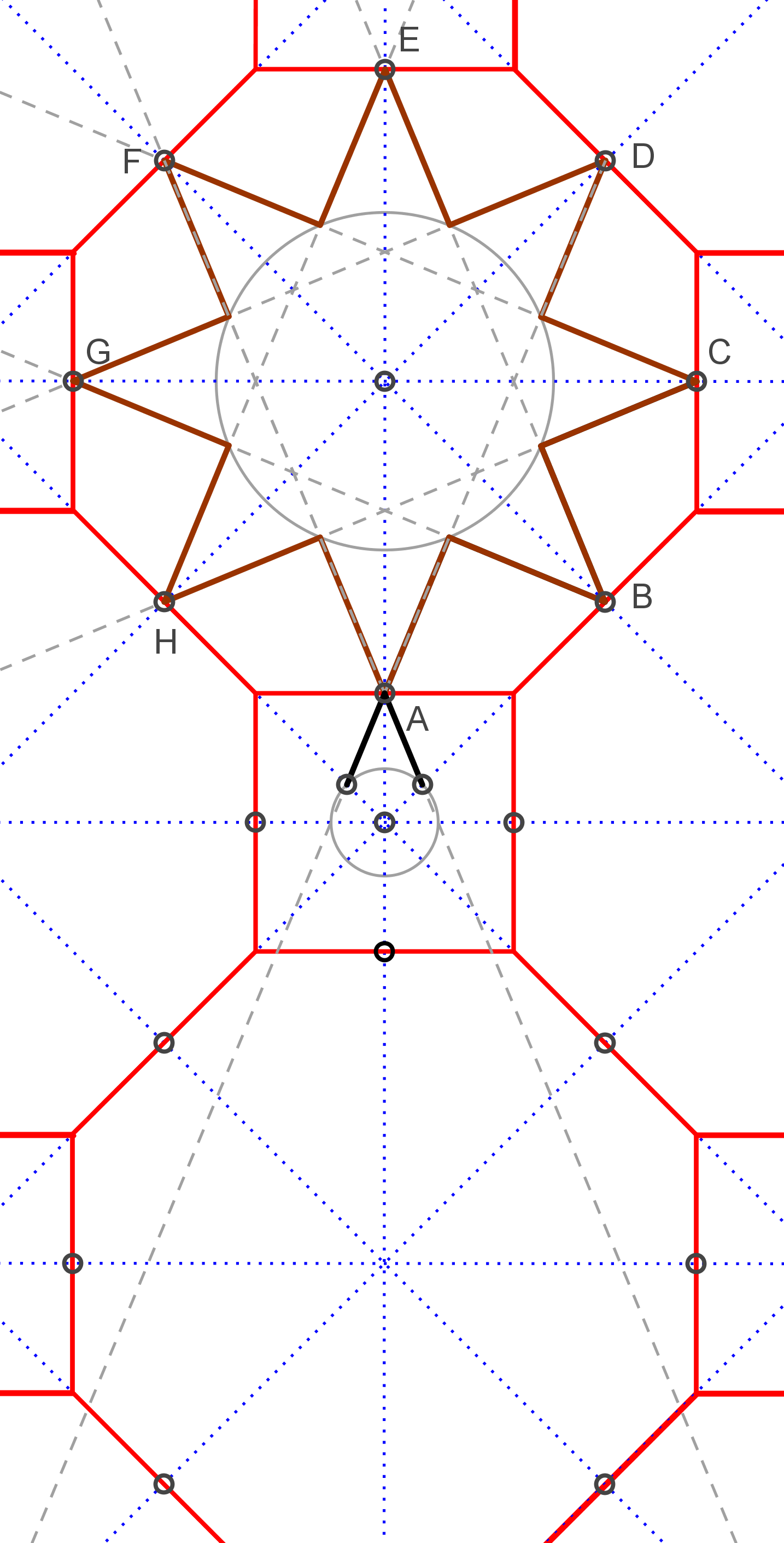
Begin met het tekenen van een ster in een achthoek. Je hebt hier de keus om de sterpunt heel stomp of juist heel scherp te maken. Bij het kiezen van de sterpunthoek wordt gekeken naar het hele raster; de hoek moet mooi passen in het geheel. Hier is gekozen voor vrij scherpe punten, met lijnen die richting het midden van de schuintegenoverliggende zijde lopen.	Teken de ster af, gebruik de cirkel als hulpmiddel om de juiste lijnen te tekenen. Verleng vervolgens de lijnen DA en FA naar beneden om de aansluitende vierpuntige ster te tekenen.	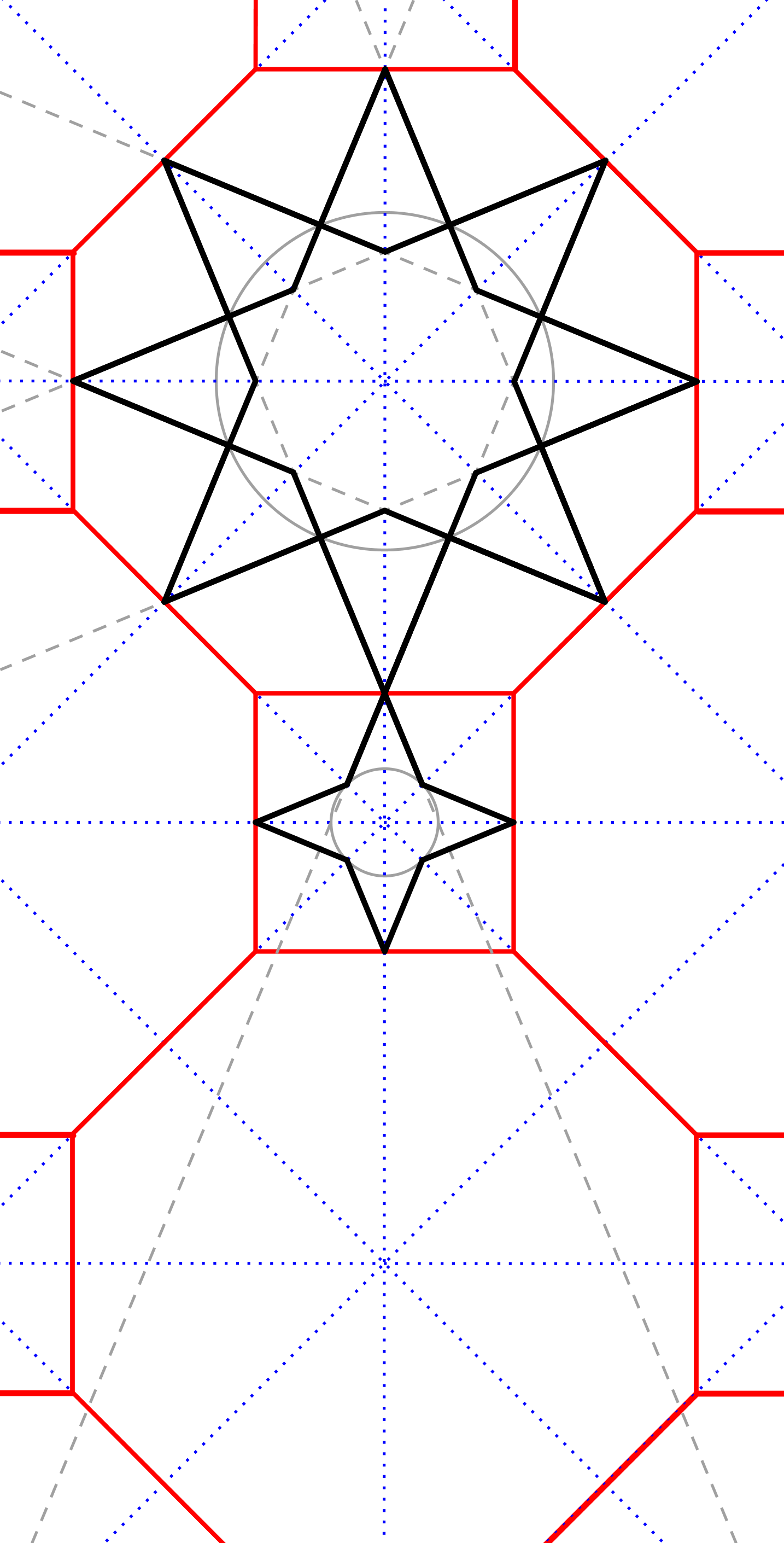Maak de vierpuntige ster af, gebruik hierbij eventueel een kleine hulpcirkel. Omdat de vierpuntige ster in verhouding tot de achtpuntige ster klein is, is er ook een kleinere achtpuntige ster in de grote geconstrueerd. Dit is gedaan door lijnstukjes naar binnen toe te verlengen zodat ook vliegervormen ontstaan. Zo komt er meer evenwicht in het ontwerp. Nu zijn zowel de achthoek als het vierkant ingevuld met sterren. Het basisontwerp is in principe klaar!

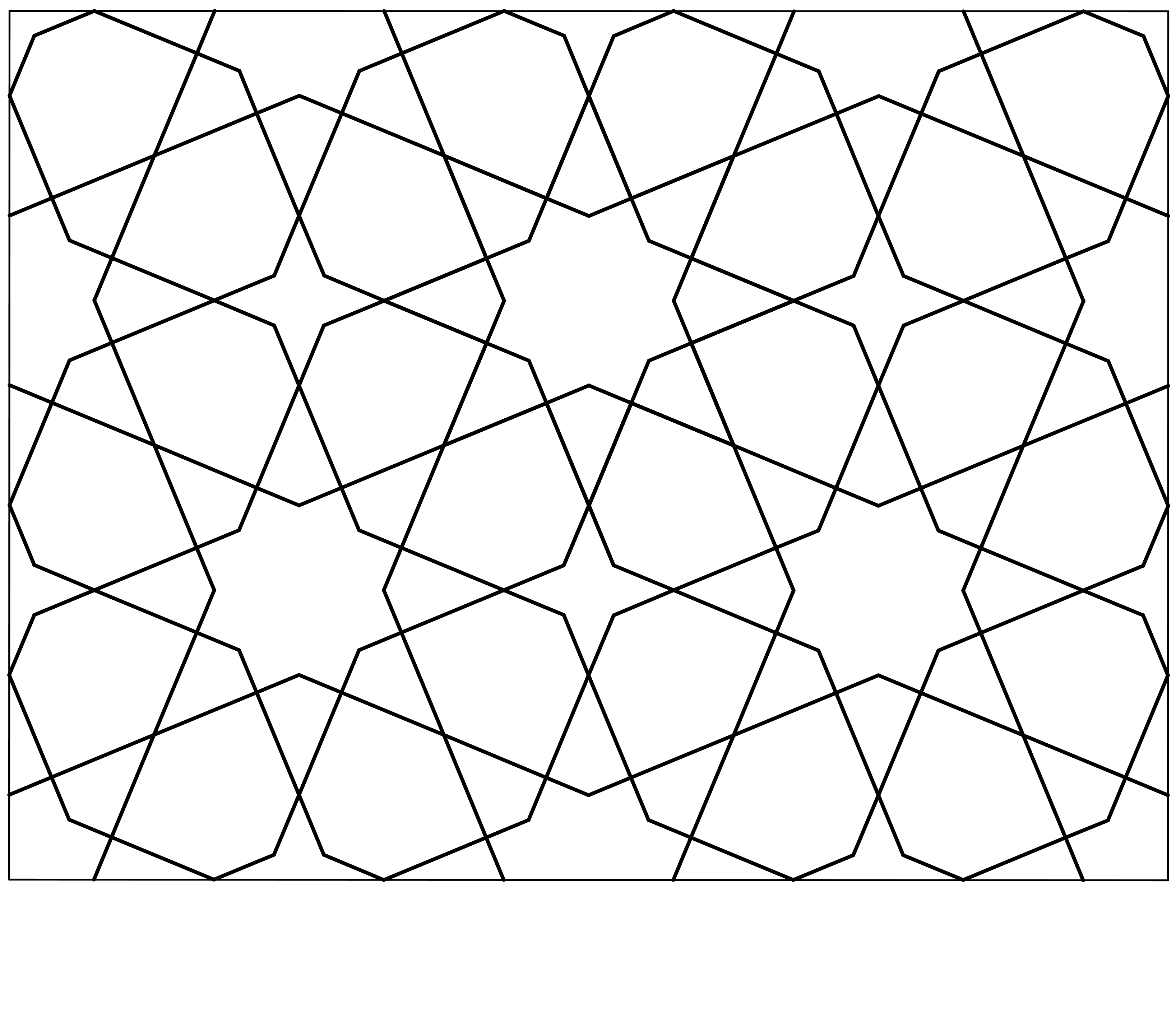
Je begint altijd met een regelmatig patroon van tegen elkaar aanliggende veelhoeken, meestal met allemaal zijden van gelijke lengte. We noemen dit een raster. In figuur 4a zie je een voorbeeld: Een raster van regelmatige achthoeken en vierkanten. Let op: Een raster is niet meer zichtbaar in het uiteindelijke mozaïek! In de figuren 4b t/m g wordt uitgelegd hoe je vanuit een raster tot een mozaïekontwerp komt.

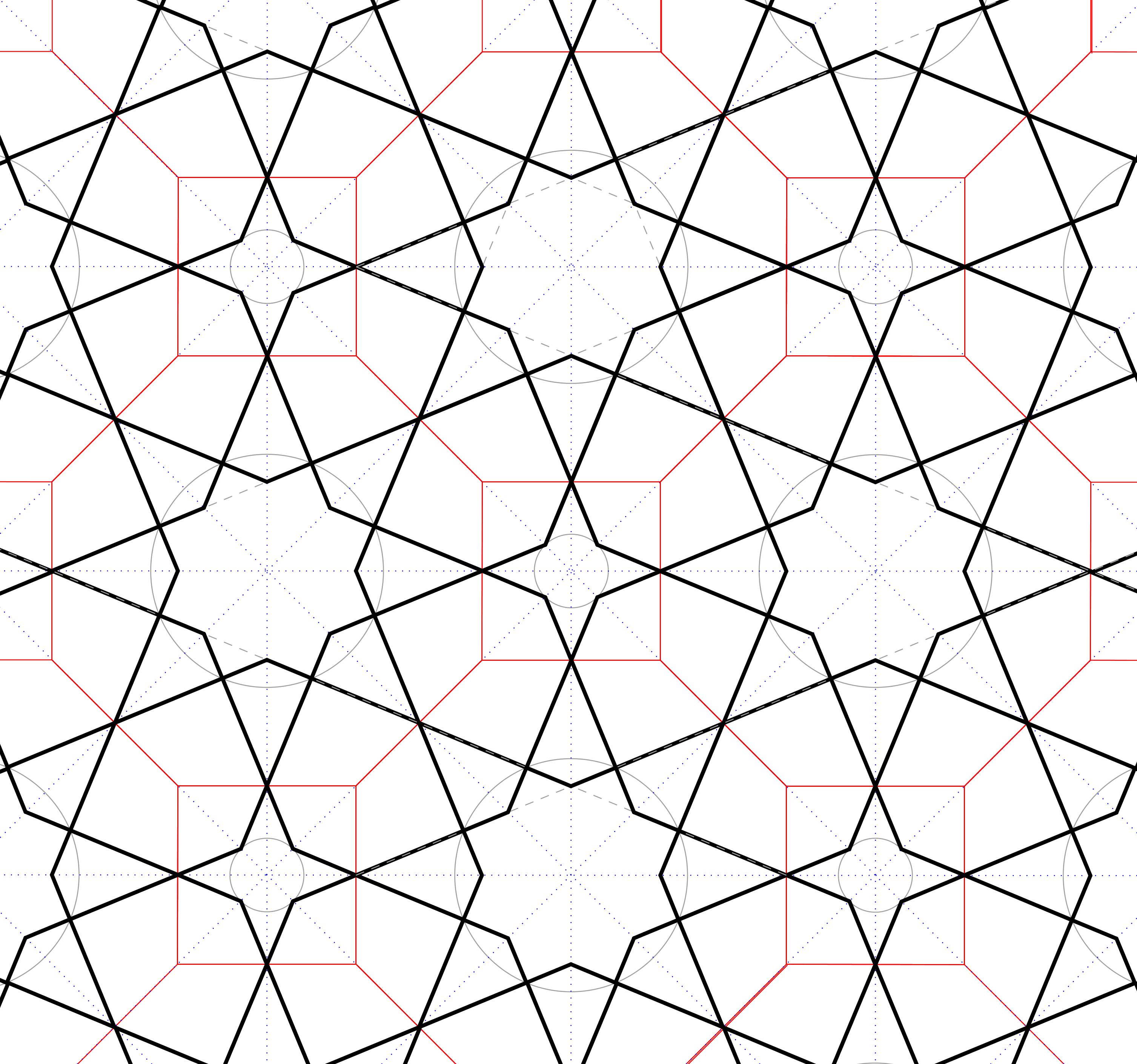
Dezelfde sterren worden op alle achthoeken en vierkanten getekend door lijnen te verlengen, hulpcirkels te tekenen enzovoort. Je kunt het ontwerp ook overtrekken op een nieuw blad, of alle hulplijntjes uitgummen zodat het mozaïek mooi op de voorgrond komt.	Er wordt een omlijsting gekozen langs symmetrielijnen. Je kunt bij dit raster ook diagonale symmetrielijnen gebruiken en het ontwerp 45° kantelen (figuur g). Door vlakken te kleuren als op een schaakbord krijgen de grenslijnen minder, en de vlakvormen juist meer nadruk. Zo ontstaat een totaal andere indruk van het patroon.

Hoe komt het, dat deze ontwerptechniek zo succesvol was (en is)? Daar zijn verschillende redenen voor. Ten eerste leidt de techniek altijd tot een patroon met ‘kruispunten’ en zonder ‘driesprongen’, waardoor de lijnen over het hele tableau, zonder onderbreking, lijken door te lopen, hetzij in een soort van ‘kring’, hetzij in een zich regelmatig herhalende, hoekige golfbeweging, die in twee richtingen doorloopt. Dit ‘lijnenspel’ geeft esthetisch een mooi beeld aan het patroon en draagt bij aan een suggestie van oneindigheid. Het bood de ontwerpers ook de mogelijkheid om nóg mooiere mozaïeken te maken; mozaïeken die een driedimensionaal effect geven dankzij de zogenaamde weeftechniek. Bij deze techniek maak je van alle lijnstukken tussen de vormen bredere strookjes door ze te verdubbelen: in plaats van een lijn teken je twee parallelle lijnen. Door vervolgens de strookjes bij kruispunten te onderbreken lijkt het alsof de ene strook over de andere heen loopt. In het volgende nummer van Pythagoras wordt uitgelegd hoe je dit in je eigen tekening kunt doen.

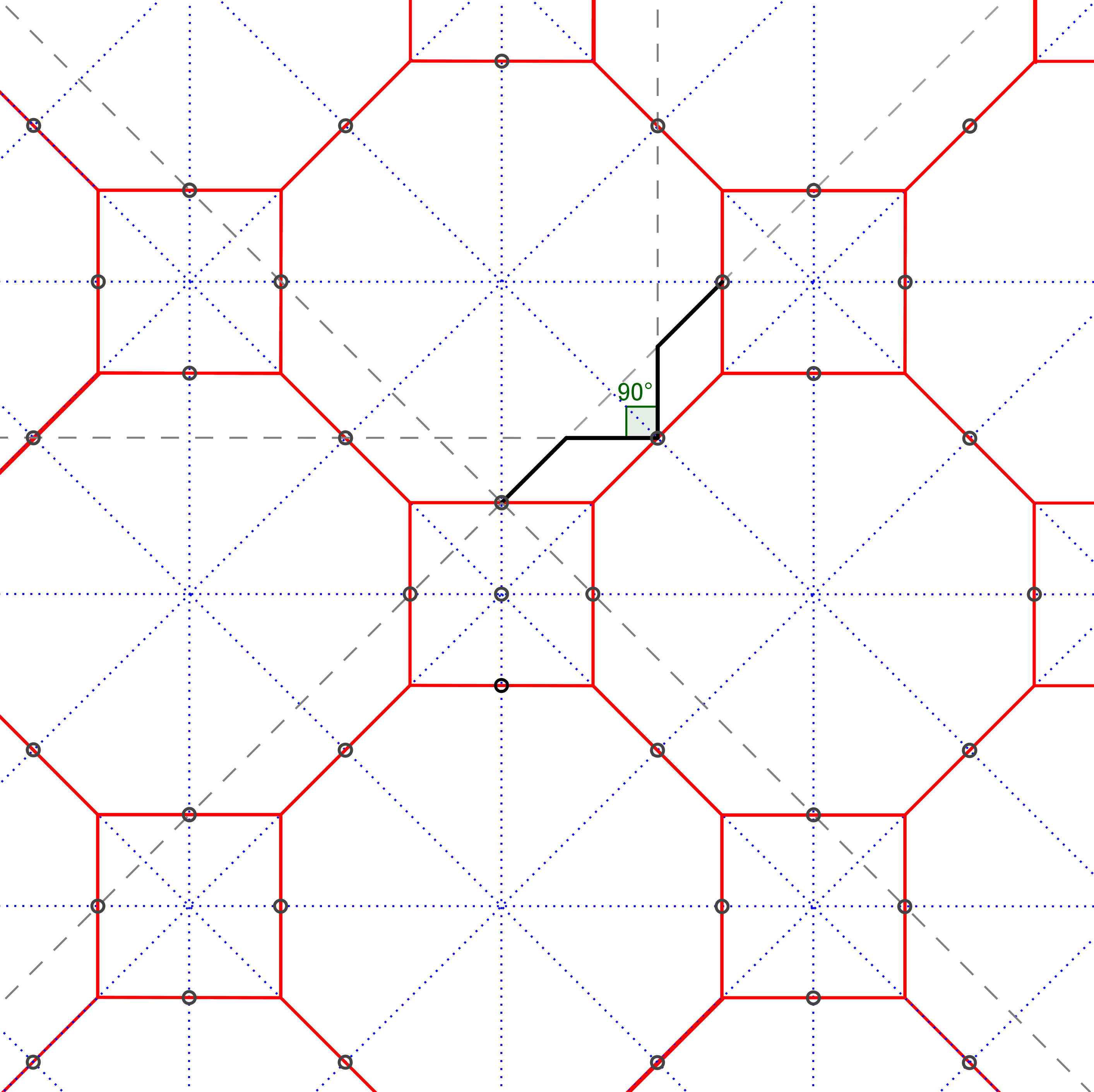
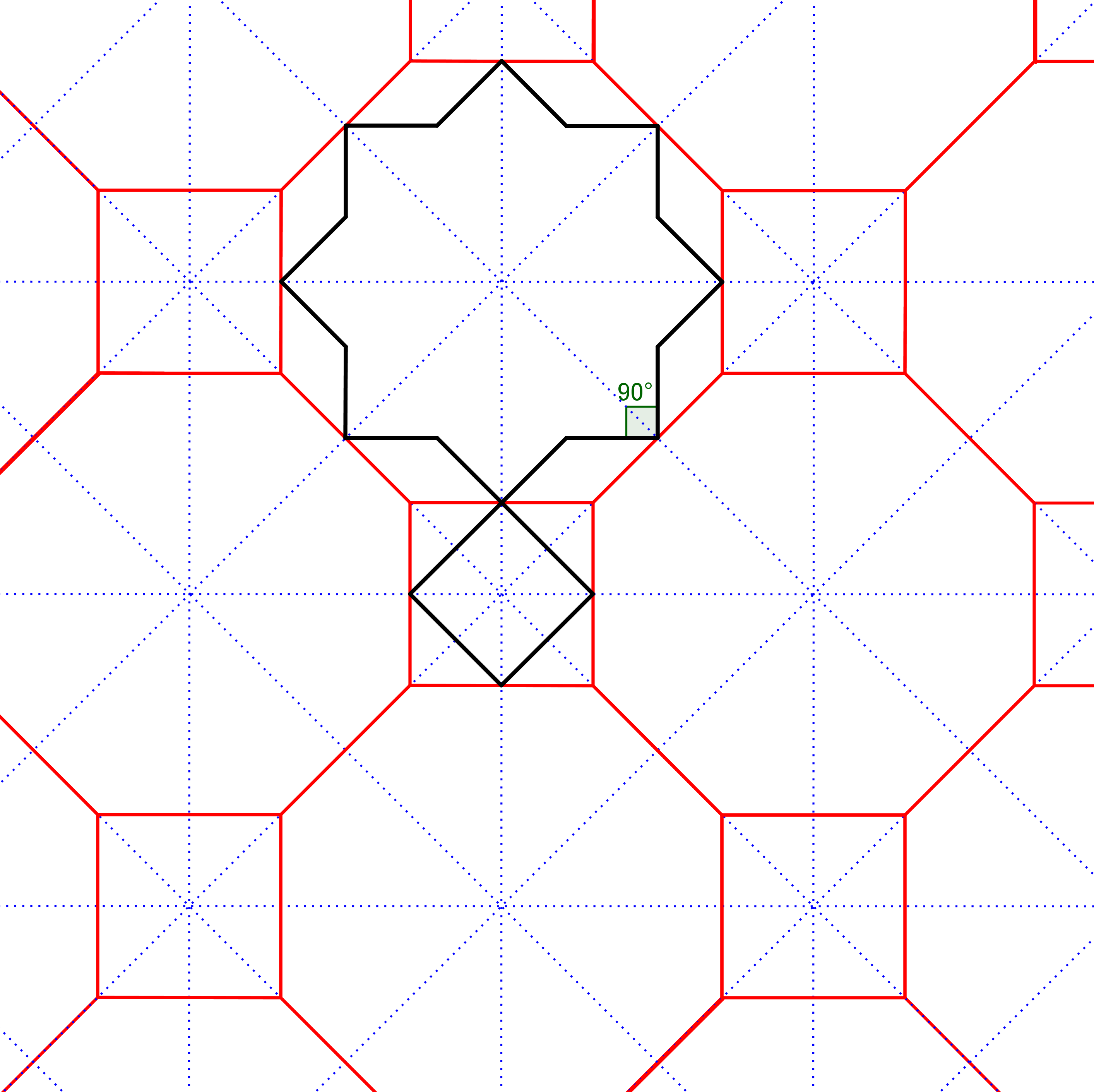
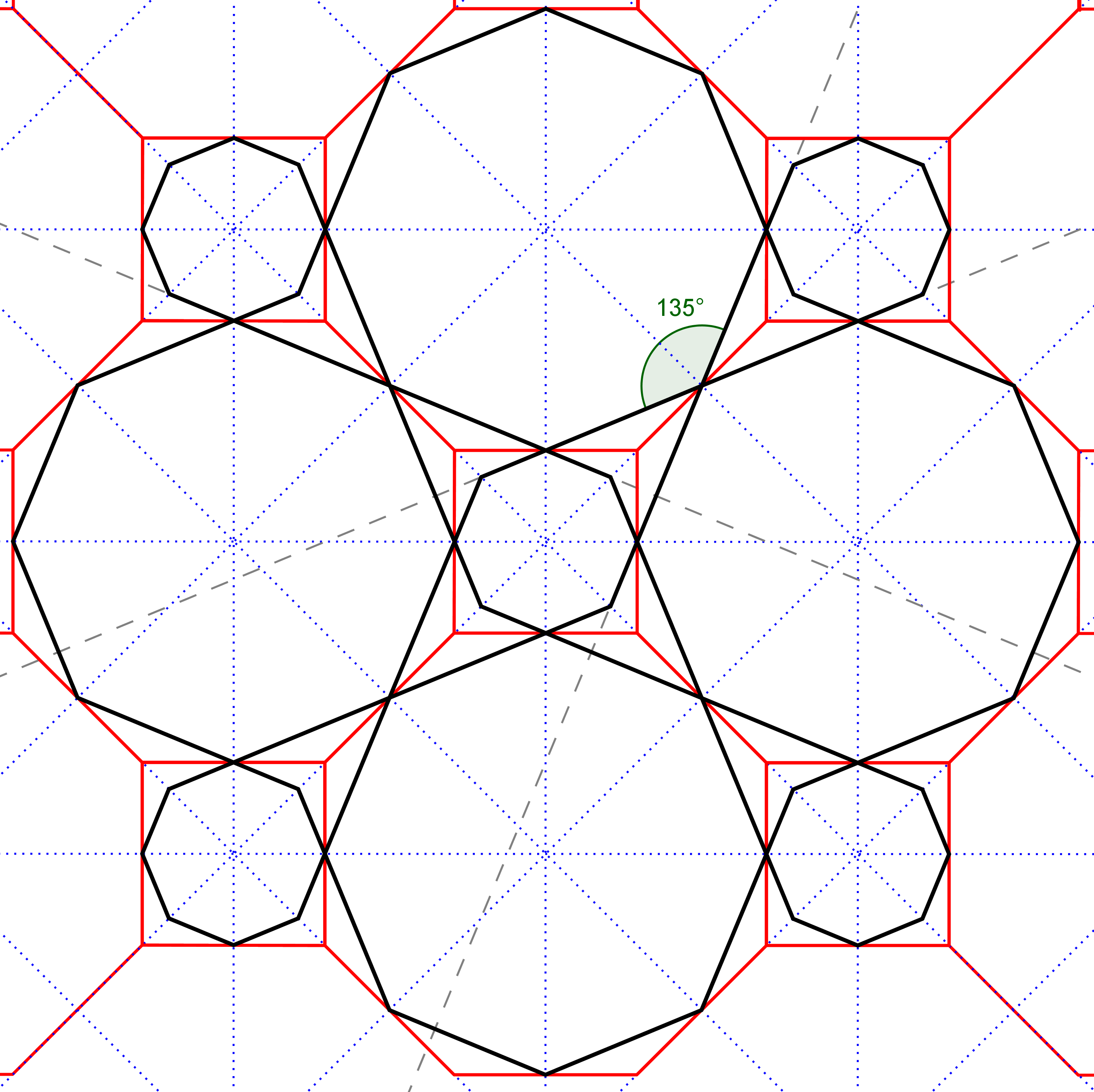
Een tweede reden voor succes is, dat men met eenzelfde raster veel verschillende mogelijkheden heeft om een patroon te maken. Vaak zijn de eindresultaten zo verschillend, dat alleen kenners kunnen zien dat hetzelfde raster gebruikt is. Je kunt namelijk ook starten met een andere hoek van de sterpunten! In figuur 4b was een scherpe hoek van 45° gekozen. Een rechte hoek (90°) kan ook, zie figuur 5. Of een stompe hoek (in dit voorbeeld 135°), zie figuur 6. Figuur 5 laat ook zien hoe je in een basisontwerp aanpassingen kunt maken, of lijnen kunt toevoegen zodat een complexer patroon ontstaat. Maar dit is niet zo eenvoudig! Om dit zelf goed te kunnen doen heb je veel ervaring nodig en moet je veel bestaande mozaïeken bestuderen.

Op hetzelfde rode raster kun je ook hoeken van 90° construeren vanuit de middelpunten van de zijden. Dan ontstaan achtpuntige sterren met rechte hoeken, en vierkantjes. Ga je dit uitbreiden, dan ontstaat een patroon dat uit drie geometrische vormen bestaat
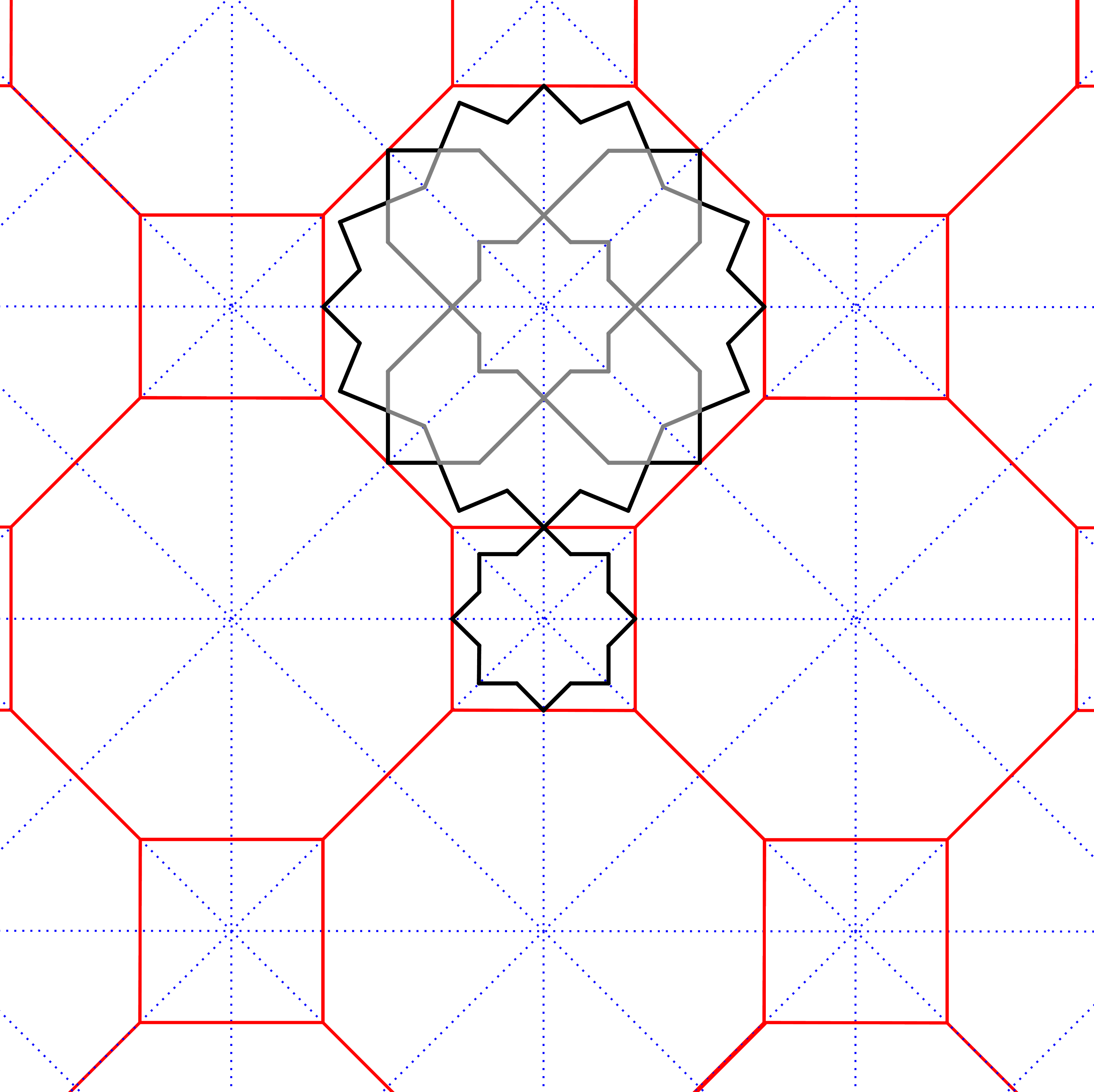
Het patroon kan ook op allerlei manieren complexer worden gemaakt. In dit voorbeeld zijn hiertoe dezelfde achtpuntige ster en hetzelfde vierkant opnieuw getekend, maar nu iets gedraaid, zodat een zestienpuntige ster en een achtpuntige kleinere ster ontstaan. Vervolgens worden wat lijnstukjes gewist en andere toegevoegd (5d), zodat in de zestienpuntige ster nieuwe vormen ontstaan. Merk op dat ervoor is gekozen om de kleine achtpuntige ster opnieuw te gebruiken in de zestienpuntige ster. Verder valt op dat alle vormen spiegelsymmetrisch zijn. Zo ontstaat een evenwichtig patroon dat voldoet aan de traditionele ontwerpregels.

Een langs symmetrieassen omkaderd eindresultaat. Om dit te bereiken is nog een extra ster toegevoegd in het ontwerp van figuur 5d, waardoor de bruine vormen en de witte vierkantjes ontstaan. Het ontwerp is vervolgens een paar keer gedupliceerd en alle hulplijntjes zijn gewist. Door de inkleuring worden de vormen benadrukt. Tegelijk blijft het lijnenspel goed zichtbaar doordat de lijnen vrij dik getekend zijn.

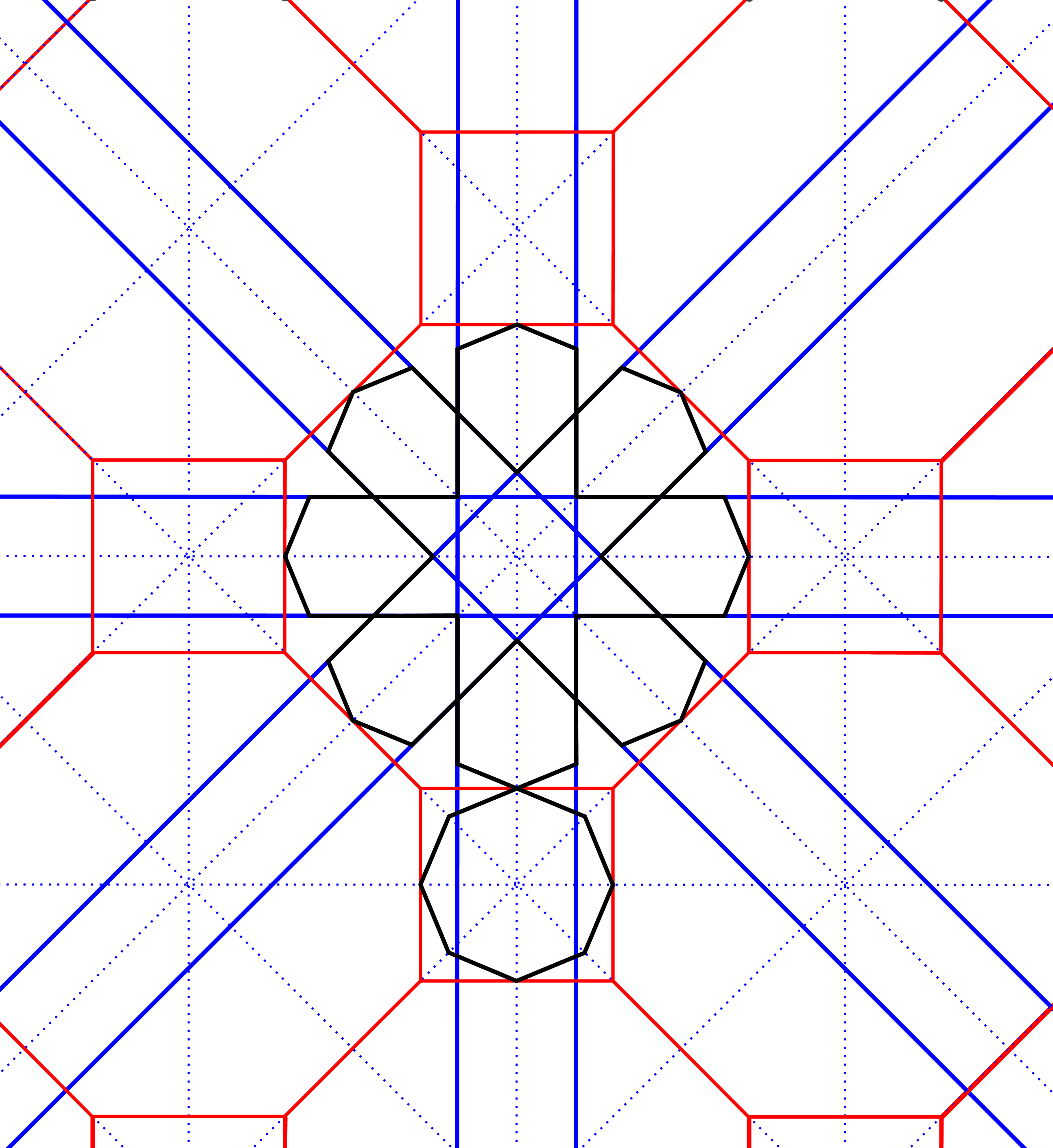
Hier is voor een stompe hoek van 135° gekozen waardoor geen sterren, maar grote en kleine regelmatige achthoeken ontstaan, omringd door pijlpuntvormpjes. Ook hier kan het ontwerp complexer worden gemaakt. Grote regelmatige veelhoeken worden vaak omgetoverd tot rozetten. Dit is gedaan in figuur b door paren blauwe parallelle lijnen te trekken die telkens loodrecht op twee zijden van de rode achthoek staan. Er ontstaat een rozet: Een kleinere ster, omringd door zeshoekige bloemblaadjes.		Een gekleurd en omkaderd eindresultaat met blauwe achtpuntige sterren en achthoeken, met witte vliegers en vijfpuntige sterren en bruine zeshoekige ‘bloemblaadjes’. Doordat de lijnen gewist zijn, trekken de vormen meer de aandacht

De ontwerptechniek is dus heel breed toepasbaar en kan ook rekening houden met het gebruikte materiaal bij het uiteindelijke tableau. Immers; wanneer bijvoorbeeld een reliëf gestuukt wordt, dan zijn er weer hele andere mogelijkheden dan wanneer de vormpjes allemaal apart uit geglazuurde tegels worden gehakt om vervolgens te worden samengesteld tot een kleurrijk tableau. In het laatste geval kun je bijvoorbeeld onmogelijk heel scherpe hoekpunten toepassen. Een hoek van minder dan 30° is heel lastig om uit te hakken.

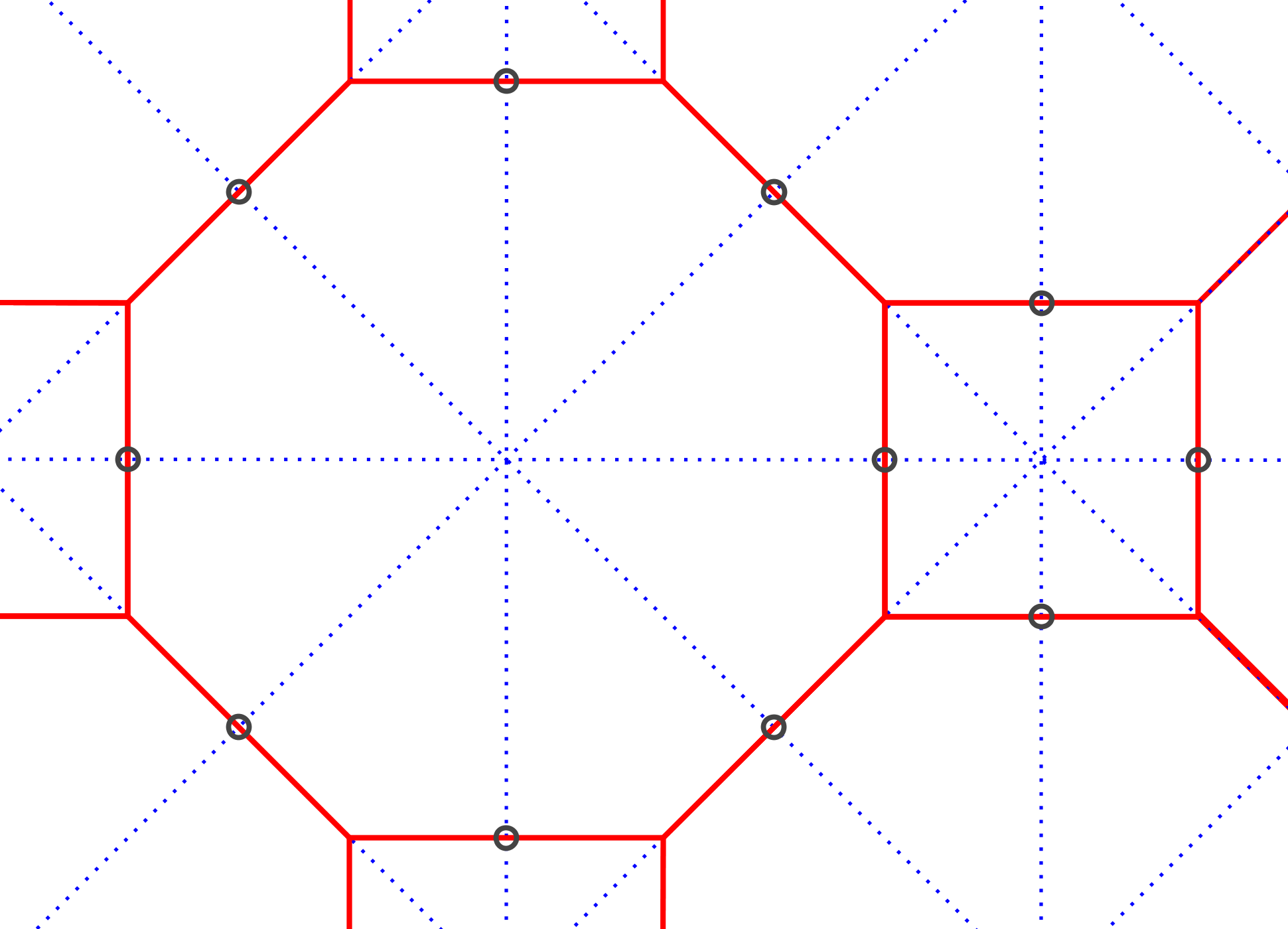
Het raster van figuur 4 nogmaals afgebeeld, op groter formaat, om te gebruiken als werkblad. Je kunt nu zelf de stappen van figuur 4b t/m f uitvoeren. Maar je kunt het ook gebruiken om andere patronen te ontwerpen, zoals die in figuur 5 en 6.

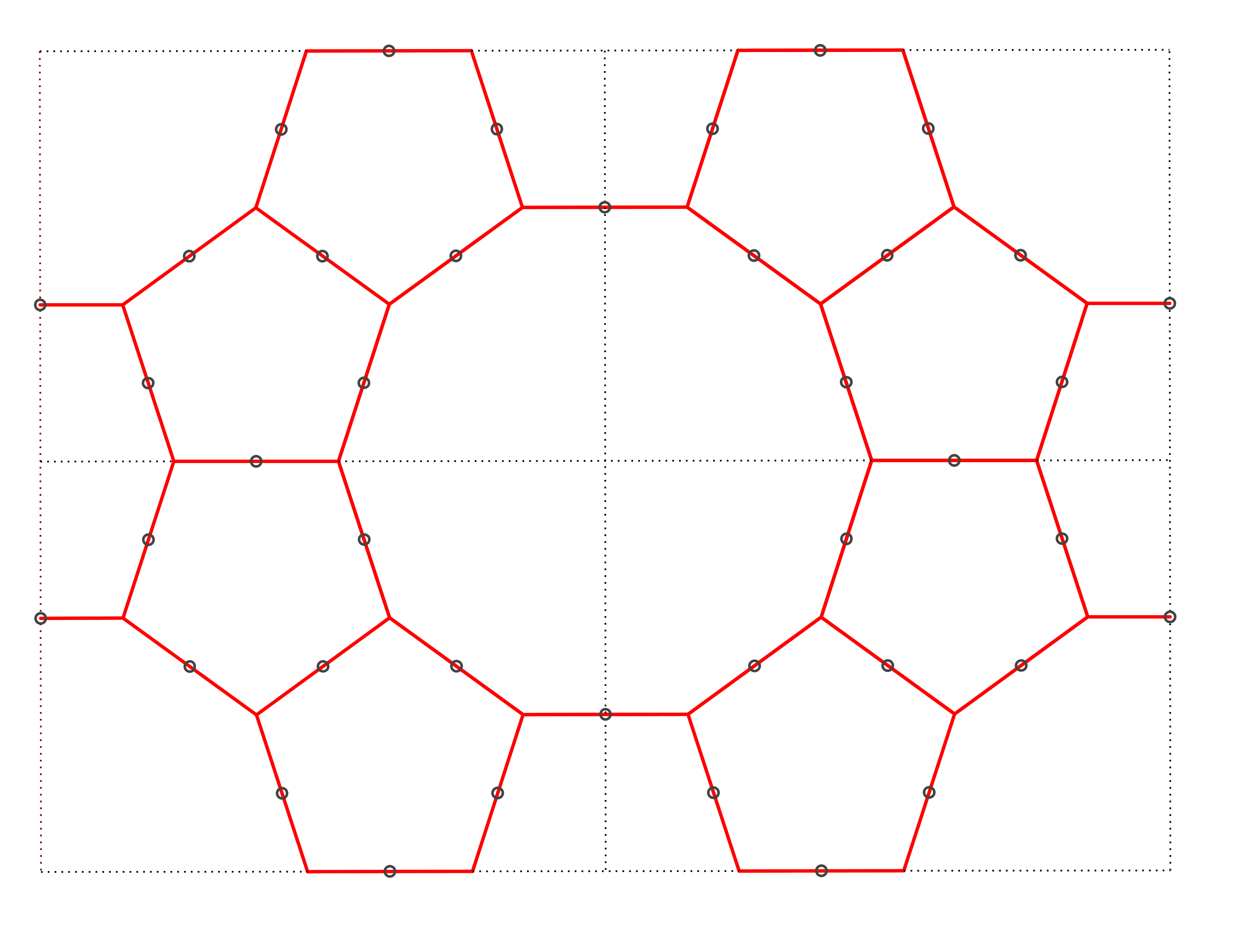
Een nieuw raster waarmee tienpuntige sterren, gecombineerd met vijfpuntige, in een regelmatig patroon kunnen worden ontworpen. In de rode zeshoeken, waarvan je er links, rechts, boven en onder telkens een halve ziet, ontstaat een bijzondere vorm.

Hoe kun je nu zelf aan de slag gaan? In figuren 7 en 8 zie je twee rasters waarmee je zelf een mozaïek kunt ontwerpen. Maak je ontwerp direct op de figuur of gebruik dun papier of overtrekpapier dat je met paperclips op het raster vastmaakt. Kies één van de ontwerpopties uit figuren 4, 5 en 6 en probeer het uit! Ben je tevreden met je ontwerp, dan kun je dit weer herhaaldelijk overtrekken op een groter stuk papier, bijvoorbeeld van A3- of A2-formaat. Je kunt je mozaïek zo groot maken als je zelf wilt. Maak hierbij gebruik van de schuif- en draaisymmetrie: Door je eigen ontwerp telkens door te schuiven over het papier, of te draaien, en weer over te trekken breid je het patroon uit.

Vaak zal het mozaïek dat je ontwerpt eeuwen geleden al gemaakt zijn, misschien wel door een Marokkaanse ontwerper op een werkplaats in een bazaar van Fes! Op de site tilingsearch.com zou je dit zelf kunnen onderzoeken. Op deze site staan honderden verschillende patronen met verwijzingen naar locaties waar deze zijn toegepast in een mozaïek.

Het mooist is natuurlijk als je je eigen ontwerp ook inkleurt. Je kunt de grotere vormen ook invullen met bloemmotieven of een versiering langs de randen van het mozaïek maken. Voor inspiratie kun je gaan browsen op www.patterninislamicart.com, daar zie je heel veel voorbeelden van hoe de patronen oorspronkelijk werden uitgevoerd. Maar nóg mooier is het natuurlijk om ze met eigen ogen te bekijken! Dat kan misschien in een moskee bij je in de buurt, of tijdens een vakantie in Spanje, in het beroemde Alhambra bijvoorbeeld, of op talloze plaatsen in Marokko, Turkije, Egypte, Iran, Tunesië enzovoort.

Wat kun je in het volgende artikel verwachten? Naast de al genoemde ontwerptechniek voor het aanbrengen van een weefeffect, maak je kennis met nog een andere ontwerpmogelijkheid. Verder worden fascinerende andere rasters besproken, die honderden jaren geleden in het Midden-Oosten werden bedacht. Hiermee kun je nog meer schitterende mozaïeken ontwerpen.

Maite Karssenberg schrijft in het boek “Snijpunt Isfahan” over de reis die zij en haar vader Goossen maken naar Isfahan, het centrum van de Perzische mozaïekkunst. Daar komen verschillende werelden samen: die van ouder en kind, die van bèta en alfa, die van rationaliteit en emotie en die van het Oosten en het Westen.

Pythagoras mag drie exemplaren van dit boek weggeven. Wil je kans maken? Stuur een mailtje naar [email protected].