
Het tapijt van Sierpinski
Heel eenvoudige wiskunde kan soms prachtige beelden opleveren. Een goed voorbeeld daarvan is het tapijt van Sierpiński, vernoemd naar de Poolse wiskundige Wacław Sierpiński. Je kunt de figuur eenvoudig zelf maken op ruitjespapier.

Figuur 1
Maak eerst een rij met allemaal enen. Zet ook allemaal enen in de meest linkse kolom. Je krijgt dan figuur 1. Vervolgens ga je alle nog lege hokjes invullen van links naar rechts en van boven naar beneden. Je doet daarbij telkens de volgende berekening: tel de getallen links van het hokje, boven het hokje en linksboven het hokje bij elkaar op. Deel deze som door drie en noteer de rest.
Bijvoorbeeld: $2 + 1 + 2 = 5,$ na deling door drie blijft er twee over. Ga zo door totdat alle hokjes zijn ingevuld. Hokjes waar je het cijfer nul invult, kleur je zwart. Als je geen rekenfouten maakt, krijg je de afbeelding zoals in figuur 2.

Figuur 2
Natuurlijk kun je de figuur op een groter ruitjesblad maken. Je zult zien dat het patroon zich eindeloos blijft herhalen zoals in figuur 3.

Figuur 3
Hulp van de computer
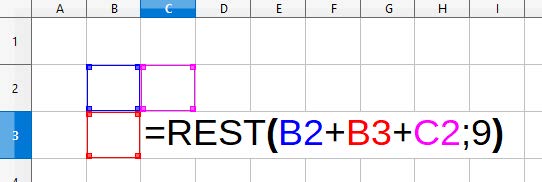
Figuur 4
We kunnen het onszelf natuurlijk een beetje gemakkelijker maken door gebruik te maken van een spreadsheet, zoals LibreOffice of Excel. Ook kunnen we eens kijken wat er gebeurt als we delen door een ander getal dan drie. In dit voorbeeld kiezen we voor negen. Typ in cel C3 de formule =REST(B2+B3+C2;9) in (figuur 4). Deze doet precies wat we eerder met de hand berekenden. Kopieer vervolgens de formule in een groot vierkant met cel C3 in de linkerbovenhoek. Je krijgt dan een groot veld met alleen maar nullen (figuur 5).
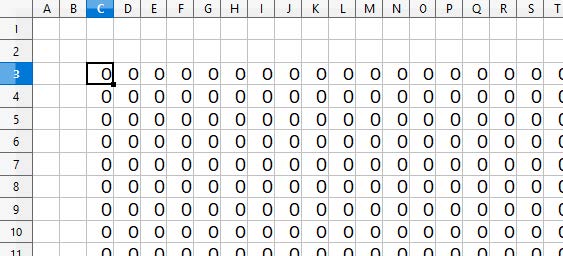
Figuur 5
Daarna vervang je de formule in cel C3 door het cijfer één. De spreadsheet zal onmiddellijk alle overige waarden van het tapijt van Sierpiński berekenen (figuur 6).
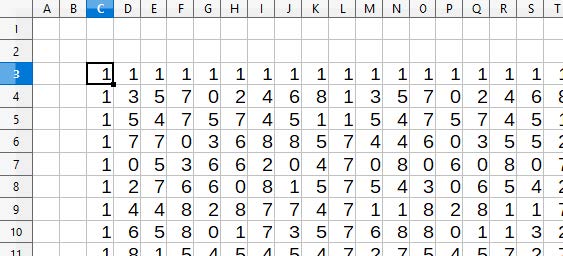
Figuur 6
Tot slot maak je gebruik van een handige functie onder de naam ‘voorwaardelijke opmaak’. Selecteer alle cellen en geef deze een voorwaardelijke opmaak, zodanig dat de achtergrond bijvoorbeeld rood wordt als de cel de waarde nul heeft. Onmiddellijk krijg je figuur 7 te zien.

Figuur 7
Wil je verder experimenteren, vervang de formule dan door =REST(B2+B3+C2;\$A\$1) en zet in cel A1 het getal waardoor je wilt delen. Voor verschillende waarden van cel A1 krijg je verschillende tapijten. Daarbij zijn priemgetallen (zoals drie) of machten van een priemgetal (zoals negen) waarden die mooie patronen opleveren. Hieronder vier afbeeldingen van 500 bij 500 cellen met verschillende delers.

Deling door 7

Deling door 17

Deling door 25

Deling door 27
