In Pythagoras wordt een hoop geschreven over getallen, hier is immers veel leuks over te vertellen. Alleen al over de natuurlijke getallen is een heleboel te zeggen. We kunnen kijken naar de bijzondere eigenschappen die getallen hebben, bijvoorbeeld de eigenschap dat een getal een priemgetal is, of dat het in de rij van Fibonacci getallen valt. De kleinste getallen op het begin van de getallenlijn zijn allemaal om een of andere reden interessant, danwel omdat het een kwadraat is, een priemgetal, een perfect getal of een Fibonaccigetal. Is dit als we wat verder op de getallenlijn kijken ook nog zo, of bestaan er ook oninteressante getallen? We kunnen 'bewijzen' uit het ongerijmde dat dit laatste niet het geval is! Stel namelijk dat die wel bestaan, dan moet er ook een kleinste zijn en die is dan op zichzelf interessant! Dat geeft een tegenspraak en zo weerleggen we het bestaan van oninteressante getallen. Maar welke getallen zijn dan interessanter dan anderen? Wat is nou eigenlijk de interessantheid van getallen?

Wat is de definitie van interessantheid?

De vraag is dus wat de interessantheid van getallen is. Uiteraard is het interessant zijn van een getal subjectief, we zullen niet allemaal dezelfde getallen even mooi vinden. Maar zelfs als we uitgaan van een mening over welke getallen wel of niet
interessant zijn en welke interessanter zijn dan anderen, kunnen we hier wiskundig wel iets nuttigs over zeggen. We kunnen proberen om een definitie van interessantheid te geven. Zelf heb ik een aantal uur uit het raam zitten staren en ben nu met volgende gekomen. We beschouwen enkel interessantheid binnen de natuurlijke getallen $\mathbb{N} = \{1, 2, 3, \ldots \}$, dus we kijken nu bijvoorbeeld niet naar het getal $\pi$.

Als we interessantheid willen bestuderen, hebben we allereerst een idee nodig van welke eigenschappen we interessant vinden. Zoals gezegd verschilt dit natuurlijk per persoon. Wellicht vind je het zelf ontzettend interessant als een getal geschreven kan worden als een som van twee kwadraten. Het zou kunnen dat die eigenschap mij koud laat en ik veel liever priemgetallen zie. Uiteindelijk zijn we hier vrij in en dit is ook zeker iets waar we in de definitie van interessantheid
keuzevrijheid in zullen hebben. Er is dus helemaal geen eenduidige verzameling van interessante eigenschappen. Ieder mag dit voor zichzelf kiezen. Je mag bijvoorbeeld zeggen dat je enkel naar de eigenschap dat een getal een priemgetal is
en de eigenschap dat een getal kwadratisch is wil kijken. In dat geval heeft jouw verzameling van interessante eigenschappen dus twee elementen.

Om dit wat duidelijker te maken en om hier wiskundig wat over te zeggen moeten we maar eens wat notatie introduceren. Ten eerste voor die verzameling van interessante eigenschappen, die we de interessantheidsverzameling noemen. Het is leuk om die alvast een symbool te geven, zeg $E$ (de $E$ van 'Eigenschap', binnen de wiskunde mogen we soms best lui zijn met notatie bedenken). In het voorbeeld dat we alleen naar de eigenschappen priem en kwadratisch kijken hebben we dus dat 

$$E = \{\mbox{priem}, \mbox{kwadratisch}\}$$

Nu hebben we dus een manier om onze verzameling van interessante eigenschappen aan te duiden, maar hoe kunnen we hier mee rekenen? Daar hebben we wel wat meer voor nodig. Ten eerste is het misschien handig om elke eigenschap af te korten, anders wordt het wel veel schrijfwerk als we een verzameling met $100$ interessante eigenschappen willen bekijken. Voor de eigenschap dat een getal een priemgetal is, kunnen we bijvoorbeeld $P$ noteren en voor kwadratisch $K$. We krijgen dan dat 

$$E = \{P, K\}$$

Let op: dit is dus maar een klein voorbeeld met specifiek deze twee eigenschappen, E mag natuurlijke veel meer interessante eigenschappen bevatten, bijvoorbeeld ook eigenschappen die je zelf hebt bedacht.

Hier zal ik alvast een tabel toevoegen van afkortingen van eigenschappen die we veel gaan bekijken.

Eigenschap		Afkorting		Eerste paar getallen
Priemgetal		$P$		$2, 3, 5, 7, 11, \ldots$
Semi-priemgetal		$Sp$		$4, 6, 9, 10, 14, \ldots$
Kwadraat		$K$		$1, 4, 9, 16, 25, \ldots$
Fibonacci		$F$		$1, 2, 3, 5, 8, \ldots$
Driehoeksgetal		$D$		$1, 3, 6, 10, 15, \ldots$
Palindroom		$Pa$		$1, 11, 121, 2002, \ldots$
Perfect getal		$Pe$		$6, 28, 496, 8128, \ldots$
Mersenne getal		$M$		$3, 7, 31, 127, 8119, \ldots$
Tabel 1:afkortingen en voorbeelden van interessante eigenschappen die we in dit artikel beschouwen

Voor het rekenen kunnen we de eigenschappen in $E$ beschouwen als een soort functies, ik zal direct toelichten wat ik hiermee bedoel. Voor elk natuurlijk getal n willen we kunnen aangeven of deze aan een bijzondere eigenschap voldoet of niet. De situatie dat een getal wel voldoet kunnen we dan aanduiden met $1$ en de situatie dat dat niet zo is met $0$. Voor een eigenschap $e \in E$ (dit betekent dat $e$ een interessante eigenschap binnen $E$ is) en een getal $n \in \mathbb{N}$ noteren we dan $e(n) = 1$ voor de situatie dat $n$ de eigenschap $e$ heeft en $e(n) = 0$ voor de situatie dat $n$ niet de eigenschap $e$ heeft. Zo krijgen we bij de priem-eigenschap bijvoorbeeld dat $P(5) = 1$, want $5$ is een priemgetal en $P(6) = 0$, want $6$ is geen priemgetal. De elementen in $E$ kunnen we dus gebruiken als een soort indicatoren.

Nu moeten we alleen nog zorgen dat we voor elke eigenschap in $E$ kunnen aangeven hoe interessant we die eigenschap vinden. Dit is opnieuw voor iedereen anders. Ik vind priemgetallen bijvoorbeeld erg interessant dus ik zal ze een hoog waarderen, maar misschien vindt mijn buurman ze helemaal niet zo interessant en zal hij ze een veel lagere waardering geven. Voor elke eigenschap in $E$ gaan we dit aangeven met een $W$ van waardering en in de index de eigenschap.
Dus als $e \in E$ een interessante eigenschap is, dan noteren we $W_e$ voor de waardering van $e$. Als ik nu vind dat een priemgetal waardering $10$ moet krijgen, dan noteer ik $W_P = 10$ en als mijn buurman ze zoals eerder gezegd lager waardeert, zeg met $6$, dan noteren we voor hem $W_P = 6$. Voor de waardering is dus iedereen vrij om een waarde te geven. Laten we echter wel afspreken dat deze tenminste $0$ moet zijn en reëel, dus in $\mathbb{R}_{\ge 0}$.

Nu komen we dan eindelijk toe aan het begrip van interessantheid. We gaan de totale interessantheid van een getal $n \in \mathbb{N}$ noteren als $I(n)$. De totale interessantheid van $n$ is dan dus de som van alle waarderingen van de eigenschappen waar $n$ aan voldoet. Omdat de elementen in $E$ eigenlijk indicatoren van interessante eigenschappen zijn, kunnen we dit makkelijk optellen als $e(n)W_e$ voor alle $e \in E$. We krijgen zo dus

$$I(n)=\sum_{e \in E}e(n)W_i$$

waarbij $\sum_{e \in E}$ staat voor "we tellen op over alle interessante eigenschappen in $E$". Laten we naar een voorbeeld kijken om dit allemaal wat meer voor ons te zien. We beschouwen de volgende interessantheidsverzameling:

$E=\{P, Sp, K, F, D, Pa\}$$

en ik geef ze de volgende waardering:

	$W_P = 10$		$W_F = 7$
	$W_{Sp} = 3$		$W_D = 2$
	$W_K = 4$		$W_{Pa} = 2$

Nu kunnen we met deze interessantheidsverzameling en deze gekozen waardering van de interessante eigenschappen de totale interessantheid van getallen berekenen. Om het klein te houden, bepalen we nu alleen de interessantheid van de getallen in het rijtje van $1$ tot en met $10$. Voor $1$ krijgen we

$$I(1) = P(1) \cdot W_P + Sp(1) \cdot W_{Sp} + K(1) \cdot W_K + F(1) \cdot W_F + D(1) +\cdot W_D + Pa(1) \cdot W_{Pa} \\
= 1 \cdot 0 + 0 \cdot 10 + 0 \cdot 3 + 1 \cdot 4 + 1 \cdot 7 + 1 \cdot 2 + 1 \cdot 2 = 15$$

We zien dus dat het getal $1$ interessantheid $15$ heeft. Voor de rest van de getallen krijgen we $I(2) = 19, I(3) = 21, I(4) = 9, I(5) = 19, I(6) = 7, I(7) = 12, I(8) = 9, I(9) = 9$ en $I(10) = 5$. In dit rijtje kunnen we dus zien dat $3$ het meest interessante getal is met totale interessantheid $21$. Het getal $10$ is daarentegen het minst interessante getal met slechts interessantheid $5$. 

Hier hebben we nog een vrij kleine interessantheidsverzameling bekeken. Voor nog meer eigenschappen kunnen we kijken op de website van de On-line Encyclopedia of Integer Sequences of korter OEIS. Als ik nu op de website kijk zie ik dat er $331942$ rijen op deze website staan en dat die zouden we allemaal kunnen opnemen in de interessantheidsverzameling! Het is wel de vraag hoe interessant we al die eigenschappen nu werkelijk vinden, dat is natuurlijk subjectief, maar er zal vast veel leuks bij zitten. Statistisch gezien zou zo’n grote verzameling aan interessante eigenschappen wel een stuk leuker zijn, omdat getallen zich nu veel meer gaan onderscheiden van elkaar en dan wordt het ineens bijzonder om het meeste interessante getal te zijn. Zou $3$ dan nog steeds het meest interessante getal zijn in het rijtje van $1$ tot en met $10$? Praktisch is dit helaas moeilijk uitvoerbaar, maar we zullen nog wel een statistische analyse doen met een kleinere verzameling van interessante eigenschappen.

Hoe meet je interessantheid?

We hebben al een voorbeeld gezien van hoe we interessantheid meten voor de getallen in het rijtje $1$ t/m $10$ met de eerder gekozen interessantheidsverzameling en waardering. Dit is echter maar een klein voorbeeld en hier kunnen we nog geen  hele goede conclusies uit trekken voor interessantheid bij de gegeven interessantheidsverzameling. Misschien is het wat leuker om naar de interessantheid van grotere verzamelingen getallen te kijken. Binnen zo'n deelverzameling van $\mathbb{N}$ kunnen we dan bijvoorbeeld de hoogste mate van interessantheid bepalen en bij welk getal die hoort, anders gezegd, welk(e) getal(en) in deze verzameling het meest interessant is (zijn)! Daarnaast kunnen we ook kijken wat de gemiddelde mate van  interessantheid is en nog meer van dat soort statistische eigenschappen. We beschouwen hier als voorbeeld de interessantheidsverzameling

$$E = \{P, K, F, D, Pa\}$$

waarbij voor het gemak semipriem is weggelaten ten opzichte van het eerdere voorbeeld tot en met $10$. We hanteren dezelfde waardering. Omdat ik net wat te weinig tijd en koffie heb om dit allemaal met de hand te doen, heb ik een aantal programma’s geschreven om grafieken mee te maken en berekeningen mee te doen. Eerst eens twee grafieken. Hoe ziet interessantheid er nou bijvoorbeeld uit als we tot $100$ of zelfs tot $1000$ kijken?

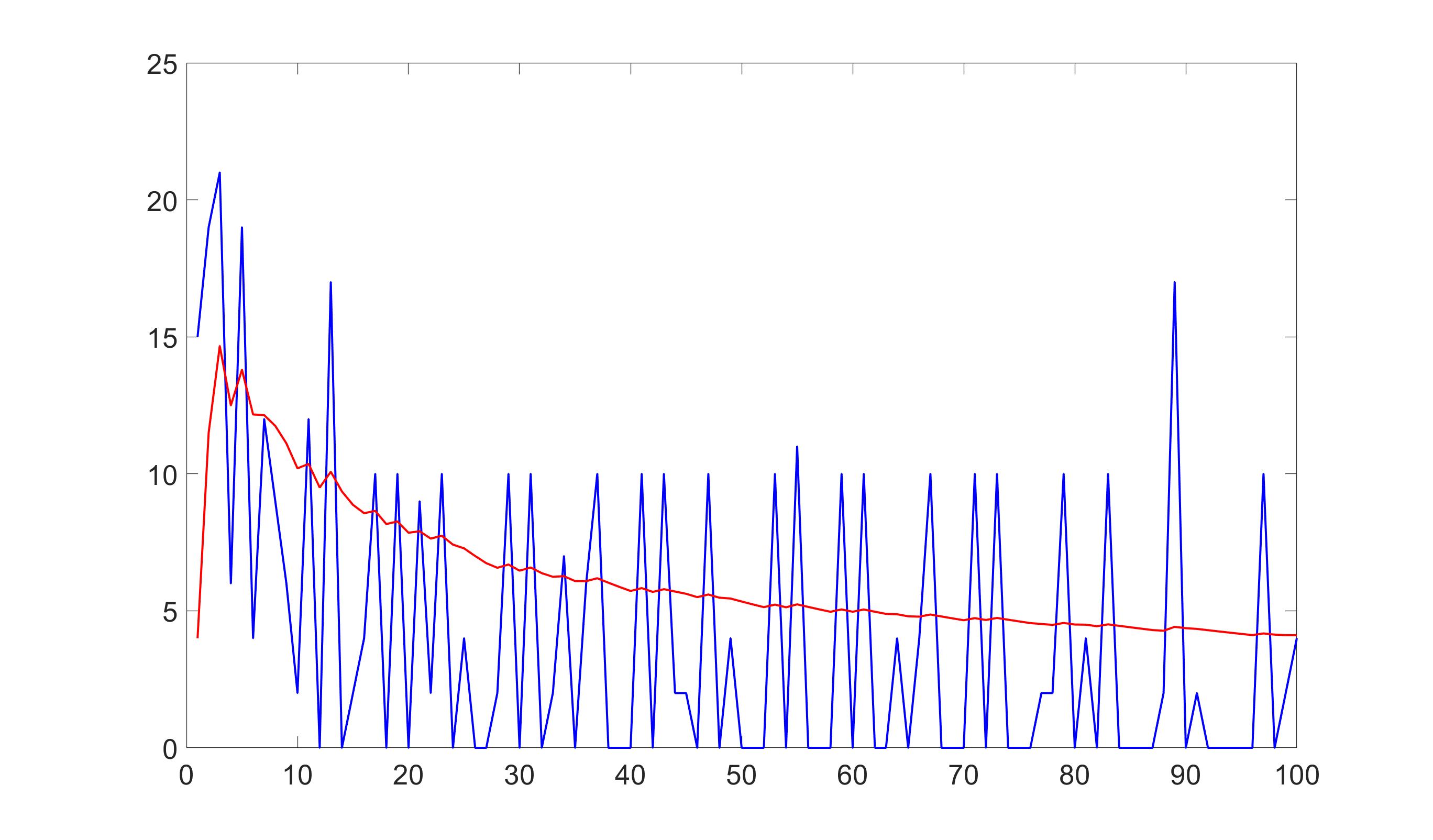
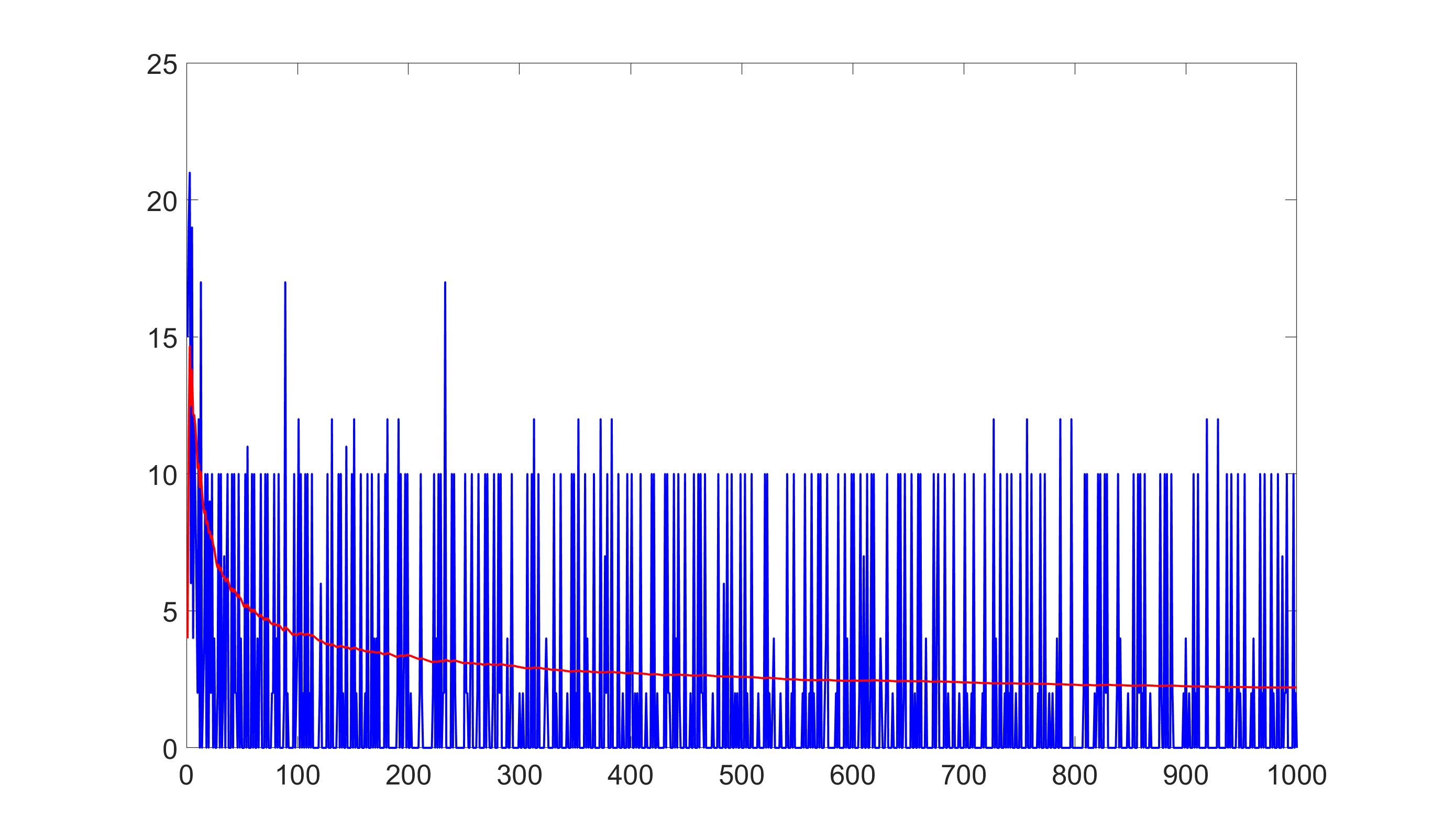
Voor beide grafieken geldt dat de blauwe lijn de grafiek van de interessantheidsfunctie is en de rode de gemiddelde interessantheid tot een bepaald punt. We zien hier twee grillige grafieken. Dit is ook wel de verwachten omdat bijvoorbeeld priemgetallen vrij willekeurig over de natuurlijke getallen verdeeld liggen. Wat we hier echter wel direct uit kunnen halen is dat zelfs tot $1000$ geldt dat $3$ het meest interessante getal is. Zoals gezegd geeft de rode lijn steeds de gemiddelde interessantheid aan tot een bepaalde waarde. Zo zien we in het begin een hoge gemiddelde interessantheid, terwijl dit verder op de grafiek sterk daalt en uiteindelijk afvlakt. We kunnen in dit specifieke geval, dus bij deze gekozen  interessantheidsverzameling en waardering, kijken wat die gemiddelde waarde is. Tot $100$ is die $4{,}2200$, tot $1000$ is die $2{,}2130$ en als we zelfs tot $1 000 000$ gaan, dan krijgen we een gemiddelde interessantheid van $0{,}7960$. In
dit geval zien we dat het gemiddelde steeds kleiner wordt en deze zal uiteindelijk zelfs $0$ worden. Die gemiddelden kunnen we handig gebruiken om grof te zeggen hoe interessant een getal is. Tot de $1000$ is een getal gemiddeld al interessant als deze interessantheid groter dan $2{,}2130$ heeft en voor hele grote getallen geldt in dit geval zelfs dat ze bij elke interessantheid ongelijk aan $0$ gemiddeld al interessant zijn.

Bij keuze van een andere interessantheidsverzameling en een andere waardering zou het kunnen dat $3$ helemaal niet meer het meest interessante getal is en dat we daar nog wat langer voor moeten zoeken en wellicht wordt het gemiddelde veel hoger of lager of verandert dit steeds.

	Speel zelf met interessantheid! Zelf bepalen hoe je interessantheid definieert? Op www.pyth.eu/pypy vind je een pagina met de code voor een programma waarin je interessantheid van getallen kan berekenen met jouw eigen gekozen waardering. Op die pagina wordt ook uitgelegd hoe het programma werkt en hoe je de code zelf kan aanpassen zodat je je favoriete eigenschappen kan toevoegen aan het programma.

 

	We horen graag over jullie eigen definities van interessantheid en over jullie bevindingen met het programma! Wat is het meest interessante getal in jouw berekening? Geef naast een definitie ook vooral jullie favoriete interessante eigenschap door. De mooiste definities of eigenschappen kunnen we dan bespreken in een mini vervolg. Daarnaast kunnen we nog eens een berekening maken met de ingezonden eigenschappen en kijken of 3 nog steeds zo interessant is.

Onder de knop [Bekijk oplossing] vind je de Python programmacode bij dit artikel. 

Bekijk oplossing