
Kleine nootjes 64-6
FaCturen
Jerome boekt facturen. In de $80\%$ gemakkelijke steekt hij $20\%$ van zijn tijd, voor de $20\%$ moeilijke heeft hij $80\%$ van zijn tijd nodig.
Hoeveel keer sneller gaan de gemakkelijke t.o.v. de moeilijke?
Zelfteller
De vijf getallen hieronder vormen elk een code. De cijfers op de even posities in elke code zijn de cijfers in de code. De cijfers op de oneven posities geven aan hoe vaak het cijfer erna in de code voorkomt. Voor maar één van de vijf codes klopt dit.
Wat is de correcte code?
- $14131211$
- $14223123$
- $14233221$
- $14322231$
- $15141311$
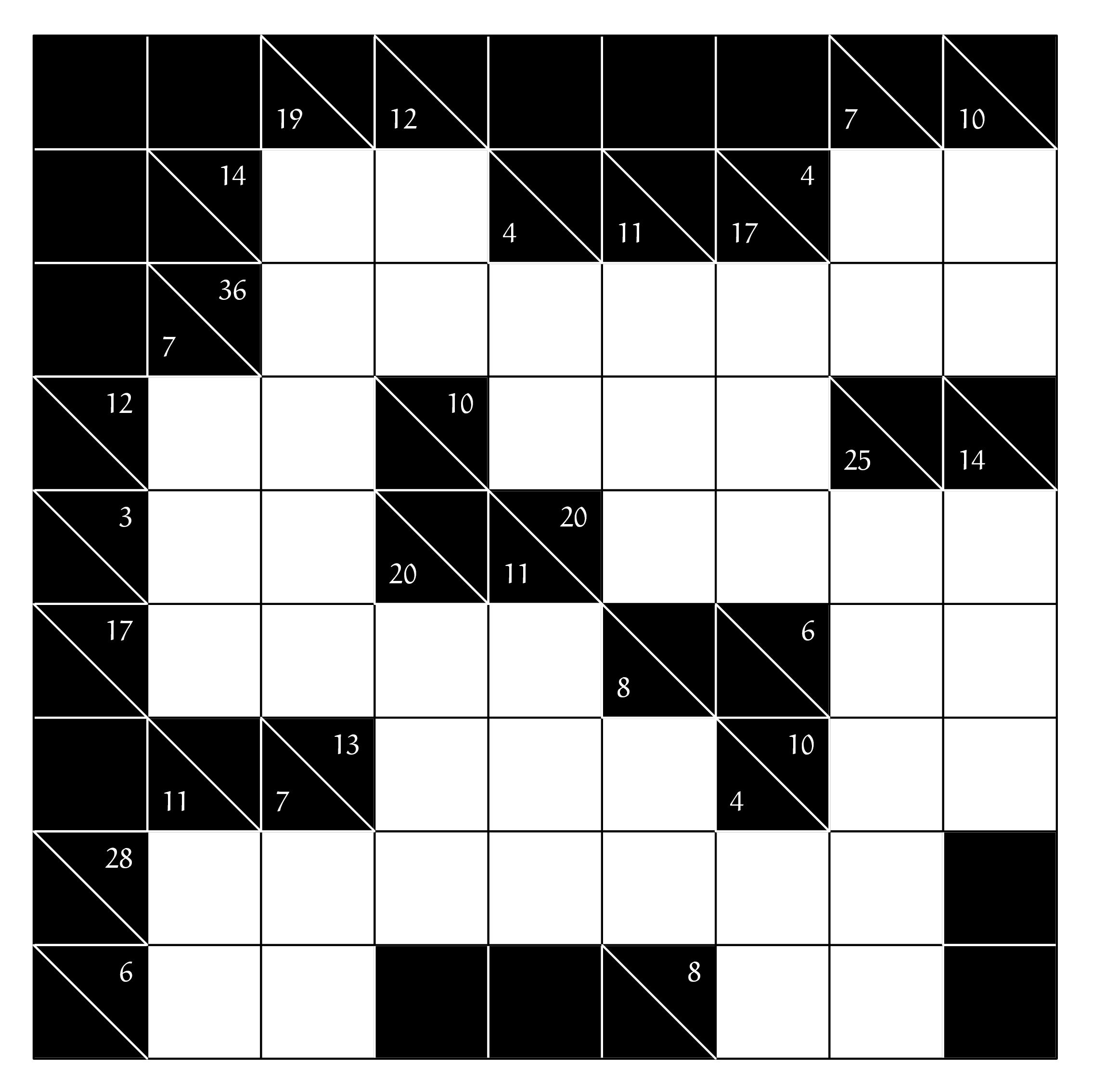
Kakuro
In de witte cellen komt steeds één cijfer. Sommige zwarte cellen bevatten een diagonaal met getallen erin, de sleutels. Het getal boven rechts geeft een horizontale sleutel en een getal onder links geeft een beneden sleutel dat de som is van horizontaal of verticaal. Doel is om cijfers van $1$ t/m $9$ in te vullen. Cijfers mogen maar een keer voorkomen per sleutel.
Tot de macht 3
Welke uitspraak is fout?
- $153 = 1^3 + 5^3 + 3^3$
- $370 = 3^3 + 7^3 + 0^3$
- $371 = 3^3 + 7^3 + 1^3$
- $407 = 4^3 + 0^3 + 7^3$
- $518 = 5^3 + 1^3 + 8^3$
Fibokwadraat
De rij van Fibonacci begint met $0$ en $1$ en vervolgens is elk volgend element van de rij steeds de som van de twee voorgaande elementen.
Wat is het enige kwadraat (naast $0$ en $1$) uit deze rij?
Bekijk oplossing
