Het kloostergewelf dat we als een tussenfase in de constructie van het kruisgewelf zagen is zelf ook vaak gebruikt in de architectuur. Niet alleen in kloosters, maar bijvoorbeeld ook als dak van het Maple Leaf ijshockey stadion in Toronto of voor kassen. Een mooi voorbeeld hiervan vind je in de botanische tuinen van Genève (figuur 1).

Een vierkante paraplu

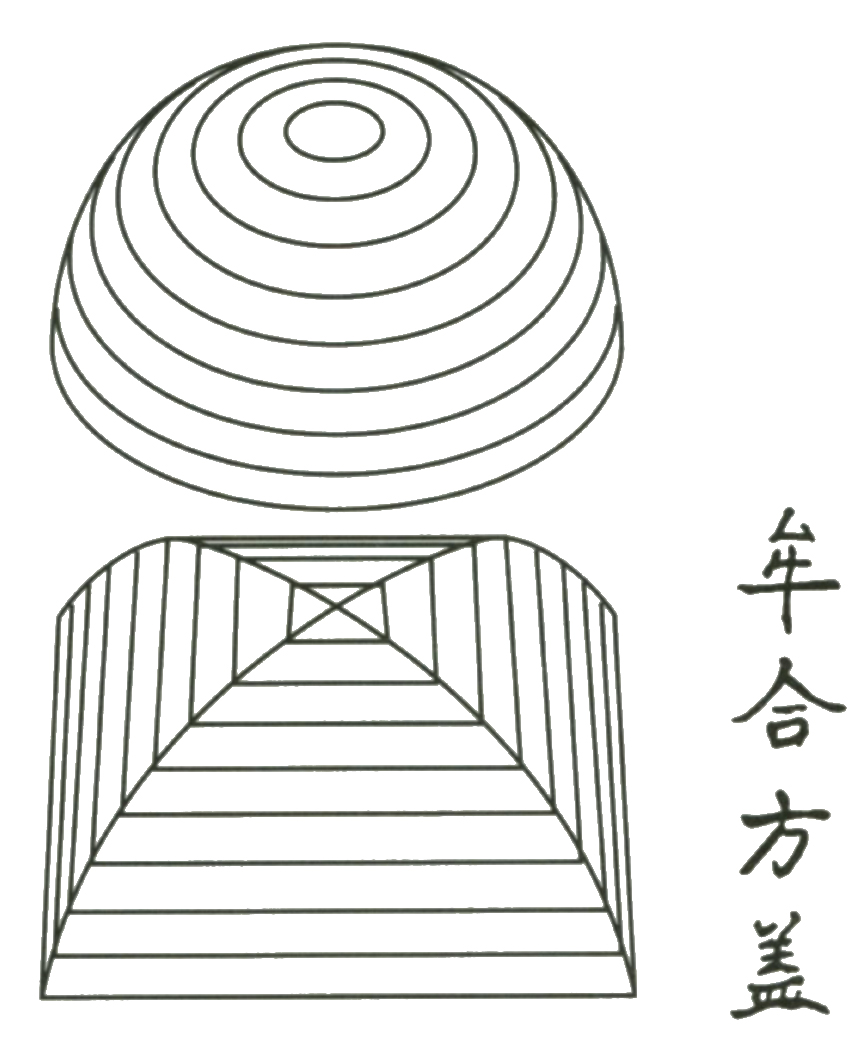
De doorsnede van twee elkaar loodrecht snijdende gelijke cilinders heet ook wel een equidomoïde. Internationaal staat de vorm bekend als het 'lichaam van Steinmetz'. De holte in het linkerplaatje en de bolle figuur in het rechterplaatje in figuur 2 zijn dus beide een halve equidomoïde. Al in de derde eeuw na Christus bedacht de Chinees Liu Hui deze figuur in de zoektocht naar een formule voor de inhoud van een bol. Hij noemde de figuur mou he fang gai, het lichaam gevormd door twee vierkante paraplu's, en hij zou het kloostergewelf dus een vierkante paraplu hebben genoemd. Hoe kwam hij op deze figuur? De Chinezen werkten met verhoudingen, in het bijzonder de verhouding tussen de oppervlakte van een vierkant en die van zijn ingeschreven cirkel. Liu Hui realiseerde zich dat je ook met die verhouding kunt werken als je een omhullende figuur voor een bol hebt die op iedere hoogte een vierkant als dwarsdoorsnede heeft in plaats van een cirkel. Zijn paraplulichaam heeft precies die eigenschap.

Figuur 2 - Constructies van een kloostergewelf uit de vorige Pythagoras

Negen Hoofdstukken

De verhouding tussen de oppervlakte van een vierkant en die van zijn ingeschreven cirkel was gelijk aan $4 : 3$ volgens het alomgebruikte handboek Jiuzhang suanshu, "Negen Hoofdstukken over de Wiskunst", uit de tweede eeuw voor Christus. Dit betekent dat volgens dit handboek onze waarde $\pi$ gelijk was aan $3$. Op basis van het vergelijken van de massa's van een bol van diameter $d$ en zijn omgeschreven kubus met zijden van lengte $d$ vonden de Chinezen een schatting voor de verhouding tussen de volumes van een kubus en een bol. Ze schatten dat $V_{\rm kubus} : V_{\rm bol} = 16 : 9$ en dat dus gold dat $V_{\rm bol} = \frac{9}{16}d^3$ voor een bol met diameter $d$.

In het begin van de tweede eeuw na Chr. had de astronoom-wiskundige Zhang Heng bedenkingen bij sommige van de formules die iedereen klakkeloos uit de Negen Hoofdstukken overnam. Voor de verhouding tussen de oppervlakte van een vierkant en die van zijn ingeschreven cirkel, $4 : p$, kwam hij tot een nieuwe schatting, met $p (= \pi) = \sqrt{10} \approx 3{,}16$. Hij bedacht tevens dat de verhouding van het volume van een kubus tot zijn ingeschreven cilinder ook $4 : p$ moest zijn. Vervolgens zou de verhouding tussen de volumes van een rechte cilinder met diameter $d$ en hoogte $d$ en die van zijn ingeschreven bol volgens hem ook $4 : p$ zijn. Hoewel hij geen formule opschreef voor $V_{\rm bol}$, leidt een combinatie van deze twee verhoudingen tot de perfecte aanpassing van de oude formule $V_{\rm bol} = \frac{9}{16}d^3$. Dit is precies wat Liu Hui in de derde eeuw bedacht:

Als $V_{\rm kubus} : V_{\rm cilinder} = 4 : \pi$, dan is $V_{\rm kubus} : V_{\rm bol} = 16 : \pi^2$.

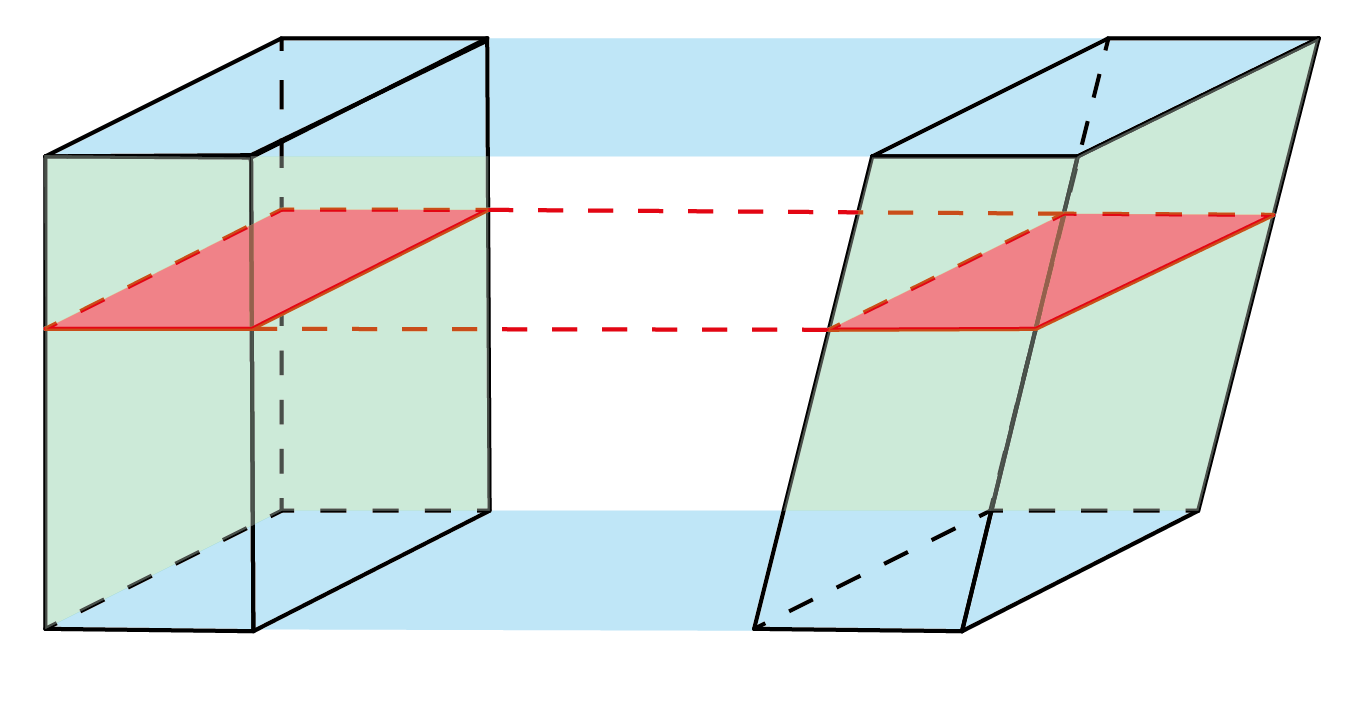
Hij had inmiddels ook de benadering voor $\pi$ verbeterd van $3$ tot $3{,}141024$ door net als Archimedes gebruik te maken van ingeschreven en omgeschreven veelhoeken en zocht naar een bevestiging van de formule voor de inhoud van de bol. Hij wilde daarvoor gebruik maken van een idee dat nu bekend staat als het principe van Cavalieri (zie figuur 3):

"Als tussen twee horizontale vlakken twee lichamen worden geconstrueerd, zodanig dat op elke hoogte de horizontale doorsnedes van de twee lichamen dezelfde oppervlakte hebben, dan hebben beide lichamen hetzelfde volume." 

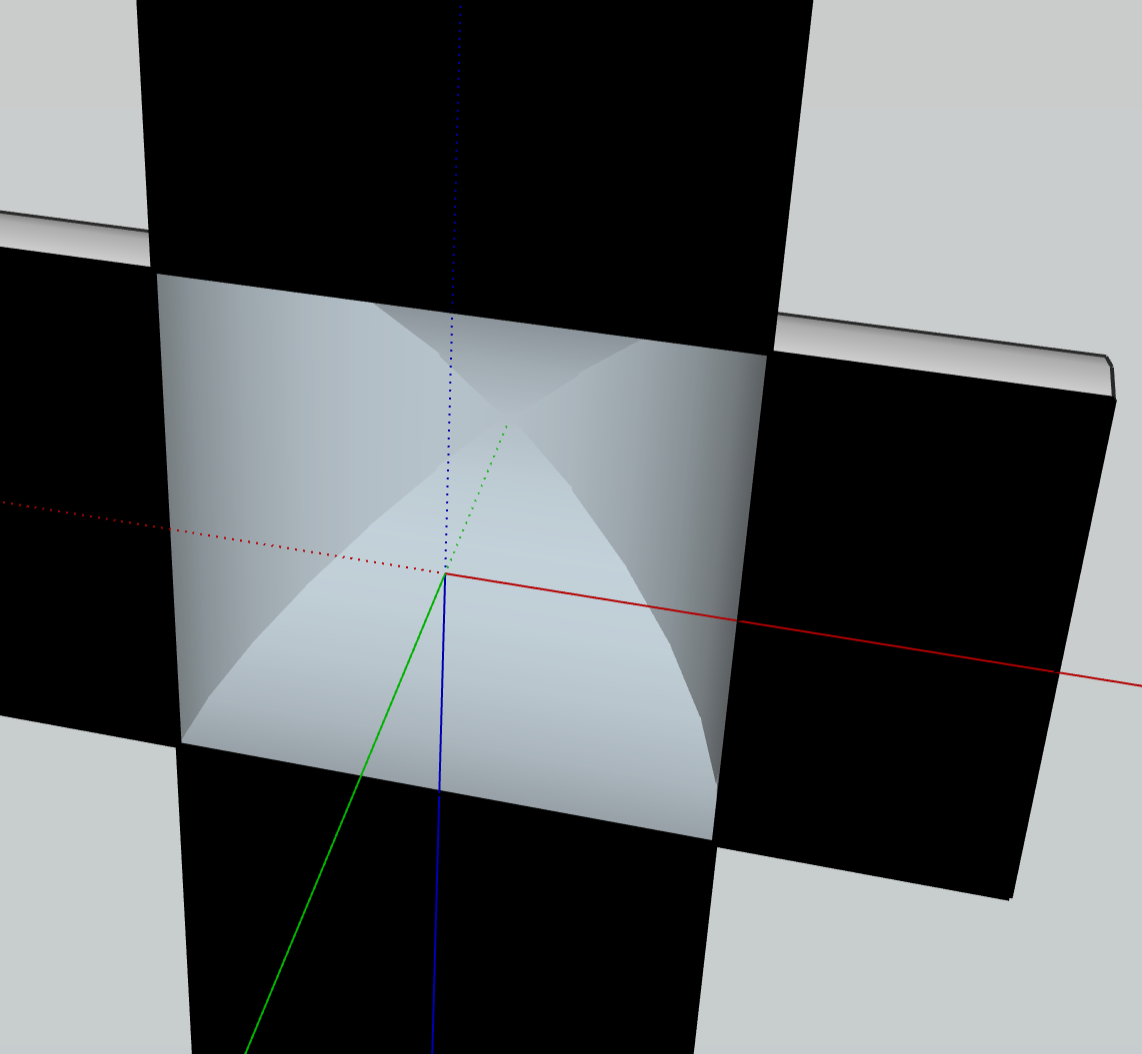
De omhullende 'paraplu' heeft op iedere hoogte een vierkante doorsnede die precies rond de cirkelvormige doorsnede van de bol past, zoals te zien in figuur 4. De oppervlakten van de doorsnedes verhouden zich dus op iedere hoogte als 4 : r, en Liu zag in dat daarmee de volumes van beide figuren zich ook verhouden als 4 : r. Nu hoefde hij alleen nog maar het volume van de equidomoïde te vinden om het bolvolume te kennen. Dat lukte hem helaas niet.

Slim gebruik van oppervlakten van dwarsdoorsneden

Zo'n twee eeuwen later vond Zu Chongzhi een nog betere benadering voor $\pi$, namelijk $\frac{355}{113} \approx 3{,}1415929$. Met zijn zoon Geng probeerde hij het werk van Liu af te ronden. Ze bestudeerden daarvoor een achtste van de equidomoïde.

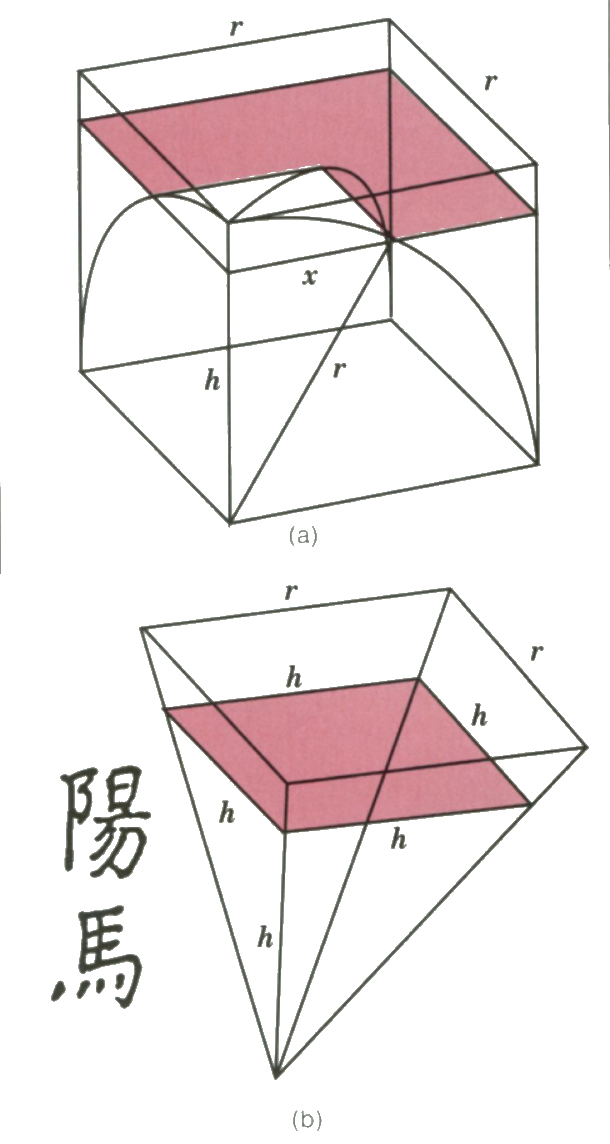
Door niet te kijken naar de vierkanten die het paraplulichaam vormen, maar naar de oppervlakte van het complement binnen een omgeschreven kubus met zijden $r$, lukte het hen om tot een nuttige verhouding te komen. Kijk hiervoor naar figuur 5: als op hoogte $h$ boven het grondvlak de vierkante doorsnede van de figuur zijde $x$ heeft, dan heeft het L-vormige complement een oppervlakte van $r^2 - x^2$. Maar door de vorm van de paraplu geldt $h^2 = r^2 - x^2$. Dus het volume van een achtste paraplulichaam is gelijk aan dat van een lichaam dat op iedere hoogte h boven zijn grondvlak een doorsnede van oppervlakte $h^2$ heeft. Zie figuur 5. De Chinezen kenden zo'n figuur, want Liu had gevonden dat het volume van een piramide met vierkante basis $b^2$ en hoogte $h$ gelijk was aan $\tfrac{1}{3}hb^2$. Met $h = b = r$ heeft de gehele piramide in figuur 5 dus volume $\tfrac{1}{3}r^3$, zodat de achtste equidomoïde een volume van $r^3 - \tfrac{1}{3}r^3 = \tfrac{2}{3}r^3$ heeft. En de gehele equidomoïde een volume van $\tfrac{16}{3}r^3$. Dankzij Liu's idee wisten vader en zoon Chongzhi dat de bol zich verhoudt tot het paraplulichaam als $\pi : 4$ en daarmee vonden ze dus dat de bol een inhoud van $\tfrac{4}{3}\pi^r$ heeft. De formule uit de Negen Hoofdstukken was hiermee eindelijk ontkracht.

En het kloostergewelf heeft dus een belangrijke rol gespeeld bij een afleiding van de formule voor het volume van een bol!