Voor wie sudoku niet kent: de puzzel bestaat uit een vierkant van 9 bij 9 vakjes. Een aantal cijfers zijn gegeven in de beginsituatie. Op elke rij en in elke kolom moet de puzzelaar de cijfers 1 t/m 9 plaatsen. Daarnaast is het vierkant opgedeeld in 3 × 3 kleinere vierkanten, die ook elk de cijfers 1 t/m 9 moeten bevatten.

De basiCs

Laten we eerst wat eenvoudige technieken bespreken, en natuurlijk even een notatie afspreken. Met (R7,K6) bedoelen we het vakje in de 7e rij en de 6e kolom. Verder nummeren we ook de $3 \times 3$ vierkantjes van links naar rechts en dan van boven naar beneden met V1 t/m V9. V1 is dus het vak linksboven en V4 is het linker vak op de middelste rij.

Wanneer je aan een sudoku begint, dan zie je vaak meteen wel een aantal cijfers die je kunt invullen. Sommige cijfers zijn heel erg simpel te vinden, wat later zul je wellicht iets meer moeten nadenken, zoals bij de volgende puzzel. 

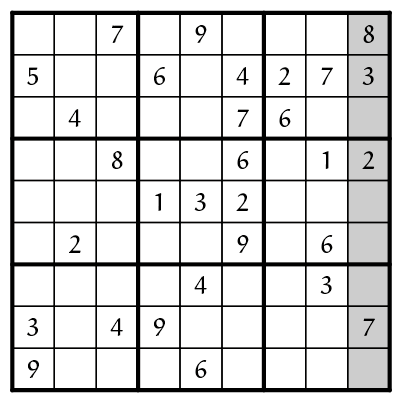
In de laatste kolom missen we nog de $1, 4, 5, 6$ en $9$, maar we zien dat de $6$ niet op (R3,K9) kan, ook niet op (R5,K9) en (R6,K9), en ook niet op (R9,K9). Blijft over de positie (R7,K9), en daar vullen we dan de $6$ in. Dit is een speciaal geval van de volgende twee basis technieken:

1. Kijk welke cijfers er nog ontbreken in een rij, kolom of vierkant, en ga voor alle lege vakjes na of het misschien zo is dat slechts één van de ontbrekende cijfers in aanmerking komt;
2. Bepaal voor een ontbrekend cijfer in een rij, kolom of vierkant of het zo is dat dit cijfer slechts op één bepaalde plaats kan staan.

Een volgende techniek is die van de "volle rijen of kolommen". Kijk maar eens naar de volgende puzzel:

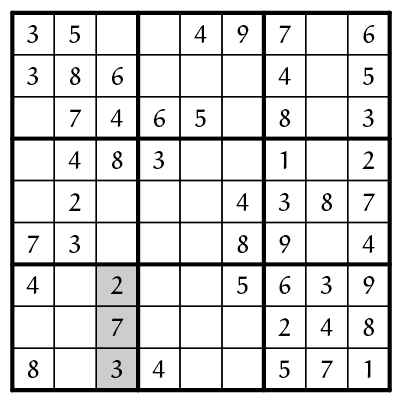
In de 2^e kolom staat op (R1,K2) een $5$, hetgeen betekent dat in de vierkanten V4 en V7 de cijfers $5$ in de 1^e of 3^e kolom dienen te komen. Maar in vierkant V7 is de laatste kolom (grijs) al geheel gevuld, dus kan de $5$ daar enkel in het 1^e kolommetje staan. Daar is nog slechts één positie vrij, dus vullen we de $5$ in op de plaats (R8,K1). (Overigens hadden we deze $5$ ook kunnen vinden met onze eerste basistechniek, namelijk door gebruik te maken van de $5$'en in de 7^e en 9^e rij, en de $5$ in de 2^e kolom. Maar dit doet er niet toe, er zijn wel vaker meerdere manieren om een ontbrekend cijfer in te vullen.)

Opgave 1 Probeer nu deze puzzel zelf af te maken.

 Voor sommige, vaak als "moeilijk" geclassificeerde, puzzels hebben we nog een extra techniek nodig. Dit is een techniek waarbij we onthouden dat voor een bepaald cijfer slechts één rij of één kolom van een bepaald vierkant in aanmerking komt. Deze wetenschap wordt dan vervolgens uitgebuit om dat bepaalde cijfer in te kunnen vullen in een andere rij of kolom. De techniek kunnen we het beste illustreren middels een voorbeeld. Bekijk daartoe de volgende sudoku, die we al voor een behoorlijk deel hebben ingevuld met de methoden die we eerder bespraken.

Eerst constateren we dat de $6$ in de 7^e kolom gedwongen in de eerste kolom van V3 terecht dient te komen. Immers, het deel van de 7^e kolom in V6 is al helemaal gevuld, terwijl op (R7,K7) en (R9,K7) geen $6$ kan staan wegens de $6$'en in de 7^e en 9^e rij. Laten we dus onthouden dat er in de 1^e kolom van V3 sowieso een $6$ staat. We kunnen dit in het diagram hierboven aangegeven door een ellips te tekenen die om de 1^e kolom staat (en eventueel een $6$ bij de rand van de ellips te noteren); in de praktijk kun je deze informatie vaak gewoon onthouden.

Kijk vervolgens naar de 3^e rij, waar de cijfers $4, 6, 7, 8$ en $9$ ontbreken. In het laatste hokje van die rij kan sowieso geen $7$, $8$ en $9$ staan omdat deze al voorkomen in de 9^e kolom. Maar een $6$ kan ook niet, want dit cijfer komt al voor in de 1^e kolom van V3, zoals we zojuist hadden geconcludeerd. Kortom, voor (R3,K9) blijft enkel de mogelijkheid $4$ over, en dit vullen we dan ook in. Het "vreemde" aan deze methode is dus dat, door te onthouden waar een $6$ moet staan zonder precies te weten waar, we een $4$ kunnen invullen!

Oplossen met Cijferparen

Het grote geheim achter het kunnen oplossen van alle sudoku's bestaat uit het gebruik van zogenaamde cijferparen. Als we weten dat er voor een bepaald vakje nog slechts twee mogelijkheden zijn, dan noteren we die twee cijfers in de linkerbovenhoek. Kijk bijvoorbeeld maar naar de volgende puzzel:

Het is duidelijk dat de $3$ en de $7$ nog ontbreken in de 2^e rij, en dus noteren we "$37$" in (R2,K7) en (R2, K9). En ook in V2 is het duidelijk, dus noteren we "$37$" in (R3,K4) en (R3,K6). Omdat het cijferpaar ''$37$'' twee maal voorkomt in de 3^e rij, weten we dat de $3$ en de $7$ in die twee vakjes moeten komen, en dat er in de 3^e rij dan enkel nog de cijfers $2$ en $9$ ontbreken. Dus kunnen we meteen ook "$29$" noteren in (R3,K7) en (R3,K9). Laten we nog eens een voorbeeld nemen, en de techniek illustreren. Bekijk hiertoe de volgende puzzel, die we al deels hebben opgelost. De grijze vakjes geven aan dat we voor die cijfers de basistechnieken hebben gebruikt.

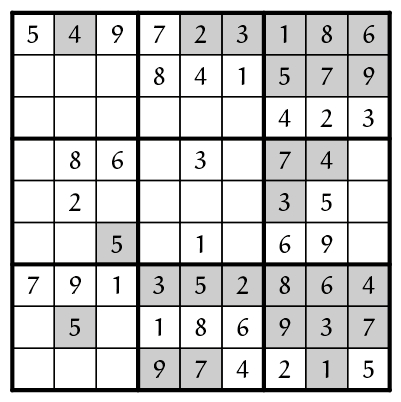
Als we hier naar de 2^e kolom kijken, dan zien we dat $1, 3, 6, 7$ ontbreken. Vanwege de $1$ en $7$ in de 2^e rij betekent dit voor positie (R2,K2) dat daar het cijferpaar $3$, $6$ genoteerd kan worden. Voor (R3,K2) hebben we nog 3 mogelijkheden over, te weten $1, 6, 7$, dus in die cel kan geen cijferpaar genoteerd worden. Voor (R6,K2) kunnen we wel weer een paar noteren, namelijk $3, 7$, en tenslotte vinden we voor (R9,K2) het paar $3, 6$.

Maar dit is interessant: in de 2^e kolom komt dan tweemaal het paar $3, 6$ voor, hetgeen moet betekenen dat de $3$ en de $6$ op de plaatsen (R2,K2) en (R9,K2) staan, we weten enkel nog niet welk van de twee waar zal staan. Maar dan kunnen we $3$ als mogelijkheid schrappen in het zojuist in (R6,K2) gevonden cijferpaar, en de 7 als definitief noteren. En passant betekent het dat het enige overgebleven cijfer in de 2^e kolom, een $1$, op plaats (R3,K2) komt.

De rest van de puzzel blijkt nu helemaal oplosbaar met onze basistechnieken! En dat, terwijl we deze puzzel uit een boek genaamd Sudoku Genius hebt gehaald, waarbij we de puzzel als "moeilijkheidsgraad 4" werd gekarakteriseerd. Wij weten inmiddels wel beter, en draaien er onze hand niet meer voor om!

Het gebruik van cijferparen is al gebleken een krachtige methode te zijn. Maar de methode is nog krachtiger dan je wellicht voor mogelijk houdt. Dit vergt echter wel enige observatie-kracht. Kijk eens naar de volgende puzzel, waarbij zoals gewoonlijk zelf alweer wat cijfers hebben ingevuld middels de basistechnieken. Tijdens dat proces zijn we onderweg al wat cijferparen tegengekomen, die we in een aantal vakjes al hebben genoteerd.

Kijk nu eens aandachtig naar het rijtje cijferparen in de laatste rij van vierkant V5. Daar staan drie cijferparen, waarin enkel de cijfers $5, 8, 9$ voorkomen. Maar dit betekent dat die laatste rij precies al die cijfers zal bevatten. Immers, als in (R6,K4) een $5$ staat, dan komt er automatisch in (R6,K6) een $8$, en dus in (R6,K5) een $9$, waardoor het rijtje $598$ ontstaat. Als er in (R6,K4) een $9$ staat, dan wordt het rijtje $985$. Dus weten we zeker dat de $5$ in het laatste rijtje van V5 terecht zal komen, en dus kan er op (R4,K4) alleen nog maar een $1$ staan. Met andere woorden, zonder dat we precies weten hoe het laatste rijtje van vierkant V5 er uit ziet, kunnen we toch concluderen dat er op (R4,K4) een $1$ dient te staan!

We zien dus dat we alert dienen te zijn op zowel identieke cijferparen zoals in (R6,K2), (R6,K3) of in (R7,K2), (R7,K8), als op bij elkaar passende drietallen van cijferparen. Je zou je zelfs kunnen voorstellen dat er 4 bij elkaar passende cijferparen voorkomen in een puzzel, bijvoorbeeld $12$, $23$, $34$ en $14$. Zo'n situatie zal men echter zelden aantreffen, en vaak kan men zich beperken tot een paar identieke cijferparen, of een drietal bij elkaar passende cijferparen. Er kunnen zich nog andere situaties met bij elkaar passende cijferparen voordoen, die er voor kunnen zorgen dat een vastzittende puzzelaar weer verder kan. Kijk maar eens naar de volgende sudoku:

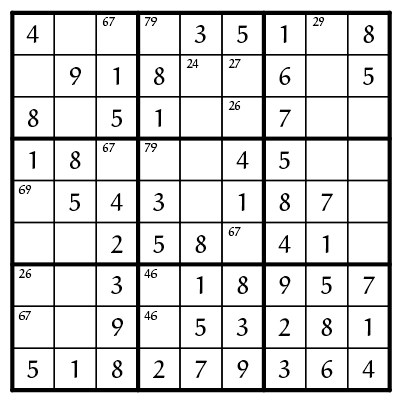
In de 6^e kolom zien we drie cijferparen staan, die samen de verdeling van de cijfers $2, 6, 7$ bepalen. Voor het cijfer $2$ in die kolom geldt echter dat het enkel kan voorkomen in (R2,K6) of (R3,K6). Anders gezegd: er zal sowieso een $2$ staan in de laatste kolom van vierkant V2. Dit betekent meteen dat de $2$ in het resterende deel van vierkant V2 weggestreept kan worden als mogelijkheid. Bijvoorbeeld in (R2,K5), zodat daar enkel een 4 als mogelijkheid overblijft, en dat vullen we dan ook in.

Nog een voorbeeld, kijk maar eens naar de volgende puzzel:

Kijk nu eens naar vierkant V6. Daar ontbreken de cijfers $1, 4, 5, 8$ en $9$. Maar de cijfers $1, 4$ en $8$ moeten terecht komen in de 1^e kolom van V6, want dat zijn de cijfers die nog ontbreken in de 7^e kolom. Dus concluderen we dat de $5$ en $9$ enkel op de plaatsen (R5,K8) en (R5,K9) kunnen staan. In beide hokjes noteren we dus het cijferpaar $5, 9$. Je wordt uitgenodigd nu zelf de puzzel verder op te lossen!

De intelligente gok

Er zijn behoorlijk wat sudoku-puzzels, die middels de basistechnieken en cijferparen opgelost kunnen worden. Door cijferparen te noteren in de sudoku kun je op een gegeven moment bij elkaar behorende cijferparen vinden en daaruit conclusies trekken, zoals we hierboven al lieten zien. Sommige boeken raden aan om alle mogelijkheden in een vakje te noteren, maar dat wordt enerzijds nogal een knoeiboel, anderzijds is het dus helemaal niet nodig, met cijferparen kun je alle sudoku's oplossen. Maar er zijn puzzels, waar je op een gegeven moment vast komt te zitten met de technieken die hiervoor zijn besproken. In dat geval dien je een gecalculeerde "gok" te maken, door op een intelligente manier één van de cijferparen te kiezen en daarna de twee mogelijke paden te doorlopen. Stel bijvoorbeeld dat je het cijferpaar "$27$" uitkiest. Dan kijk je wat er gebeurt als je de $2$ kiest in dat vakje, en wat er gebeurt als je de $7$ kiest. In mijn boek Los elke sudoku op wordt een heel mooie methode gepresenteerd waarmee je dit proces kunt uitvoeren, en dat leidt tot heel verrassende uitkomsten. Soms loopt een van de paden dood, dat wil zeggen er ontstaat een tegenstrijdigheid in de oplossing bij een van de twee keuzes. Een andere mogelijkheid, eigenlijk ook heel interessant vanuit wiskundig oogpunt, is waarbij beide keuzes in een bepaald vakje tot hetzelfde cijfer leiden! Dan kun je dat cijfer met pen noteren, want het is zeker dat dit het juiste cijfer is in dat vakje.

Computerhulp

Er zijn boeken waarin allerlei patronen te vinden zijn die kunnen helpen als je vast zit, bijvoorbeeld de "X-wing", "Y-wing", "zwaardvis" en nog moeilijker patronen. Voor een mens zijn deze patronen nagenoeg niet te vinden in een puzzel. Maar het is ook totaal niet nodig. Het blijkt dat de methode van de cijferparen, inclusief de techniek van de intelligente gok, deze patronen automatisch vindt en dus leidt tot de uiteindelijke oplossing van de puzzel. Zelfs de allermoeilijkste sudoku van de wereld kun je oplossen met de bovenstaande technieken. (Het kost je een regenachtige middag om tot een oplossing te komen voor die sudoku!)

Ik wens je veel succes bij het oplossen van steeds moelijker sudoku's!

Het is leuk om oplostechnieken zoals hierboven beschreven zelf te programmeren, en een programma te maken dat hints geeft als je vastzit. Het programma op www.sudokuhints.com helpt erg goed bij het vinden van cijfers middels logische stappen. Bovendien vertelt dit programma je ook wanneer de logische stappen uitgeput zijn en je je toevlucht dient te gaan zoeken tot intelligent gokken. Maar dit programma geeft het op als de puzzel vast zit en je een cijferpaar moet kiezen om verder te kunnen en de twee paden af te lopen. Het zou leuk zijn als er lezers zijn die software kunnen maken die ook deze geavanceerde techniek aan boord heeft. Daarover in een later artikel meer!

		Meer lezen
Wil Schilders schreef de boeken Los elke sudoku op, Medium sudoku's oplossen en Moeilijke sudoku's oplossen waarin een 9-staps methode wordt gepresenteerd waarmee zelfs de allermoeilijkste sudoku’s kunnen worden opgelost.