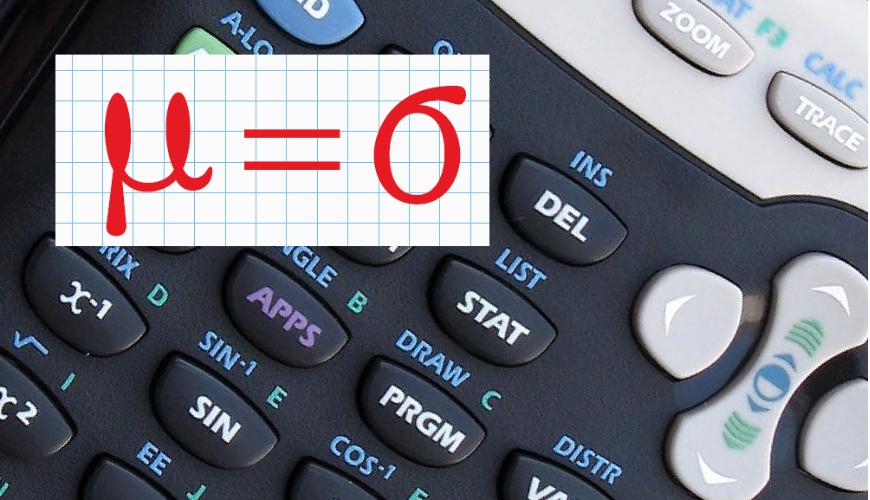
mu = sigma
In de beschrijvende statistiek bestaan twee belangrijke maten: $\mu$, het gemiddelde ('centrum' van een groep getallen) en $\sigma$, de standaardafwijking ('spreiding' rondom dat gemiddelde). Meestal zijn deze twee maten niet gelijk. Wat als ze wel gelijk zijn?
Met de grafische rekenmachine zijn ze makkelijk te berekenen, in Excel gebruik je de formules "=GEMIDDELDE" en "=STDEV.P". De definities zijn als volgt:
$$\mu = \frac{\sum{x_i}}{n} \\ \sigma = \sqrt{ \frac{ \sum(x_i-\bar{x})^2}{n} }.$$
Meestal zijn n en v niet gelijk. Zo kan het aantal gewerkte uren van fulltime werknemers in een bedrijf in een bepaalde week bijvoorbeeld $40{,}2$ uur zijn, met een standaardafwijking van $6{,}3$ uur. De waarden $\mu$ en $\sigma$ van de zes u uitkomsten van een dobbelsteen is $3{,}5$, met een standaardafwijking van ongeveer $1{,}708$ (exact: $\sqrt{105/6}$). Of: het gemiddelde cijfer voor een proefwerk in een klas is $6{,}1$, met een standaardafwijking van $1{,}8$. Gemiddelde en standaardafwijking zijn zelden hetzelfde.
Daarom is het leuk om te kijken naar situaties waarin deze twee statistische maten wel gelijk zijn. Enige tijd terug kreeg ik een steekproef van $30$ rendementen van een aandeel, gemeten in de tijd. Het gemiddelde rendement daarin was $3{,}1\%$,
en de standaardafwijking van die rendementen (de 'beweeglijkheid', ook wel 'volatiliteit' geheten) was eveneens $3{,}1\%$. (Er is theoretisch een verschil tussen de standaardafwijking in een steekproef en die in een populatie. Ik beschouw hier steeds de 'verzameling' getallen als een populatie.) Gemiddelde en standaardafwijking waren dus precies gelijk! Toeval, zou je zeggen.
Natuurlijk, maar het zette me wel op het spoor van de volgende vraag:
Voor welke verzamelingen geldt: $\mu = \sigma$?
Een verzameling bestaande uit één getal heeft geen standaardafwijking. Dan kan dus nooit $\mu = \sigma$ gelden. We nemen voor de volgende gevallen steeds aan dat niet alle getallen gelijk zijn aan $0$.
Opdracht 1
Laat zien dat de eis dat $\mu = \sigma$ in een verzameling met twee getallen één van die beide getallen vastlegt.
Voor verzamelingen met drie getallen is een oplossing bijvoorbeeld $(0, 1, 2 + \sqrt3)$. Maar er zijn er nog veel meer. Het leek me daarom leuk om van hier alleen maar te kijken naar onderlinge ongelijke, niet-negatieve gehele getallen (inclusief $0$ dus). Een oplossing van dit probleem noem ik een '$\mu = \sigma$-oplossing'.
Opdracht 2
Bewijs dat er geen $\mu = \sigma$-oplossing met drie (onderlinge ongelijke, niet-negatieve gehele) getallen ('$n = 3$') bestaat. (Er zijn wel veel leuke 'bijna'-oplossingen zoals $(3, 225, 856)$, of $(92, 321, 1656)$.)
Opdracht 3
Een '$\mu = \sigma$-oplossing voor $n = 4$' is $(0, 1, 4, 9)$. Er is voor $n = 4$ nog een oplossing met $1, 4$ en $9$ er in. Welke?
Opdracht 4
Wat is het bijzondere aan de oplossing $(0, 1, 4, 9)$ voor $n = 4$? Kun je dit veralgemeniseren?
Opdracht 5
Een $\mu = \sigma$-oplossing voor $n = 5$ is $(1, 2, 3, x, y)$, met $\mu = \sigma = 10$. Vind $x$ en $y$.
Opdracht 6
Een $\mu = \sigma$-oplossing voor $n = 6$ is $(0, 1, 3, 7, 22, x)$. Wat is $x$?
Opdracht 7
Zoek $\mu = \sigma$-oplossing voor $n = 7, 8, 9$ en $10$.
Tip (0, 1, 2, 3, 4, 5, …) of (1, 2, 3, 4, 5, …) doen het bijna altijd goed…
