Als je optelt of vermenigvuldigt, maakt het niet uit hoe de haakjes staan, er geldt immers $(a + b) + c = a + (b + c)$ en ook $(a \times b) \times c = a \times (b \times c)$. Ook de volgorde maakt niet uit: $a + b = b + a$ en $a \times b = b \times a$.

Bij machtsverheffen maakt wel uit hoe de haakjes staan en wat de volgorde van de getallen is. Om dat goed te laten zien schrijven we, net als in veel programmeertalen, $a^{\hat{}}b$ in plaats van $a^b$. Dat de volgorde uitmaakt zie je aan $2^3 = 8$ en $3^2 = 9$. Bij drie of meer getallen zijn de haakjes echt belangrijk, kijk maar: $(2^{\hat{}}3)^{\hat{}}4 = 8^{\hat{}}4 = 4096$ en $2^{\hat{}}(3^{\hat{}}4) = 2^{\hat{}}81 = 2\,417\,851\,639\,229\,258\,349\,412\,352.$

Er is dus verschil tussen $(a^{\hat{}}b)^{\hat{}}c$ en $a^{\hat{}}(b^{\hat{}}c)$ De eerste is eigenlijk maar één machtsverheffing, de rekenregel $(ab)^c = a^{bc}$ wordt in de nieuwe notatie $(a^{\hat{}}b)^{\hat{}}c = a^{\hat{}}(b \times c)$. De tweede bestaat echt uit twee machtsverheffingen en je moet dus van rechts naar links werken (van boven naar beneden eigenlijk). Als we torentjes van machten gaan maken (machtstorens), gebruiken we dus de tweede versie; we willen op elke stap echt machtsverheffen. Uitgaande van een positief getal $a$ maken we de volgende rij: $a, a^a, a^{(a^a)}, a^{(a^{(a^a)})},\dots$; dit proces wordt ook wel ‘tetratie’ genoemd. We schrijven de rij dus als $a, a^{\hat{}}a, a^{\hat{}}a^{\hat{}}a, a^{\hat{}}a^{\hat{}}a^{\hat{}}a, \dots$ en denk eraan: we werken van rechts naar links.

In je rekenmachientje, of in een programma voor je computer kun je die rij het best als volgt programmeren: $a_0 := a$, en $a_{n+1} := a^{a_n}$.

Experimenten

Laten we wat startwaarden proberen: we beginnen met $a = 2$.

Dan krijgen we

$2^{\hat{}}2 = 4$,
$2^{\hat{}}2^{\hat{}}2 = 2^{\hat{}}4 = 16$,
$2^{\hat{}}2^{\hat{}}2^{\hat{}}2 = 2^{\hat{}}16 = 65\,536$,
$2^{\hat{}}2^{\hat{}}2^{\hat{}}2^{\hat{}}2 = 2^{\hat{}}65\,536 = \dots$ (een getal van $19\,729$ cijfers).

Dat explodeert dus behoorlijk. Bij $a = 1$ gebeurt niets interessants: $1^{\hat{}}1^{\hat{}}1^{\hat{}}1 = 1$, hoe vaak je ook macht verheft. Tussen $a = 1$ en $a = 2$ zit waarschijnlijk een omslagpunt, waar het proces van ‘tam’ overgaat in ‘explosief’.

Laten we in het midden kijken: $a = 1{,}5$. Dan krijgen we een rij die tam lijkt te beginnen: $a_1 = 1{,}837117307, a_2 = 2{,}106203352, a_3 = 2{,}349005318, \dots , a_9 = 5{,}911914861, \dots$ , maar $a_{12}$ is een getal van zestien cijfers (probeer maar). Dus $1{,}5$ zit nog in het explosieve gebied.

Als je naar links in het midden gaat zitten ziet het er tammer uit: $a_0 = 1{,}25, a_1 = 1{,}321714079, a_5 = 1{,}351952001, a_{10} = 1{,}352202885, a_{20} = 1{,}352203513, \dots$.

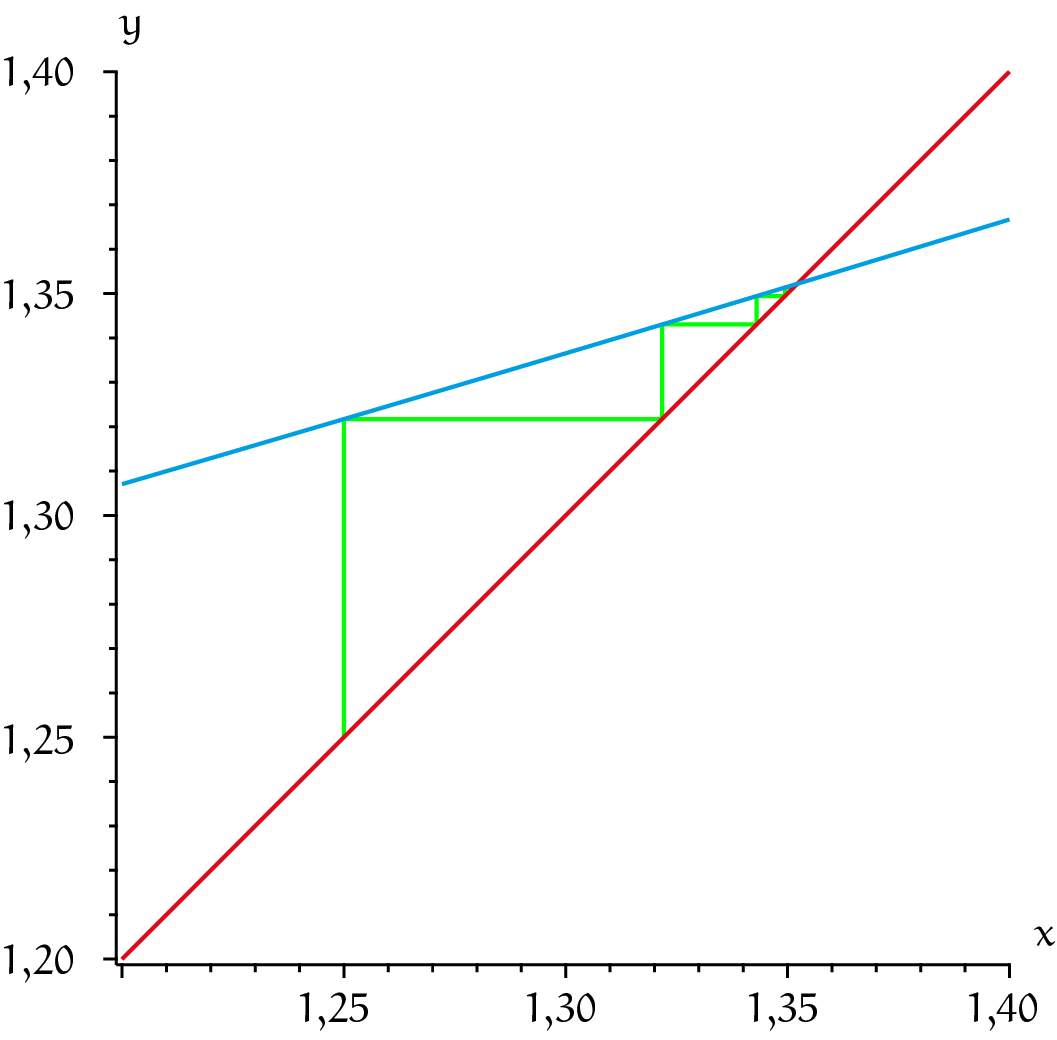
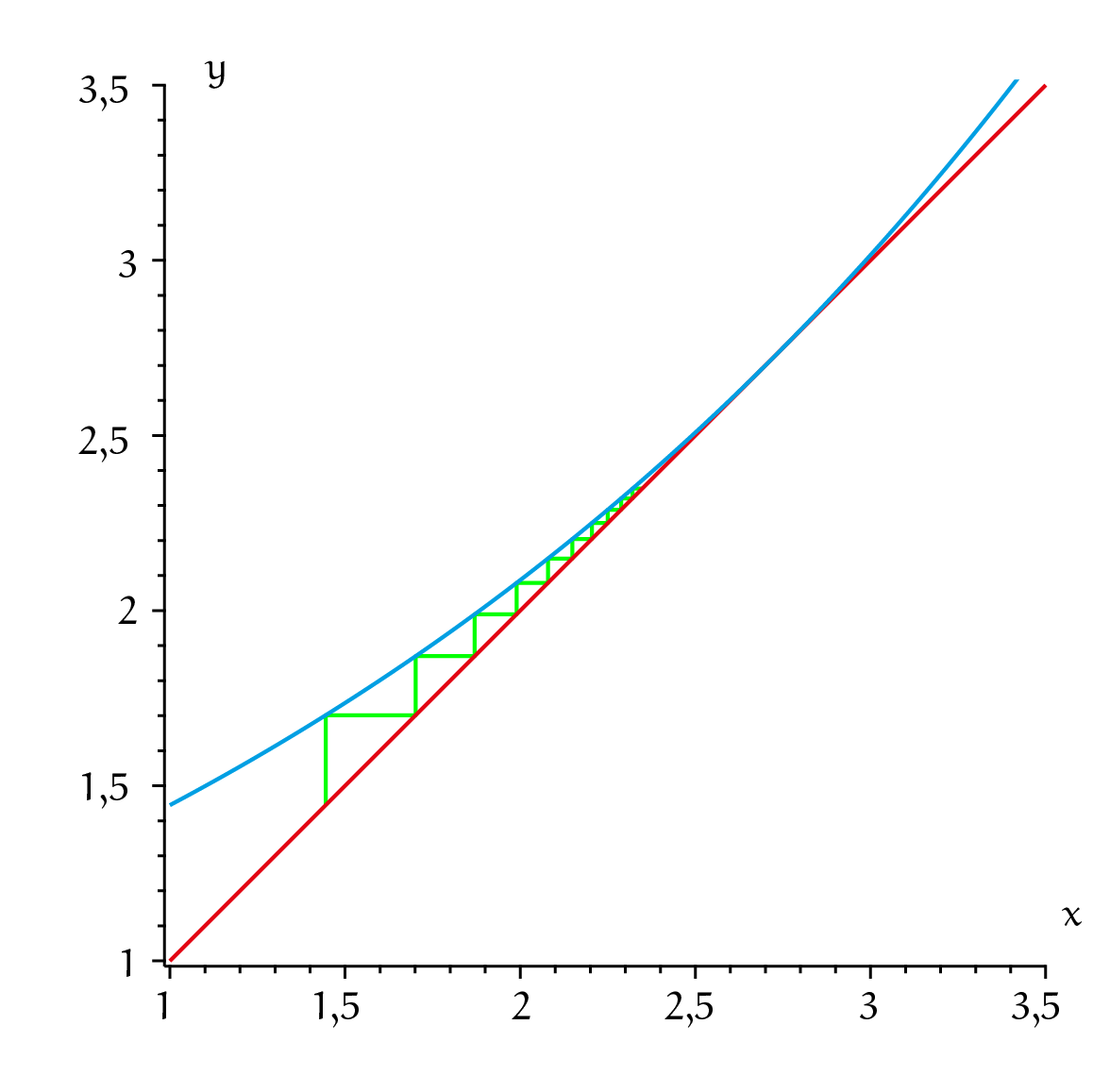
Kunnen we bewijzen dat dit inderdaad niet explodeert? Ja, dat kan. In grafiek 1 zie je de grafieken van $y = 1{,}25x$ (blauw) en $y = x$ (rood) in één plaatje. In de grafiek zijn ook de punten $(a_0, a_0), (a_0, a_1), (a_1, a_1), (a_1, a_2), \dots$ getekend, verbonden door rechte lijntjes (groen). Je ziet dat de twee grafieken elkaar snijden in een punt met coördinaten $(b, b)$ (die $b$ wordt straks belangrijk). De functie $1{,}25x$ is stijgend en daaruit volgt meteen dat voor elke $x$ met $x < b$ ook geldt dat $1{,}25x < 1{,}25b = b$. Omdat $1{,}25 < b$ volgt nu voor alle $n$ achtereenvolgens dat $a_n < b$.

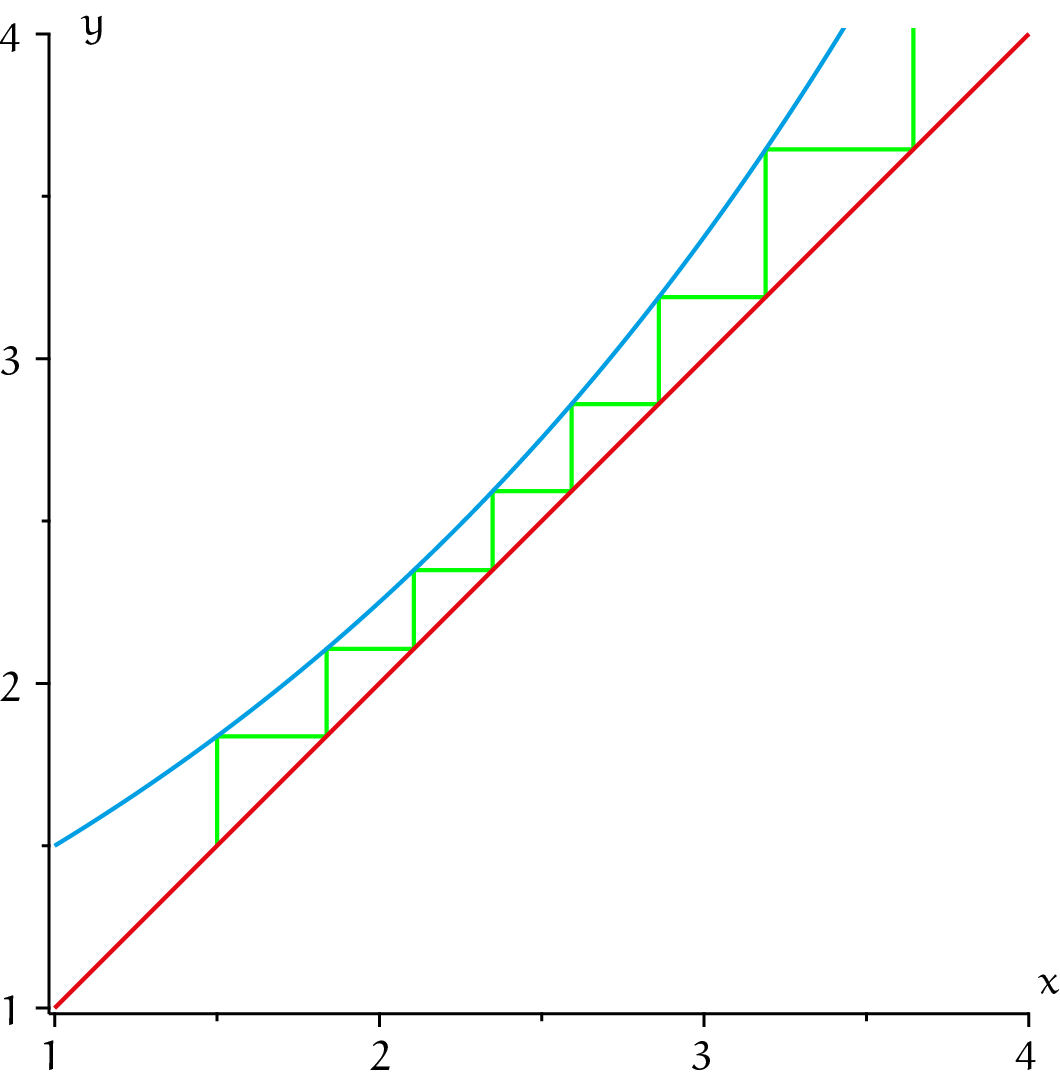
De rij blijft dus keurig begrensd. Hij convergeert naar $b$ en $b$ heeft de eigenschap dat $1{,}25b = b$; we kunnen nu afspreken dat die $b$ de waarde van de oneindige machtsverheffing van $a = 1{,}25$ is: $b = a^{\hat{}}a^{\hat{}}a^{\hat{}}\cdots$ Hoe bereken je $b$? Expliciet berekenen gaat niet maar je kunt $b$ benaderen door het machtsverheffen een paar keer uit te voeren. Bij $a = 1{,}25$ is $a_{20} =1{,}352203513$ een goede benadering. Je kunt een oneindige machtstoren $b = a^{\hat{}}a^{\hat{}}a^{\hat{}}\cdots$ niet expliciet uitrekenen, maar verrassend is, dat dit in ‘omgekeerde richting’ wel lukt: gegeven een zekere $b$, is er een eindige formule om $a$ te berekenen. Je kunt $b = a^{\hat{}}a^{\hat{}}a^{\hat{}}\cdots$ namelijk schrijven als: $b = a^{\hat{}}(a^{\hat{}}a^{\hat{}}a^{\hat{}}\cdots)$ en dankzij het feit dat er oneindig veel machtsverheffingen zijn, is het stuk binnen de haakjes ook $b$. Dus de vergelijking wordt: $b = a^{\hat{}}b$. Als je nu de linker- en de rechterkant verwisselt en beiden tot de macht $1/b$ verheft, krijg je: $a = b^{\hat{}}(1/b)$, een exacte, eindige formule voor $a$. Bijvoorbeeld, als $b = 2$ dan geldt $a = 2^{\hat{}}(1/2) = 2$. Voor $a = 2$ kunnen we hetzelfde doen als hierboven. We krijgen grafiek 2.

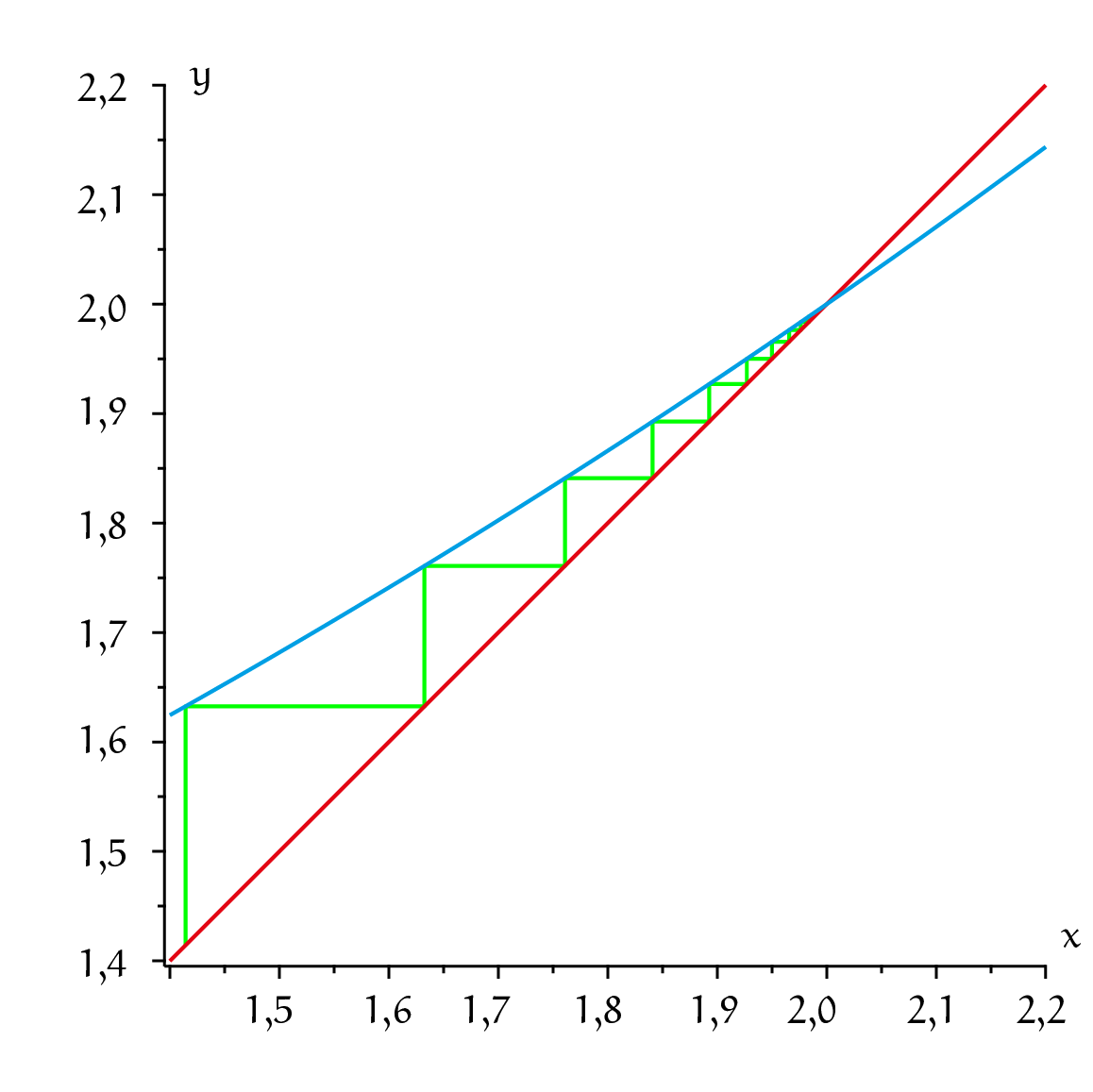
Dit betekent in wezen, dat de wiskundige bewerking ‘oneindig vaak machtsverheffen’ een inverse heeft, die deze bewerking ongedaan
maakt, namelijk door een getal $x$ te verheffen tot de macht $1/x$. Dit idee wordt verderop nog uitgewerkt.

We zien dat de rij bij $\sqrt2$ inderdaad naar $2$ convergeert. Dat geeft een mooie formule
$2^{\hat{}}2^{\hat{}}2^{\hat{}}\cdots = 2$. Wel oppassen: er geldt ook $\sqrt2 = 4^{\frac14}$ maar de gelijkheid
$2^{\hat{}}2^{\hat{}}2^{\hat{}}\cdots = 4$ geldt dus niet.

We kunnen ook starten met een getal tussen $0$ en $1$, bijvoorbeeld met $b =\frac12$ en dus $a=\left(\frac12\right)^2 = \frac14$. Omdat de grafiek van $\left(\frac14\right)^x$ dalend is krijgen we nu de spinneweb-achtige figuur in grafiek 3.

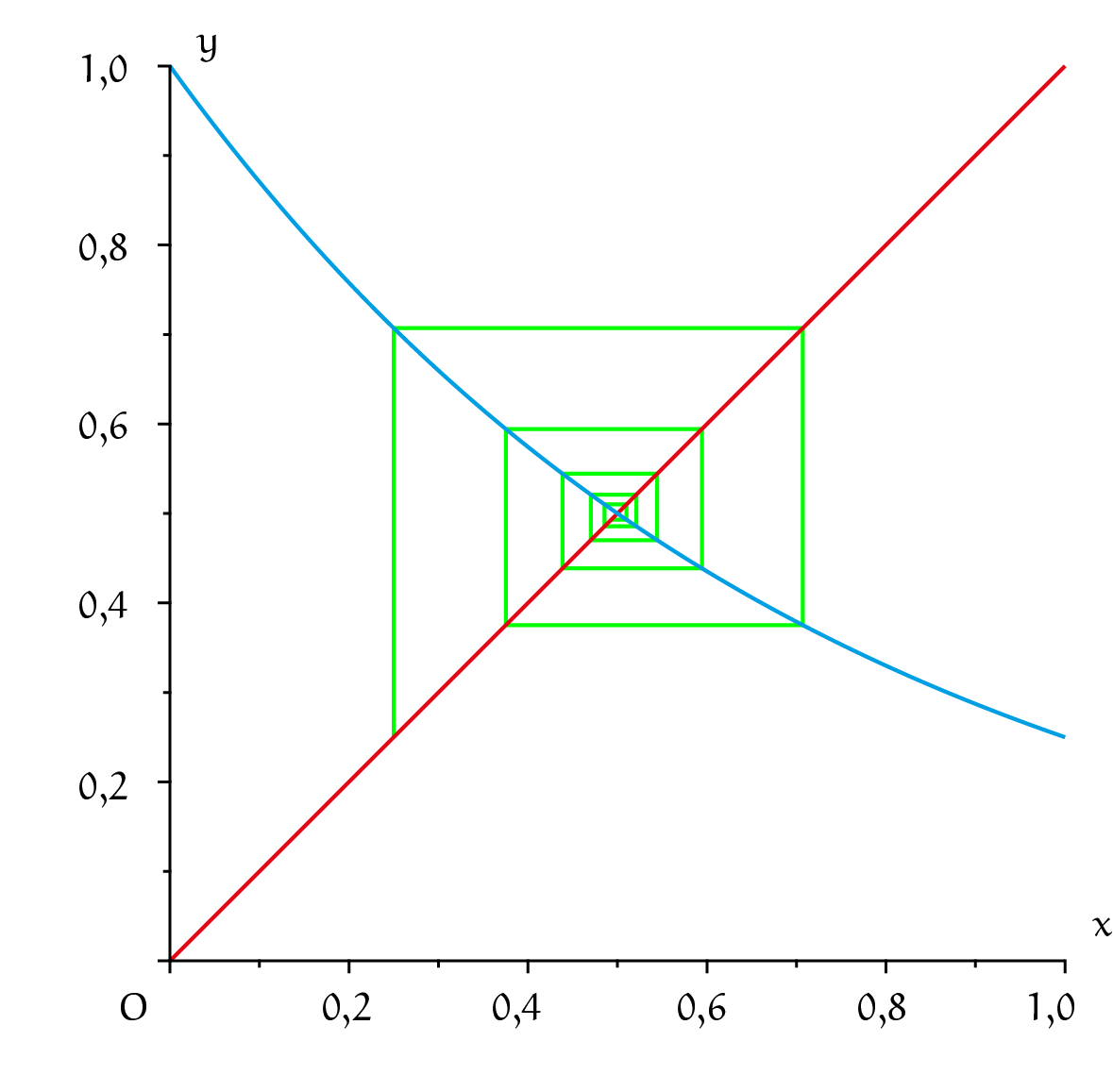
Er geldt inderdaad $${\frac14}^{{\frac14}^{{\frac14}^{\cdot^{\cdot^\cdot}}}} = \frac12.$$

Het breekpunt

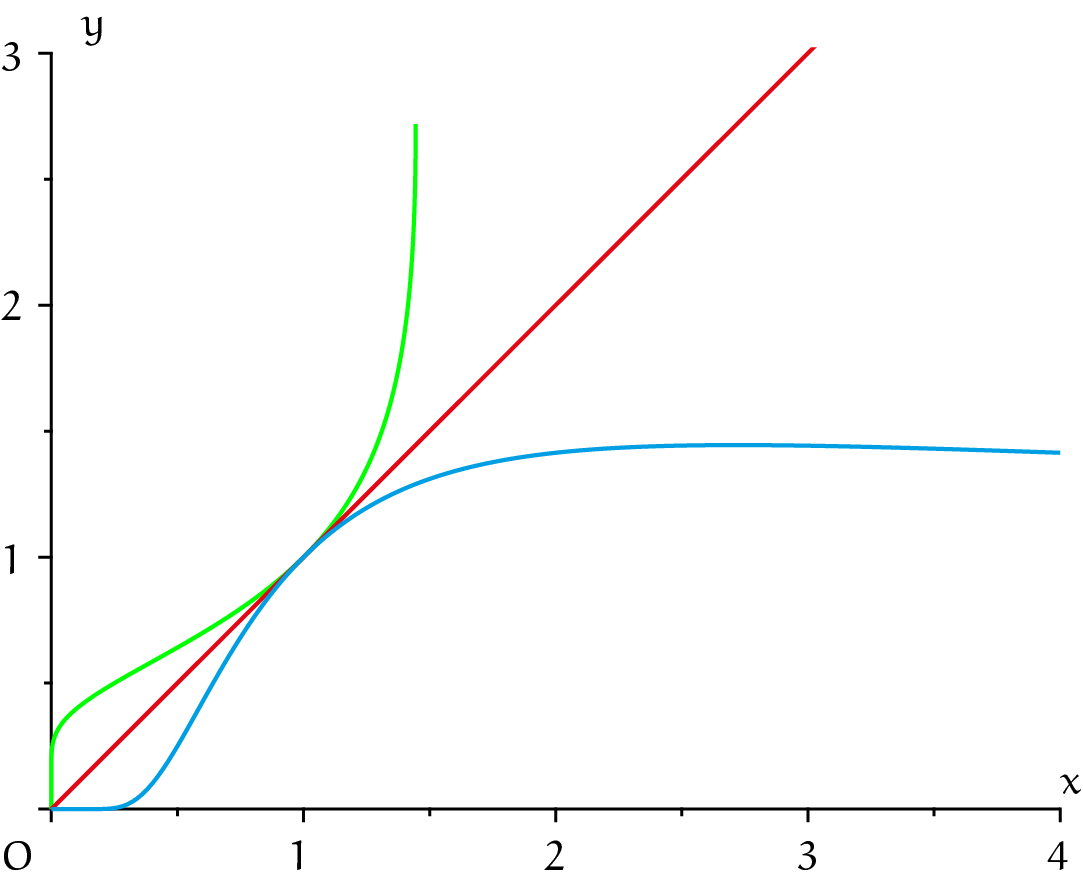
Maar goed, waar ligt nu het breekpunt? Welk getal bepaalt de grens tussen tam en explosief? Dat kunnen we uitvinden door naar de functie $g$ gegeven door $g(x) = x^{\frac{1}{x}}$ te kijken. De grafiek van die functie is in grafiek 4 getekend,
samen met de grafiek van $y = x$.

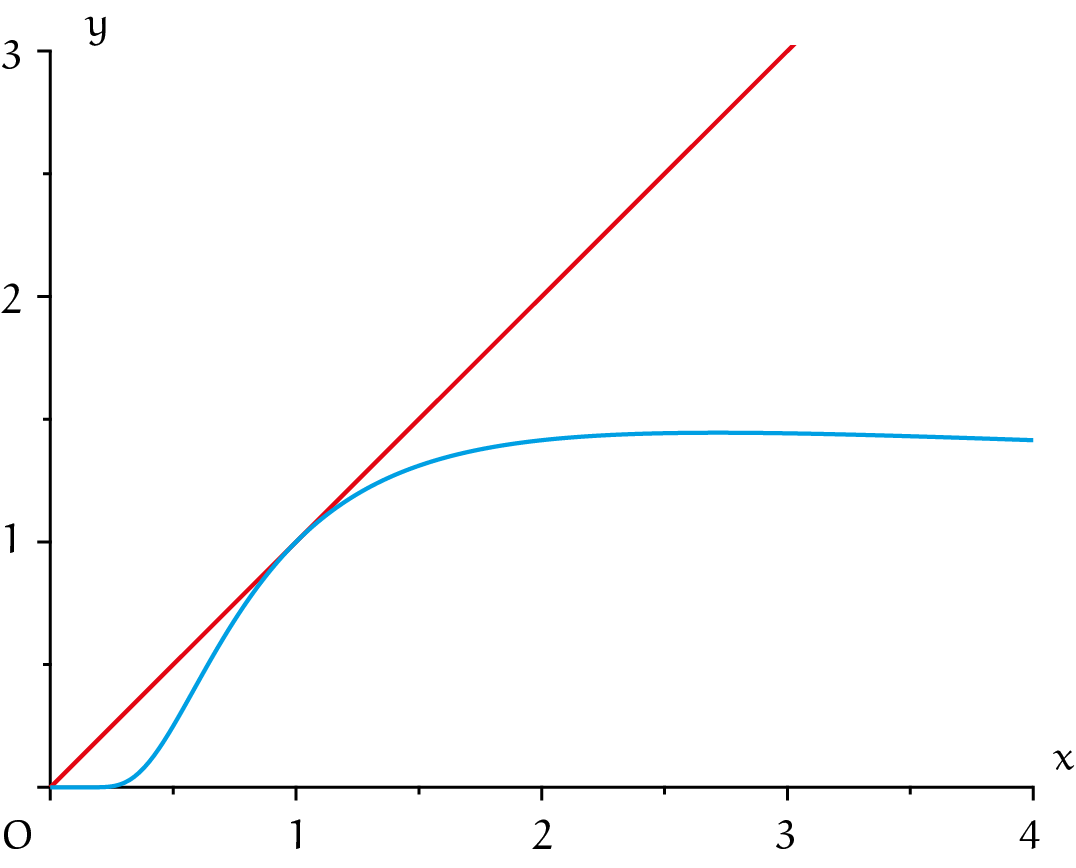
We zien meteen dat $g(b) \le b$ voor alle $b > 0$. Dat kun je ook uitrekenen.

Als $b > 1$ dan is $b^x$ stijgend en dus $b^{\frac{1}{b}} < b$ omdat $\frac{1}{b}<1$.

Als $b < 1$ dan is $b^x$ dalend en dus $b>b^{\frac{1}{b}}$ omdat $1<\frac{1}{b}$.

En natuurlijk geldt $g(1) = 1$. We zien dat zelfs $g(b) < b$ als $b \ne 1$.

De functie $g$ stijgt duidelijk tot $b = 2$, daarna ziet de grafiek er vlak uit maar omdat $g(2) = g(4) = \sqrt2$ zal er ergens tussen $2$ en $4$ een maximum optreden. Dat maximum vinden we door differentiëren:

$$g'(x)=x^{\frac{1}{x}}\cdot\frac{1}{x^2}\cdot(1-\ln x).$$

(Hint: schrijf $g(x) = {\rm e}^{\frac{1}{x}\ln x}$ en gebruik de kettingregel.)

We zien dat $g'(x) > 0$ als $x < {\rm e}$ en $g'(x) < 0$ als $x > {\rm e}$. Er is dus een maximum, en dat maximum treedt op bij $\rm e$. Bij $b = {\rm e}$ hoort $a={\rm e}^{\frac{1}{\rm e}} \approx 1{,}444667861$.

Voor deze waarde van $a$ is de lijn $y = x$ een raaklijn aan de grafiek van $a^x$, en het raakpunt is $({\rm e}, {\rm e})$. Zie grafiek 5.

Conclusies

Nu kunnen we wat conclusies trekken. We definiëren de functie $f$ door

$$f(x) = x^{x^{x^{\cdot^{\cdot^\cdot}}}}$$

Als $1 < a < {\rm e}^{\frac{1}{\rm e}}$ dan zijn er twee waarden van $b$ met $b^{\frac{1}{b}} = a$ ofwel $a^b = b$. Als we $f(a)$ bepalen door middel van de rij $a, a^{\hat{}}a, a^{\hat{}}a^{\hat{}}a, \dots$ dan zien we dat $f(a)$ gelijk is aan de kleinste van die twee $b$s (zoals we gezien hebben bij $a = \sqrt2$, met $b_1 = 2$ en $b_2 = 4$.

Als $0 < a \le 1$ dan is er één $b$ met $b^{\frac{1}{b}} = a$ en hier geldt $f(a) = b$.

Als $a = {\rm e}^{\frac{1}{\rm e}}$ dan is $f(a)$ gelijk aan $\rm e$.

Als $a > {\rm e}^{\frac{1}{\rm e}}$ dan is er geen $b$ met $b^{\frac{1}{b}} = a$ ofwel $a^b = b$. In dat geval explodeert het proces, zoals in grafiek 6 te zien is voor $a = 1{,}5$.

Maar we weten nu meer over de functie $f$. Zijn domein is het interval $\left(0, {\rm e}^{\frac{1}{\rm e}}\right]$ en hij is de inverse van de functie $g$, waarbij we het interval $\left(0, {\rm e}\right]$ als domein nemen.

De functie $g(x)$ is redelijk eenvoudig te bestuderen en elke eigenschap van $g$ kun je vertalen naar een eigenschap van $f$ door die als het ware te spiegelen in de lijn $y = x$. Zie ook grafiek 7.

Opgave 1 Bewijs dat $\lim_{x\downarrow 0}g(x)=0$.

Als we apart definiëren dat $g(0) = 0$ wordt $g$ dus continu op [0,1]$.

Opgave 2 Bewijs dat ook $\lim_{x\downarrow 0}g'(x)=0$.

De grafiek van $g$ loopt dus naar $0$ toe vrijwel horizontaal. Conclusie: de grafiek van $f$ loopt naar $0$ toe vrijwel verticaal.

Hoe horizontaal de grafiek van $g$ naar $0$ toe gaat lopen kun je zien aan de volgende opgaven.

Opgave 3 Bewijs: voor elk natuurlijk getal $n$ geldt $\lim_{x\downarrow 0}g(x)\cdot x^n = 0$. Opgave 4 Zoek uit of de grafiek van $f$ een buigpunt heeft en zo ja, bepaal dat buigpunt. Waar is de grafiek van $f$ convex? Waar is hij concaaf?

(Héél erg horizontaal dus.)

De raaklijn aan $g$ bij ${\rm e}^{\frac{1}{\rm e}}$ loopt horizontal; de raaklijn aan $f$ bij $\rm e$ loopt dus verticaal.