Een computer is eigenlijk een heel grote en luxueus uitgevoerde rekenmachine. In het hart van de computer zit een rekenprocessor die het grootste deel van de tijd stilstaat, ook bijvoorbeeld op dit moment, nu je deze tekst leest.

De kleine programmaatjes die we hieronder laten zien, zullen de processor juist hard laten werken. Ze zijn zo bedacht dat ze er telkens – op onze computer – ongeveer een seconde over doen. Natuurlijk is dit wel afhankelijk van de snelheid van je processor.

Stel je draait op een 2.5 GHz processor (dit is een processor die 2,5 miljard bewerkingen per seconde kan doen). In dat geval zal je nooit meer dan 2,5 miljard berekeningen per seconde kunnen uitvoeren. Meestal is dit aanzienlijk minder, zeker als we op een gegeven ogenblik met grotere getallen gaan werken.

Wat er binnen in een computer gebeurt is een gecompliceerd proces. We zullen ons bij het versnellen van berekeningen vooral richten op het verbeteren van wiskundige algoritmes. Vaak zijn er verbeteringen door te voeren door op een betere wijze gebruik te maken van het geheugen. Ook dat kan ingewikkeld zijn. We zullen daar aandacht aan besteden als het voor de hand ligt.

Alle programma's staan op onze website pyth.eu als Jupyterfiles. Je kan in een Jupyterfile in één keer voor elk programma regelnummmers krijgen door bovenaan bij View Toggle line numbers aan te passen

Tellen tot 7 400 000

In het eerste programma gaan we tellen tot $7{,}4$ miljoen. Dit doen we door steeds de waarde $1$ bij een getal op te tellen.

.

Toelichting op dit programma

Het is een goed idee om bij het begin aan jezelf en anderen te vertellen wat een programma gaat doen. We schrijven deze toelichting achter een hekje: alle tekst achter # wordt genegeerd door Python.

In regel $3$ wordt de module time geladen. Een module is een bestand waar allerlei programma's in zijn opgeborgen, meestal met één onderwerp. De module time bevat een programma waarmee je de tijd kan meten die de processor gebruikt voor een programma. In regel $4$ wordt de functie process_time() uit deze module uitgevoerd. Deze functie heeft als uitvoer de tijd die de processor sinds de laatste start van de computer werkzaam is geweest.

Regel $5$ bevat een toekenning aan een variabele. In onze programma's maken we onderscheid tussen variabelen die gedurende het programma mogen veranderen, en variabelen die dit niet mogen. Deze laatste variabelen zullen we schrijven met hoofdletters. We noemen ze constanten. (In het bovenstaande programma is de constante HERH het aantal HERHalingen.) We zetten constantes bovenaan, zodat we deze variabelen gemakkelijk kunnen vinden.

In regel $6$ wordt aan de variabele som de waarde $0$ toegekend. In regel $7$ wordt de constante HERH gebruikt. De uitdrukking range(a, b) is niets anders dan een lijst met de opeenvolgende getallen $a, a + 1, a + 2, … , b – 2, b – 1$, anders gezegd, groter dan of gelijk aan $a$ en kleiner dan $b$. De gehele regel for i in range(0, HERH): laat de regels er onder (die vier spaties inspringen) een aantal keren uitvoeren, voor de opeenvolgende waarden $0, 1, 2, ..., HERH-1$, in het totaal dus HERH maal. 

In regel $8$ wordt waarde van de variabele som verhoogd met $1$. Dit resultaat verkrijg je ook als je regel $8$ vervangt door: som = som + 1.

Regel $9$ is vergelijkbaar met regel $2$. Alleen de processor is nu wat langer werkzaam geweest. In regel $10$ wordt afgedrukt wat er tussen de () staat achter print. In de Jupyter-omgeving gebeurt dat recht onder de code.

Hier wordt dus het tijdsverschil t1-t0 in secondes afgedrukt, dat de processor aan dit programma heeft gerekend.

Opdracht

a)    Het kan gebeuren dat als je het bovenstaande programma uitvoert (met "Run", of "Shift-Return") dat er een getal komt te staan dat afwijkt van de $1$ seconde. Als je het programma nogmaals uitvoert zul je zien dat deze tijdsduur net iets verschilt.

b)    De processor doet meer dan alleen maar dit Python-programma uitvoeren. We mogen er echter wel van uitgaan dat de processor voornamelijk met het uitvoeren van het Python-programma bezig is. Mocht jouw uitkomst meer dan $10$% van de $1$ seconde verschillen, pas dan de constante HERH aan zodat de uitvoer hooguit $10$% afwijkt van 1 seconde, ofwel zodat de uitvoer tussen $0{,}9$ en $1{,}1$ seconde ligt. Op deze manier weet je hoeveel tijd jouw computer ongeveer nodig heeft voor het programma.

Vermenigvuldigen met 1 kost tijd! 

In het volgende programma gaan we in plaats van sommeren kijken naar vermenigvuldigen. In plaats van de variabele som gebruiken we de variabele prod. Steeds vermenigvuldigen we prod met $1$.

 

We hebben de module time opnieuw geimporteerd. Dit is niet nodig, maar het is handig als je alleen met het tweede programma wilt experimenteren.

Je ziet dat dit programma iets sneller is dan het eerste programma, dat $12 500 000$ keer iets optelt. Dat wordt anders als je met $2$ gaat vermenigvuldigen.

In regel $8$ wordt prod steeds vermenigvuldigd met $1$. Deze regel kan ook worden geschreven als: $prod = prod * 1$.

Opdracht

a)    Mocht je uitvoer niet tussen $0{,}9$ en $1{,}1$ seconde liggen, pas HERH aan zo dat de uitvoer wel in deze marge terecht komt.

b)    Vervang regel $7$ door prod = prod * 1+1-1. Je ziet dat de processor meer tijd kwijt is, doordat HERH-maal ook nog de waarde $1$ opgeteld en afgetrokken moet worden.

Grotere getallen

In het volgende programma krijgt de grootte van getallen invloed op de snelheid. De regel prod *= 1 vervangen we door prod *= 2. We berekenen $2^{200 000}$.

 

Regel 13 bepaalt het aantal cijfers van het laatste getal. Er wordt gebruik gemaakt van twee functies in de math module: log en ceil. De functie log heeft een of twee invoerwaarden. Met één invoerwaarde is de functie log hetzelfde als de natuurlijke logaritme. Met twee invoerwaarden is log(m,n) hetzelfde als $^n\log(m)$.

Het programma is $7 400 000 / 200 000 \approx 40$ maal zo traag. Dat heeft vooral te maken met het feit dat er al behoorlijk grote getallen gegenereerd worden. $2^{200 000}$ is een getal bestaande uit ongeveer $60 000$ cijfers.

Opdracht:

Pas HERH weer aan zodat je ongeveer 1 seconde rekentijd gebruikt.

Berekening van 2^EXP

Mocht je $2^k$ willen berekenen voor grotere waarden van $k$ binnen $1$ seconde, dan is er een snellere methode.

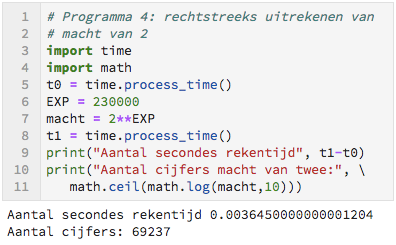
Dit maakt aanzienlijk uit!

Opdracht

Pas de constante EXP aan zodat je weer rond de $1$ seconde rekentijd gebruikt.

Berekening van grondtal^EXP

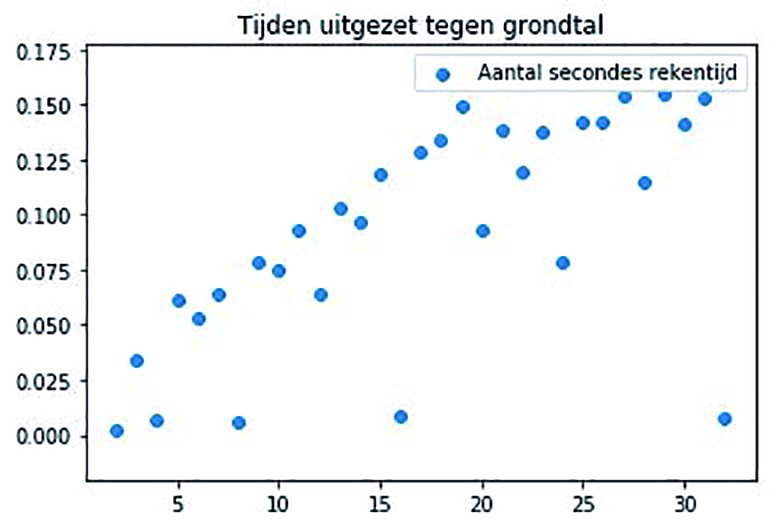
We gaan nu voor een heel scala aan grondtallen de berekening grondtal^EXP uitvoeren, en bepalen we hoelang dat duurt. In een plot zetten we deze tijden uit tegen de grondtallen.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Opmerkingen

1)    Het programma duurt ongeveer 1 minuut.

2)    Het kan zijn dat je alleen maar <matplotlib.figure.Figure at 0x...> ziet staan. Doe dan nog eens de toetsencombinatie Shift + Enter!

In regel 3 wordt de module matplotlib genoemd. Dit is een grafische bibliotheek met functies waarmee allerlei grafieken kunnen worden getekend. In het bijzonder gebruiken we pyplot, een deelbibliotheek. Daarachter staat as plt. Dat betekent dat we niet steeds matplotlib.pyplot hoeven te schrijven, maar slechts plt. (Het is een soort van alias.)

In regel 7 introduceren we de lijst (list) Tijden. De lege lijst noteren we met []. In regel 13 wordt er een element toegevoegd aan Tijden. Dit zijn steeds de processortijden om de berekening grondtal^EXP uit te voeren. 

In regel 8 introduceren we Xset. Xset is de verzameling getallen 2 t/m 32. Xset wordt op twee plaatsen gebruikt, namelijk in regel 9 en regel 15.

In de regels 15 t/m 18 wordt gebruik gemaakt van matplotlib (plt). De belangrijkste regel is regel 15. We kiezen voor scatter, om losse punten te kunnen weergeven. Later zullen we ook andere toepassingen bekijken. Regel 17 plaatst de getallen bij de assen.

Je ziet dat de plot er contra-intuïtief uitziet. Je verwacht dat naarmate het grondtal toeneemt ook de tijd om grondtal^EXP uit te rekenen zal toenemen. Dat is niet het geval. Voor de machten van 2 (2, 4, 8, 16 en 32) is de tijd om de berekening uit te voeren nagenoeg 0. Voor 12, 20 en 24 is de tijd dat de berekening kost ook beduidend kleiner dan belendende grondtallen.

De som van kwadraten

We gaan nu de som van acht miljoen kwadraten berekenen.

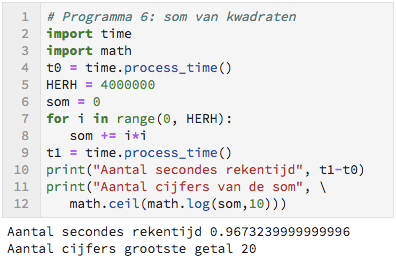
In de for-loop wordt nu gebruik gemaakt van het feit dat de variabele i achtereenvolgens de waarden 0, 1, 2, ... aanneemt. De variabele som wordt steeds verhoogd met de waarde i*i.

Opdracht

Pas de constante HERH aan zo dat de uitvoer tussen 0,9 en 1,1 ligt. We kunnen in plaats van i*i ook gebruik maken van i**2 (dit is Pythoncode voor i²). Vervang regel 7 door som += i**2

Wat is je conclusie? Doe hetzelfde voor derde machten.

De faculteit

Nu gaan we kijken naar faculteiten. n! = 1 × 2 × 3 × … × n. In de wiskunde komt n! veel voor. Het zou mooi zijn wanneer we dit snel exact kunnen berekenen. We kijken hoever we in 1 seconde kunnen komen.

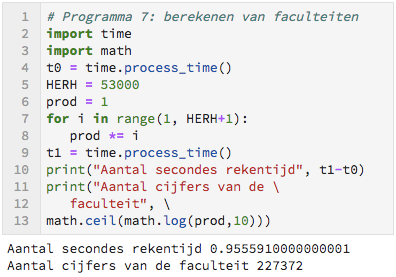
Opdracht

a)    Pas de constante HERH aan zo dat de uitvoer tussen 0,9 en 1,1 ligt.

b)    Maakt het uit om in plaats van $1 \times 2 \times 3 \times \dots \times n$ achteraan te beginnen en $n \times (n-1) \times (n-2) \times \dots \times 1$ te berekenen?

Fibonacci

In Pythagoras is diverse malen geschreven over de rij van Fibonacci, onder andere in de afgelopen jaargang (Pythagoras 57-5/6). De startwaarden zijn 0 en 1. Het volgende getal wordt steeds berekend als de som van de twee laatste getallen.

In het programma is a steeds het voorlaatste getal en b het laatste getal. Het nieuwe getal in de rij is a + b. Hierna moeten de getallen opgeschoven worden. Op de plaats van a komt b en op de plaats van b komt a + b. Dit gebeurt op de regels 9, 10 en 11. Er wordt gebruik gemaakt van de hulpvariabele c.

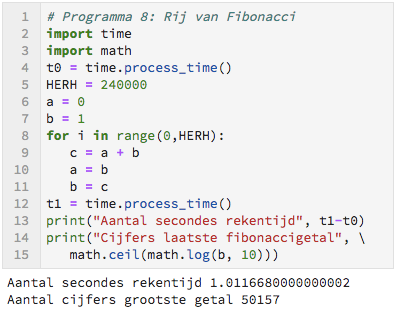
Opdracht

a)    Pas HERH aan zo dat de uitvoer opt jouw computer tussen 0,9 en 1,1 ligt.

b)    Vervang regel 8 door: c = 1*a + 1*b Wat voorspel je dat dit met de tijd doet?

De vermenigvuldigingsvariant van Fibonacci

In plaats van telkens de laatste twee getallen op te tellen vermenigvuldigen we deze en tellen 1 bij het product op, dus:

0, 1, 0×1+1, 1×1+1, 1×2+1, 2×3+1, 3×7+1, etcetera

Vooraf een waarschuwing! Kies HERH heel klein, anders moet je heel lang wachten en kan je computer zelfs vastlopen. Als je te lang moet wachten, kan je bovenaan in je Jupyterscherm op het vierkantje klikken. Daarmee wordt de berekening onderbroken.

Het onderstaande programma doet een beetje denken aan Fibonacci, maar dan met vermenigvuldigingen. Hoe moet HERH worden gekozen, zo dat je 1 seconde kunt rekenen.

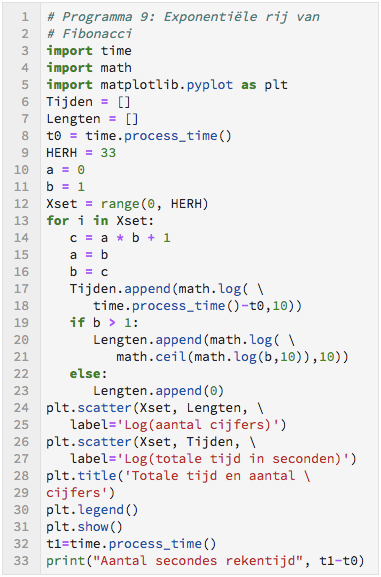
In de grafiek hierboven zijn de logaritme van het aantal cijfers van de Fibonacci variant en de logaritme van het totaal aantal seconden dat het kost om alle berekeningen uit te voeren.

Opdracht

a)    Je ziet dat we ver over de 1 seconde heen gaan. Hoe groot moet je HERH kiezen om in het totaal 5 minuten te rekenen?

b)    Wanneer bereik je een biljoen (= 10¹²) cijfers? Al deze cijfers moeten worden opgeslagen in het geheugen. Er van uitgaande dat je met 1 kB ongeveer 2400 cijfers kunt opslaan (elke byte kan 0 t/m 255 opslaan, met 1 kB kun je 256¹⁰⁰⁰ ≈ 10²⁴⁰⁰ opslaan), heb je voor een biljoen cijfers 420 GB geheugen nodig. Je hebt zelfs driemaal zoveel nodig om a, b en c op te slaan. In weinig computers is zoveel intern geheugen aanwezig. Met dit programma loop je heel snel tegen de grenzen van je computer aan.

Uitdaging

Door dieper op een berekening in te gaan, kan je een programma versnellen. Als je snellere of betere programma's hebt kunnen schrijven voor bovenstaande opdrachten, willen we deze graag ontvangen. Ze worden op de website gepubliceerd, doorgemeten en besproken.

De code behorend bij dit artikel krijg je door op de knop "Bekijk oplossing" te klikken.

Bekijk oplossing