Vijf kabouters worden gegijzeld door de gemene Voldemort. Ze krijgen de kans om vrij te komen. Daarvoor moeten ze een moeilijk raadsel oplossen.

Voldemort is de ultieme vertegenwoordiger van het kwaad. De kabouters zullen een ongelukkig lot tegemoet gaan, behalve… als ze in staat zijn een moeilijk raadsel op te lossen. Voldemort heeft vijftien kaboutermutsen: vijf rode, vijf blauwe en vijf gele. Hij zegt tegen de kabouters: 'Morgen plaats ik jullie in twee rijen: in rij $1$ staan twee kabouters, in rij $2$ staan drie kabouters. Kabouters in dezelfde rij kunnen elkaar niet zien. Wel kan iedereen de kabouters in de ándere rij zien.' Terwijl Voldemort zijn vijftien mutsen laat zien, vervolgt hij: 'Ik zal ieder van jullie één van deze mutsen op het hoofd zetten. Zodra ik een signaal geef, raadt iedereen tegelijkertijd zijn eigen mutskleur. Als ten minste één van jullie zijn mutskleur goed raadt, laat ik jullie vrij.'

Tot het moment dat de kabouters in de twee rijen worden opgesteld, kunnen de kabouters met elkaar overleggen. Daarna niet meer: zodra de mutsen zijn verdeeld, is elke vorm van communicatie, ook non-verbaal, verboden. De slimme kabouters bedenken een strategie waarmee ze gegarandeerd vrij zullen komen. Hoe luidt die strategie?

 

Oplossing

Om te beginnen nummeren de kabouters de drie mutskleuren: rood = $0$, blauw = $1$ en geel = $2$. De kabouters spreken af dat de twee in de eerste rij A en B heten, en de drie in de tweede rij C, D en E. De vijf mutskleuren van A, B, C, D en E  noteren ze met achtereenvolgens $a$, $b$, $c$, $d$ en $e$. Om de strategie van de kabouters te begrijpen, moet je weten wat 'rekenen modulo 3' betekent; zie daarvoor het kader.

	RekEneN moDuLO 3 Als het nu tien uur 's ochtends is, staat de kleine wijzer van een (analoge) klok op $10$. Over acht uur staat de wijzer op $6$, nog eens acht uur later op $2$. Wiskundigen zeggen dat $10 + 8$ gelijk is aan '$6$ modulo $12$'. En $10 + 16$ is gelijk aan '$2$ modulo $12$'. Rekenen 'modulo $3$' gaat net zo, alleen moet je je geen klok voorstellen met de getallen $1$ tot en met $12$, maar met de getallen $0$, $1$ en $2$. Als je 'modulo $3$' rekent, is elk veelvoud van $3$ (dus $3, 6, 9, \dots$) gelijk aan $0$. De  getallen $4, 7, 10, \dots$ zijn allemaal gelijk aan $1$, en $5, 8, 11, \dots$ zijn alle gelijk aan $2$. Een paar rekenvoorbeelden: $1 + 1 = 2\ (mod\ 3)$, $1 + 2 = 0\ (mod\ 3)$, $2 + 2 = 1\ (mod\ 3)$. Hiernaast zie je een opteltabel voor het rekenen modulo $3$.

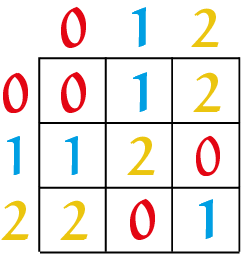De winnende strategie gaat als volgt. Kabouter C raadt kleur $a$, D raadt kleur $b$ en E raadt kleur $a + b\ (mod\ 3)$. Als ten minste één van hen zijn mutskleur goed raadt, doet het er niet toe wat A en B raden – de vrijlating is dan al gegarandeerd. A en B veronderstellen daarom dat C, D en E het allemaal fout hebben: $a \neq c$, $b \neq d$ en $a + b \neq e\ (mod\ 3)$. Welke strategie kunnen A en B nu hanteren waarmee ze er zeker van zijn dat minstens één van hen het goede antwoord geeft? Vanwege de aanname $a \neq c$ blijven er voor A's muts twee kleuren over; noem die kleuren $x$ en $x'$. En vanwege $b \neq d$ blijven ook voor B's muts twee kleuren over; noem die $y$ en $y'$. In totaal zijn er nu vier mogelijke mutsverdelingen voor A en B: 

• A heeft $x$ en B heeft $y$;
• A heeft $x'$ en B heeft $y$;
• A heeft $x$ en B heeft $y'$;
• A heeft $x'$ en B heeft $y'$.

De kabouters berekenen van elke mogelijkheid de som: $x + y\ (mod\ 3)$, $x' + y\ (mod\ 3)$, $x + y'\ (mod\ 3)$ en $x' + y’\ (mod\ 3)$. Onder deze vier uitkomsten komen alle mogelijke waarden ($0$, $1$ en $2$) voor: twee waarden komen één keer voor, één waarde komt twee keer voor. Anders gezegd: neem je in de tabel (in het kader) twee rijen en twee kolommen, dan bevatten de vier kruispunten samen altijd alle drie de kleuren.

Vanwege de veronderstelling $a + b \neq e\ (mod\ 3)$ kunnen de kabouters dus één of twee van de vier mogelijke mutsverdelingen uitsluiten. Er blijven dus twee of drie mogelijke mutsverdelingen over.

A en B spreken nu het volgende af. Als er twee mutsverdelingen overblijven, kiest A zijn kleur in de mutsverdeling waarvan de som het kleinst is, en B kiest zijn kleur in de mutsverdeling waarvan de som het grootst is. Precies één van hen raadt zijn mutskleur dan juist. 

Als er drie mutsverdelingen overblijven, nemen ze de mutsverdeling die hoort bij de som die slechts één keer voorkomt. Beide kabouters noemen hun mutskleur dan correct.

VoOrbEeld 1

De kabouters C, D en E (die A en B zien) zeggen achtereenvolgens $0$, $1$ en $1$. Kabouter E heeft het goed en dus komen de kabouters vrij. 

Hoe redeneren A en B (die C, D en E zien)? Ze veronderstellen dat $a \neq 1$, $b \neq 2$ en $a + b \neq 1$. Uit $a \neq 1$ en $b \neq 2$ concluderen ze dat hun mutsverdeling één van de volgende mogelijkheden is:

• A heeft $0$ en B heeft $0$, er geldt $0 + 0 = 0\ (mod\ 3)$;
• A heeft $0$ en B heeft $1$, er geldt $0 + 1 = 1\ (mod\ 3)$;
• A heeft $2$ en B heeft $0$, er geldt $2 + 0 = 2\ (mod\ 3)$;
• A heeft $2$ en B heeft $1$, er geldt $2 + 1 = 0\ (mod\ 3)$.

Omdat bovendien $a + b \neq 1$, kunnen ze de tweede optie wegstrepen. Van de drie mogelijkheden die overblijven, komt de som $2$ slechts eenmaal voor. A noemt dus $2$, B noemt $0$. Ze hebben het allebei fout. De reden dat de handelwijze van A en B spaak loopt, is dat hun veronderstelling niet klopt: niet alle drie de kabouters in de tweede rij geven een fout antwoord.

VOorbEeld 2

C, D en E zeggen achtereenvolgens $0$, $1$ en $1$: allemaal fout.

A en B veronderstellen dat $a \neq 1$, $b \neq 2$ en $a + b \neq 0$. Uit $a \neq 1$ en $b \neq 2$ concluderen ze dat hun mutsverdeling één van de volgende
mogelijkheden is:

• A heeft $0$ en B heeft $0$, er geldt $0 + 0 = 0\ (mod\ 3)$;
• A heeft $0$ en B heeft $1$, er geldt $0 + 1 = 1\ (mod\ 3)$;
• A heeft $2$ en B heeft $0$, er geldt $2 + 0 = 2\ (mod\ 3)$;
• A heeft $2$ en B heeft $1$, er geldt $2 + 1 = 0\ (mod\ 3)$.

Omdat bovendien $a + b \neq 0$, kunnen ze de eerste en laatste optie wegstrepen. A gaat nu uit van de tweede optie en zegt dus $0$, B gaat uit van de derde optie en zegt dus ook $0$. 

Kabouter A raadt zijn mutskleur dus correct.

VoOrbeEld 3

C, D en E zeggen achtereenvolgens $0$, $2$ en $2$: allemaal fout. 

A en B veronderstellen dat $a \neq 2$, $b \neq 1$ en $a + b \neq 1$. Uit $a \neq 2$ en $b \neq 1$ concluderen ze dat hun mutsverdeling één van de volgende mogelijkheden is:

• A heeft $0$ en B heeft $0$, er geldt $0 + 0 = 0\ (mod\ 3)$;
• A heeft $0$ en B heeft $2$, er geldt $0 + 2 = 2\ (mod\ 3)$;
• A heeft $1$ en B heeft $0$, er geldt $1 + 0 = 1\ (mod\ 3)$;
• A heeft $1$ en B heeft $2$, er geldt $1 + 2 = 0\ (mod\ 3)$.

Omdat bovendien $a + b \neq 1$, kunnen ze de derde optie wegstrepen. Er blijven drie mogelijkheden over. A en B kiezen voor de tweede optie, want de som $2$ komt slechts eenmaal voor. A noemt dus $0$, B noemt $2$.

Allebei goed!