Opgave 1

Neem de $30^{\rm o}$-draaiing van de punten uit de hint. Bepaal/teken van elk tweetal punten de middelloodlijn, de lijn van punten met gelijke afstand tot die twee punten. We krijgen dan de volgende figuur, met in principe tien middelloodlijnen; daarvan vallen er twee samen.

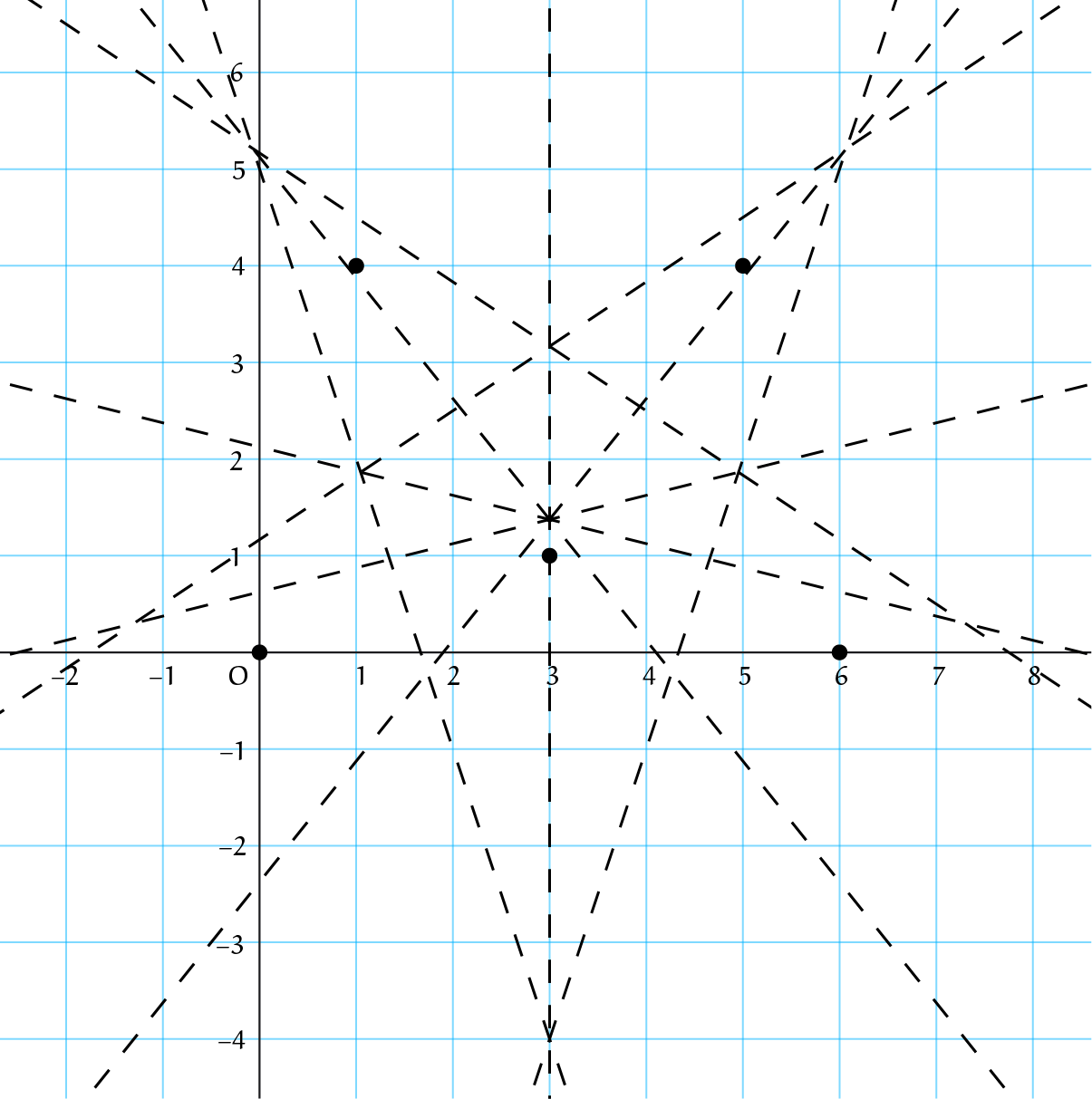
Als we de snijpunten van deze negen middelloodlijnen nagaan, resulteert dit in het volgende Voronoidiagram.

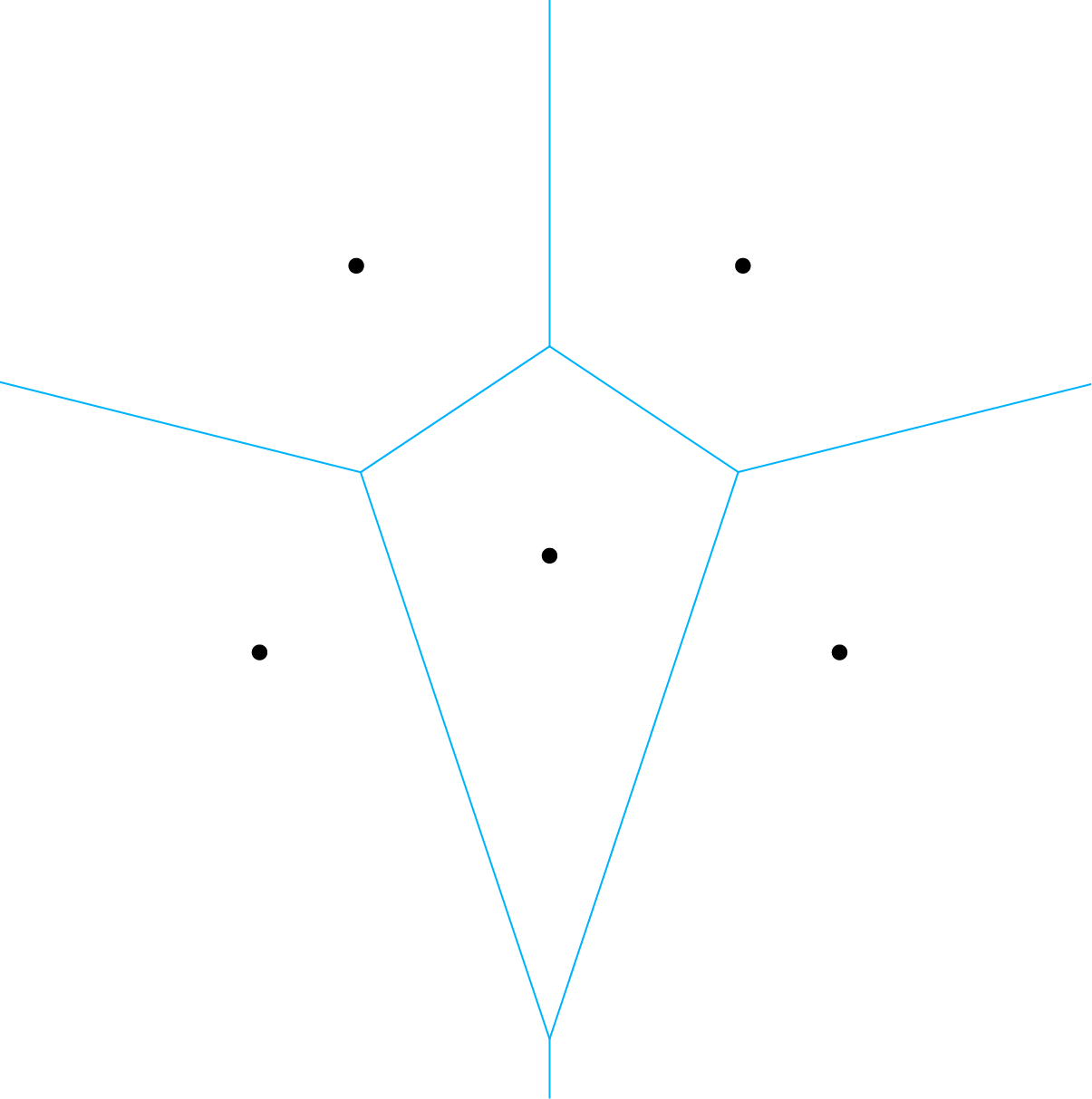
En met de $30^{\rm o}$-terugdraaiing:

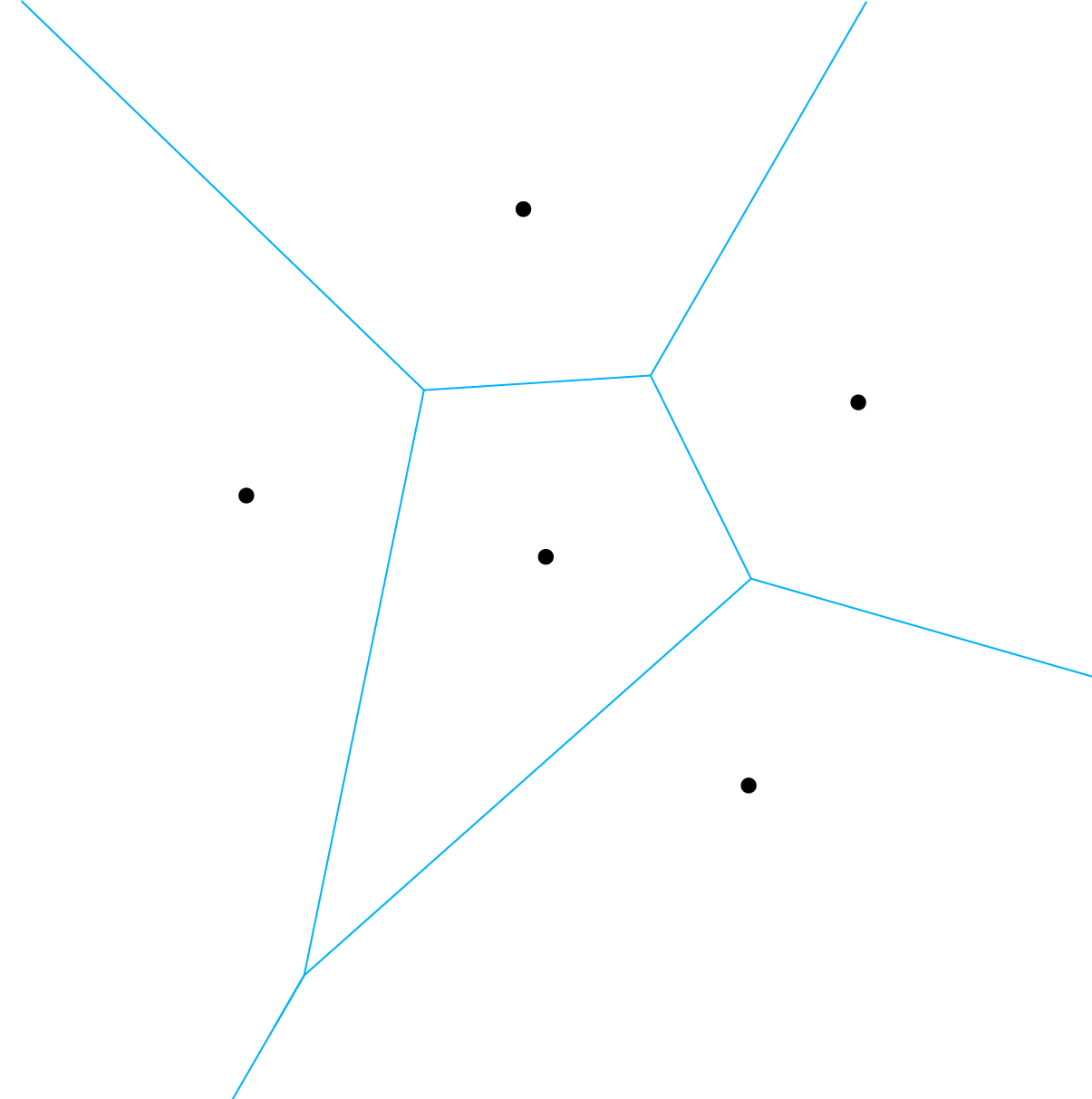
Opgave 2

De drie Voronoikrommen $AB$, $AC$ en $BC$ bestaan alle drie uit een afwisseling van lineaire en parabolische stukken. Voor $2 \le x \le 2\tfrac{1}{2}$ bijvoorbeeld geldt voor de Voronoikromme van $A$ en $C$:

$\sqrt{(x-2)^2+(y-1)^2}=3-x$.

Links en rechts kwadrateren geeft

$y^2-2y-4+2x=0$.

Dit oplossen voor $y$ levert

$y=1-\sqrt{5-2x}$.

(Let op: de ‘negatieve tak’ van de parabool nemen.)

Tussen het tweede en derde gegeven punt op de Voronoikromme van $A$ en $C$, dus voor $3\le x\le 4$ is het eenvoudig. Daar is de kortste afstand tot beide eilanden alleen van één variabele afhankelijk:

$x-2 = y-1$

dus inderdaad de lineaire vorm

$y = x - 1$.

Ook voor de andere twee Voronoikrommen gaat het op dezelfde manier: per interval moet bekeken worden of het een parabolisch dan wel lineair deel is. Uiteindelijk krijgen we de volgende figuur:

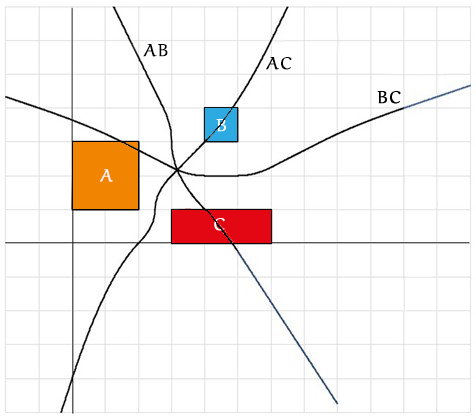
Opgave 3

De drie Voronoikrommen $AB$, $AC$ en $BC$ gaan door één punt, bepaald door hun drie respectievelijke vormen in die ‘buurt’:

$AB:$        $y=3-2\sqrt{x-3}$
$AC:$        $y=x-1$
$BC:$        $y=\tfrac{1}{2}x^2-2x+6$

Deze vergelijkingen twee-aan-twee snijden levert het equidistante punt $(6-2\sqrt{2}, 5-2\sqrt{2})\approx (3{,}17; 2{,}17)$ op. De uiteindelijke Voronoigebieden zijn getekend in de figuur hieronder. De Voronoikrommen zijn afwisselend parabolisch en lineair, maar uiteindelijk (‘ver genoeg weg’) lineair.