Oplossingen Pythagoras Olympiade 58-4, februari 2019

Opgave 397 [oOO]

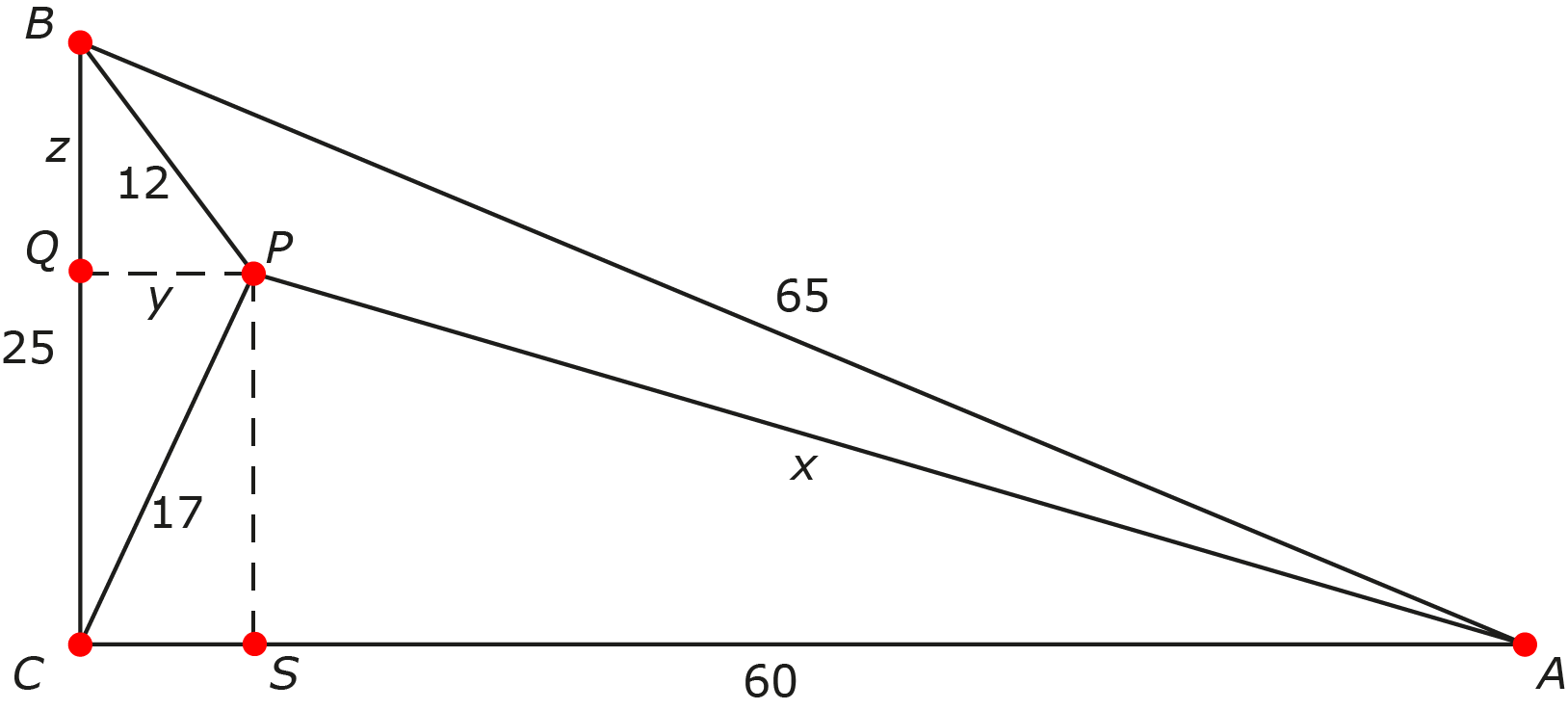
Laat $Q$ het snijpunt zijn van lijnstuk $BC$ met de hoogtelijn in driehoek $BCP$ door het punt $P.$ We zetten de lengte van $BQ$ gelijk aan $y$ en de lengte van $PQ$ gelijk aan $z,$ zodat uit de stelling van Pythagoras in driehoek $BQP$ volgt dat $y^2 + z^2 = 12^2.$ Evenzo geeft de stelling van Pythagoras in driehoek $CPQ$ dat $(25 - y)^2 + z^2 = 17^2.$ Het verschil van deze twee vergelijkingen geeft $-50y = 17^2 - 12^2 - 625 = -480,$ en dus $y = 9{,}6.$ Uit elk van de twee vergelijkingen volgt nu dat $z = 7{,}2.$ Laat verder $S$ het snijpunt zijn van lijnstuk $AC$ met de hoogtelijn in driehoek $ACP$ door het punt $P.$ De stelling van Pythagoras in driehoek $APS$ geeft dat $(25 - y)^2 + (60 - z)^2 = x^2,$ en invullen van de gevonden waardes voor $y$ en $z$ geeft tenslotte $x = 55.$

Opgave 398 [oOO]

We overdekken de groene hokjes in het figuur met een schaakbordpatroon. Door de manier waarop een slang gevormd wordt, bestaat hij uit maximaal één wit blokje meer dan dat hij uit zwarte bestaat (en vice versa.). We tellen $24$ zwarte hokjes, waardoor de slang dus maximaal een lengte van $24 + 24 + 1 = 49$ kan hebben. In het voorbeeld is een slang getekend die ook inderdaad precies lengte $49$ heeft (merk op dat hij alle zwarte hokjes aandoet). Dit is dus de maximale lengte van een slang.

Opgave 399 [ooO]

De grote wijzer gaat met $30^\circ$ per minuut, en gaat dus helemaal rond in precies $360/30 = 12$ minuten. In de derde kwart van elke ronde zit hij in het grijze gebied, wat dus plaatsvindt tussen 6 en $9$ minuten na de start, tussen $18$ en $21$ minuten, enzovoorts. De kleine wijzer gaat met $30^\circ$ per minuut, en doorloopt een ronde dus in $8$ minuten. Deze wijzer zit daarom in het grijze gebied tussen $4$ en $6$ minuten na de start, tussen $12$ en $14$ minuten, tussen $20$ en $22$ minuten, enzovoorts. Tenslotte doorloopt de secondewijzer de klok in $6$ minuten, en is hij dus te vinden in het grijze gebied tussen minuut $1{,}5$ en $3; 7{,}5$ en $9; 13{,}5$ en $15; 19{,}5$ en $21,$ enzovoorts. Vergelijken we deze intervallen, dan vinden we dat de wijzers voor het eerst alle drie in het grijze gebied zijn na $20$ minuten.

Opgave 400 [ooO]

We kijken eerst naar de verwachtingswaarde van het aantal stappen dat Alex naar voren gaat in één beurt. Als Bianca een rode knikker had gepakt, dan is de verwachte waarde van het aantal stappen van Alex gelijk aan

$$\frac12\cdot 1+\frac12\cdot\frac12\cdot 2+\frac12\cdot\frac12\cdot\frac12\cdot 3 + \cdots$$

Een berekening of een schatting laat zien dat dit getal gelijk is aan $2.$ We vinden dezelfde waarde als Bianca een witte knikker had gepakt. Aangezien de kans dat Bianca een rode knikker pakt gelijk is aan $\frac34$ en de kans dat ze een witte knikker pakt gelijk is aan $\frac14,$ vinden we voor Alex een verwacht aantal stappen per beurt gelijk aan $\frac34\cdot 2 + \frac14\cdot 2=2.$ Vervolgens kijken we naar de verwachtings­waarde van het aantal stappen dat Bianca naar voren gaat in één beurt. Als Alex een witte knikker had gepakt, dan is dit verwachte aantal stappen gelijk aan

$$\frac14\cdot 1+\frac34\cdot\frac14\cdot 2+\frac34\cdot\frac34\cdot\frac14\cdot 3+\cdots=4.$$

Als Alex een rode knikker had gepakt, dan is het gelijk aan

$$\frac34\cdot 1+\frac14\cdot\frac34\cdot 2+\frac14\cdot\frac14\cdot\frac34\cdot 3+\cdots=\frac43.$$

Tezamen geeft dit een verwachtingswaarde van $\frac12\cdot 4+\frac12\cdot\frac43=\frac83.$ Aangezien $\frac83\gt 2=\frac63,$ verwachten we dat Bianca vaker wint dan Alex.