Opgave 409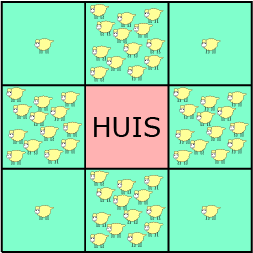

Het was niet helemaal duidelijk, maar bedoeld werd dat het huis in het midden aan alle zijden één raam heeft. Met $H$ geven we het aantal schapen in een stal in een hoek aan. Met $M$ geven we het aantal schapen in een stal in het midden aan (pal voor een raam). Er moet gaan gelden, nadat er $16$ schapen bij gekomen zijn, dat $ 4H + 4M = 56$ terwijl ook $2H + M = 15$, het aantal schapen dat zichtbaar is vanuit een raam. Trek de tweede vergelijking tweemaal af van de eerste vergelijking. Dan vinden we dat $ 2M = 26$, ofwel $M = 13$, waaruit volgt $H = 1$.

 

Opgave 410

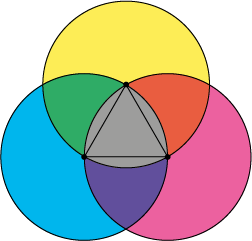
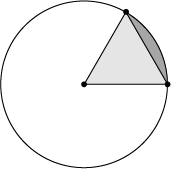
We zoeken in de linkerfiguur de oppervlakte van het grijze deel. Dit deel is uitgelicht in de rechterfiguur. Het licht- en donkergrijs gearceerde deel daarvan is samen $1/6$ van de oppervlakte van een cirkel, $\frac\pi 6$. Het lichtgrijze deel is een gelijkzijdige driehoek met zijde $1$. De oppervlakte is $\frac{\sqrt3}4$. Derhalve is de oppervlakte van het donkergrijze deel

$$\frac{\pi}{6}-\frac{\sqrt3}{4}=\frac{1}{12}(2\pi-3\sqrt3).$$

De gevraagde oppervlak bestaat uit drie donkergrijze delen en een lichtgrijs deel, dus het gevraagde oppervlak is

$$\frac{3}{12}(2\pi-3\sqrt3)+\frac{\sqrt3}{4}=\frac12(\pi-\sqrt3).$$

PS: Het grijze deel in de linkerfiguur heet ook Reuleaux-driehoek. Het getal $\frac12(\pi-\sqrt3)$ heet de constante van Reuleaux.

Opgave 411

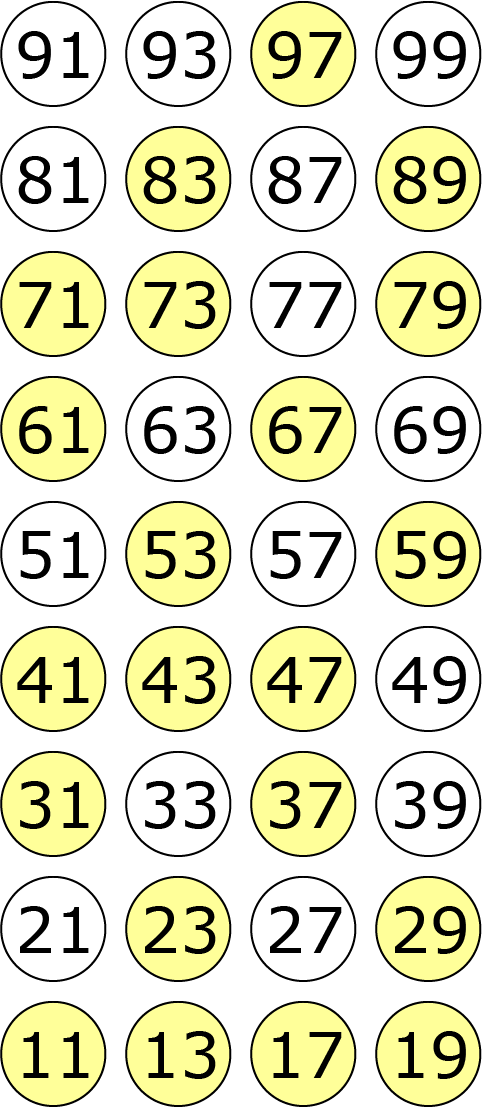
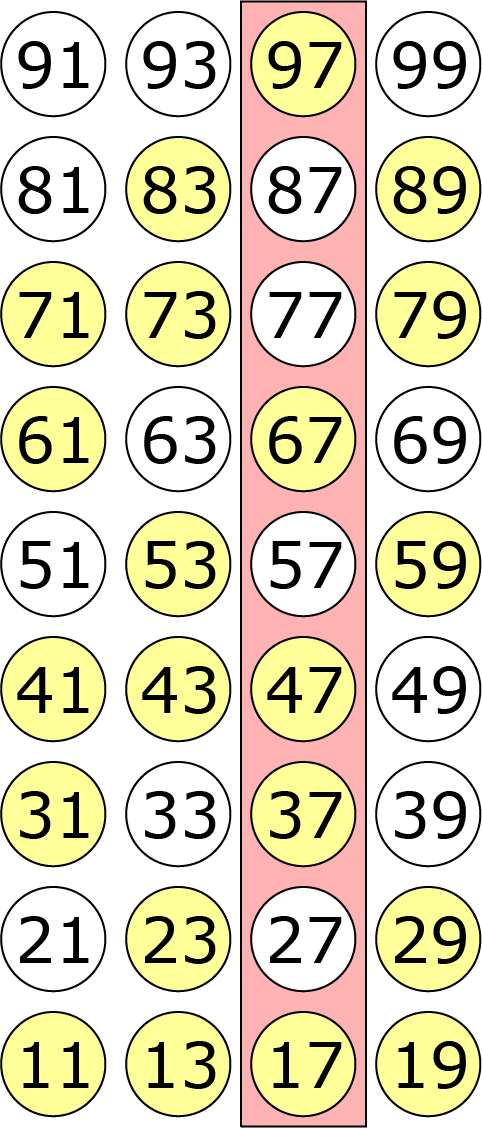
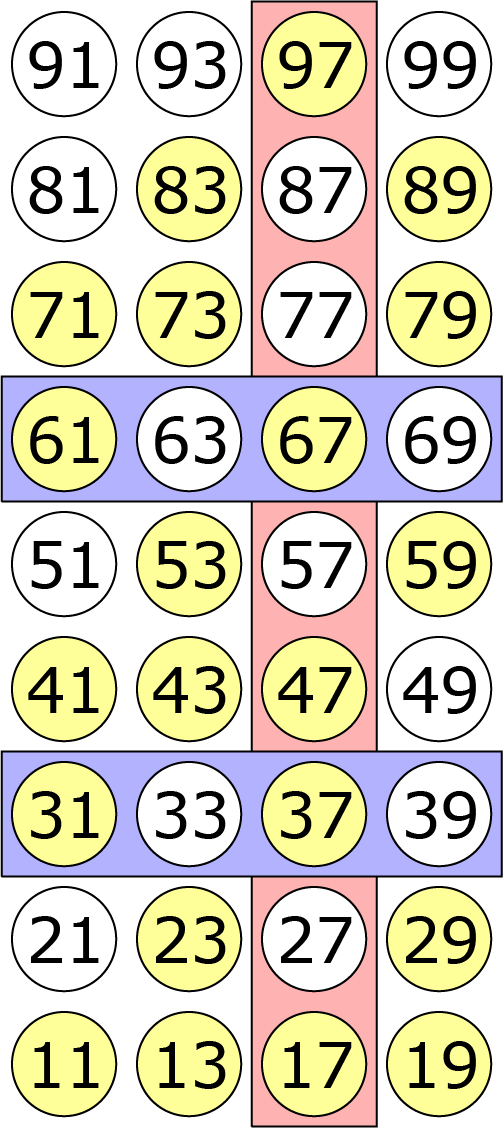
We schrijven alle priemgetallen in een rechthoek, zo dat alle priemgetallen met gelijke eerste cijfers naast elkaar staan en priemgetallen met gelijke laatste cijfers onder elkaar staan. (Zie de getallen die geel zijn gemarkeerd in figuur A) Uit de uitspraak van Erik “Ik weet het

niet” kunnen we afleiden dat Erik niet als eerste getal $9$ heeft gekregen van Maarten. Anders zou Erik het immers wel degelijk hebben geweten. Vervolgens zegt Laura: “Ik weet het ook niet”. Dat hadden we ook zelf kunnen bedenken. Bij elk eerste cijfer zijn meerdere priemgetallen. De andere uitspraak van Laura is echter wel interessant: “trouwens ik wist al dat jij het niet zou weten”. Dat betekent in ieder geval dat Laura geen $7$ als laatste cijfer heeft. We kunnen alle priemgetallen met laatste cijfer schrappen (Zie figuur B) Nu zegt Erik: “Maar nu weet ik wel welk priemgetal Maarten heeft gekozen”. Erik heeft op grond van de uitspraak van Laura kunnen afleiden dat $7$ niet het laatste cijfer is. In het geval dat Erik een $3$ of een $6$ heeft zijn er twee mogelijkheden, waarbij de tweede mogelijkheid eindigt op een $7$. Erik heeft derhalve de andere mogelijkheid ($31 $ of $61$), zie figuur C. Laura heeft als laatste cijfer een $1$, maar kan niet achterhalen om welk priemgetal het gaat.

Opgave 412

We noemen de kansen dat de euro onder een bekertje ligt respectievelijk $L, M$ en $R, $ voor de bekertjes links, midden en rechts. Er geldt dat $L + M + R = 1$. We geven nu de opeenvolgende kansen weer met Ln, Mn en Rn, waarbij $n$ varieert van $0$ tot en met $100. $ Het eerste wat we doen is $L_{n+1}, M_{n+1}$ en $R_{n+1} $ uitdrukken in Ln, Mn en Rn. Voor links en rechts geldt dat met $50\%$ kans de euro onder het bekertje blijft (als Kees de middelste beker wisselt met de andere beker) en met $50\%$ kans verdwijnt naar de middelste beker. Voor de middelste beker geldt dat de euro sowieso verdwijnt en wel met een kans van $50\%$ naar links en $50\% $ naar rechts. In formulevorm:

$$\left\{
\begin{array}{rcl}
L_{n+1}&=&\frac12(L_n+M_n)\\
M_{n+1}&=&\frac12(L_n+R_n)\\
R_{n+1}&=&\frac12(M_n+R_n)
\end{array}\right..$$

We zijn niet geïnteresseerd in de bekertjes rechts en links afzonderlijk, maar in de som (we noteren $S = L + R$).

$$\left\{\begin{array}{rcl}
S_{n+1}&=&\frac{S_n}{2}+M_n\\
M_{n+1}&=&\frac{S_n}{2}
\end{array}\right..$$

Op den duur zal onder ieder van de bekertjes met een kans van een derde een euro liggen. Maar er blijft een afwijking. We kijken nu naar deze afwijking. We schrijven $L_n = \frac13 + l_n$, $M_n = \frac13 + m_n$ en $R_n = \frac13 + r_n$ en dus $S_n = \frac23 + s_n$. Voor de afwijkingen $s_n$ en $m_n$ geldt $s_n + m_n = 0$ (ofwel $s_n = -m_n$). We kunnen net als de kansen voor de afwijkingen van een derde een expressie opstellen van na en voor het wisselen van bekers:

$$\left\{\begin{array}{rcl}
s_{n+1}&=&\frac12s_n+m_n=\frac12m_n\\
m_{n+1}&=&\frac12s_n=-\frac12m_n
\end{array}\right..$$

en evenzo twee wisselingen:

$$\left\{\begin{array}{rcl}
s_{n+2}&=&-\frac14m_n\\
m_{n+2}&=&\frac14m_n
\end{array}\right..$$

We zien dat in het midden de kans op een euro wisselend groter (even) en kleiner (oneven) dan een derde zal zijn.

Na 100 wisselingen is de kans groter dan een derde.
Dit verschil is echter slechts $\frac23(\frac12)^{100}$.