Opgave 497 ^[oOO]

We noemen het getal dat Peter in zijn hoofd heeft even $x$. Dan is $x - 13$ een kwadraat, dus we kunnen schrijven $x - 13 = m^2$ met $m$ een positief geheel getal (merk op dat $m = 0$ niet kan omdat dan $x = 13$, en dat heeft geen drie cijfers). Ook is $x + 32$ een kwadraat, dus $x + 32 = n^2$. Dan geldt dus $n^2 - m^2 = (x + 32) - (x - 13) = 45$, oftewel $(n + m)(n - m) = 45$. Omdat $n + m > n - m$ hebben we twee mogelijkheden: 

1. $n + m = 9$ en $n - m = 5$. In dit geval is $n = 7$ en $m = 2$, en vinden we $x = m^2 + 13 = 17$. Dit heeft geen drie cijfers, dus het is geen oplossing. 
2. $n + m = 15$ en $n - m = 3$. In dit geval is $n = 9$ en $m = 6$, en vinden we $x = m^2 + 13 = 49$. Dit heeft ook geen drie cijfers, dus het is ook geen oplossing. 
3. $n + m = 45$ en $n - m = 1$. In dit geval is $n = 23$ en $m = 22$, dus $x = m^2 + 13 = 497$. Dit heeft wel drie cijfers en is inderdaad een oplossing, want $x - 13 = 484 = 22^2$ en $x + 32 = 529 = 23^2$. 

We hebben maar een oplossing gevonden, namelijk $497$, dus dat moet het getal zijn waar Peter aan dacht.

Opgave 498 ^[oOO]

Met twee dobbelstenen is de kans dat we geen $1$ gooien gelijk aan $\frac{5}{6} \cdot \frac{5}{6} = \frac{25}{36}$. De kans op minstens een $1$ is dus gelijk aan $1 - \frac{25}{36} = \frac{11}{36}$. Elke keer dat we met twee dobbelstenen gooien is er dus een kans van $\frac{11}{36}$ op minstens een $1$. We willen nu weten hoeveel worpen er dan nodig zijn tot we tenminste een $1$ gooien. Als we met slechts een dobbelsteen gooien is de kans op een $1$ gelijk aan $\frac{1}{6}$ en duurt het gemiddeld $6 = \left(\frac{1}{6}\right)^{-1}$ keer. Het ligt dan ook voor de hand dat het verwachte aantal worpen tot we tenminste een $1$ gooien gelijk is aan $\left(\frac{11}{36}\right)^{-1} = \frac{36}{11} = 3\frac{3}{11}$. 

Om dit te bewijzen: laat $p$ de kans zijn op een 'succes' bij de eerste worp. Laat $T$ het verwachte aantal worpen zijn tot we minstens een succes hebben. Merk op dat als de eerste worp geen succes oplevert, dat de verwachtte tijd daarna nog even lang is, omdat alle worpen onafhankelijk zijn. We hebben dus
$$T = p \cdot 1 + (1 - p) \cdot (T + 1).$$
en als we dit oplossen vinden we $T = \frac{1}{p}$. We concluderen dus dat het verwachte aantal worpen inderdaad gelijk is aan $\frac{36}{11}$. 

Opgave 499 ^[ooO]

Het antwoord is nee, zo'n drietal bestaat niet. Dit bewijzen we uit het ongerijmde. Laat $(a, b, c)$ zo'n drietal zijn. Merk op dat $kgv(a, b)$ deelbaar is door $a$ en $b$ (per definitie). Ook is $kgv(a, b) = kgv(b, c) - kgv(a, c)$, en omdat de rechterkant deelbaar is door $c$ is $kgv(a, b)$ ook deelbaar door $c$. Dus geldt dat $kgv(a, b)$ deelbaar is door $a, b$ en $c$, en dus ook door $kgv(a, b, c)$. Maar omdat $kgv(a, b)$ duidelijk een deler is van $kgv(a, b, c)$, geldt dus $kgv(a, b) = kgv(a, b, c)$ (omdat beide getallen positief zijn). Op dezelfde manier kunnen we bewijzen dat $kgv(a, c) = kgv(a, b, c)$ en $kgv(b, c) = kgv(a, b, c)$. Maar dan kunnen we
$$kgv(a, b) + kgv(a, c) = kgv(b, c)$$
ook schrijven als
$$kgv(a, b, c) + kgv(a, b, c) = kgv(a, b, c)$$
oftewel $kgv(a, b, c) = 0$, wat natuurlijk niet kan omdat een $kgv$ altijd positief is. We concluderen dat zo'n drietal $(a, b, c)$ niet bestaat. 

Opgave 500 ^[ooO]

De eerste stap is constateren dat een bouwset precies 225 $1 \times 1 \times 1$ kubusjes bevat. Met twee bouwsets hebben we dus $450$ kubusjes. We moeten dus een aantal blokken uit de derde set kiezen met precies $50$ kubusjes. De blokjes in een set bestaan uit (gesorteerd van klein naar groot)  $6$, $8$, $10$, $12$, $15$, $20$, $24$, $30$, $40$ en $60$ kubusjes. We kiezen het blok met $60$ kubusjes sowieso niet, dan hebben we er meteen al te veel. Voor de rest kunnen we gevalsonderscheiding gebruiken:

• Het grootste blok is de $40$. Dan is de enige manier om tot een som van $50$ te komen om ook het blok van $10$ te nemen. 
• Het grootste blok is de $30$. Dan kunnen we ofwel de $20$ nemen, ofwel de $8$ en de $12$. 
• Het grootste blok is de $24$. Dan kunnen we ofwel de $20$ en de $6$, ofwel de $12$, $8$ en $6$ nemen.
• Het grootste blok is de $20$. Dan komen we alleen uit door de $12$, $10$ en $8$ te nemen. 

We vinden dus 6 mogelijke oplossingen: we willen nu nog wel bewijzen dat dit ook allemaal daadwerkelijke oplossingen zijn. We moeten sowieso een oplossing vinden voor het $40 + 10$ en het $30 + 20$ geval. De rest van de gevallen kunnen we dan direct hieruit construeren, als volgt:

• Indien we de $30$, $8$ en $12$ hebben, voegen we de $8$ ($1 \times 2 \times 4$) en de $12$ ($1 \times 3 \times 4$) samen tot een $20$ ($1 \times 4 \times 5$) blok. 
• Indien we een $24$, $20$ en $6$ hebben, kunnen we de $24$ ($2 \times 3 \times 4$) en de $6$ ($1 \times 2 \times 3$) samenvoegen tot een $30$ ($2 \times 3 \times 5$) blok. 
• Indien we een $24$, $12$, $8$ en $6$ hebben, kunnen we de $8$ en $12$ samenvoegen, en de $6$ en $24$ net zoals hierboven beschreven.
• Indien we een $20$, $12$, $10$ en $8$ hebben, kunnen we de $8$ en $12$ samenvoegen tot een $20$ ($1 \times 4 \times 5$), en die dan samen met de andere $20$ (ook $1 \times 4 \times 5$) tot een $40$ ($2 \times 4 \times 5$)

Dus als we een oplossing kunnen vinden voor de gevallen dat we een $40$ en een $10$ blok toevoegen, en voor het geval dat we een $30$ en een $20$ blok, dan zijn we klaar. 

Om het nog wat simpeler te maken, kunnen we van beide complete sets de $6$ en $24$ blokken samenvoegen tot een $30$ blok, en de $8$ en $12$ blokken tot een $20$ blok. Nu heeft ieder blok tenminste een zijde van $5$. Als we al die zijden verticaal plaatsen dan moeten we nu een $10\times 10$ vierkant vullen met een aantal rechthoeken. Een tabel van hoeveel:

Rechthoek	$1\times 2$	$1\times 3$	$1\times 4$	$2\times 3$	$2\times 4$	$3\times 4$
$30+20$	$2$	$2$	$5$	$5$	$2$	$2$
$40+10$	$3$	$2$	$4$	$4$	$3$	$2$

Een oplossing voor $30 + 20$ resp. $40 + 10$ wordt hieronder gegeven. 

    

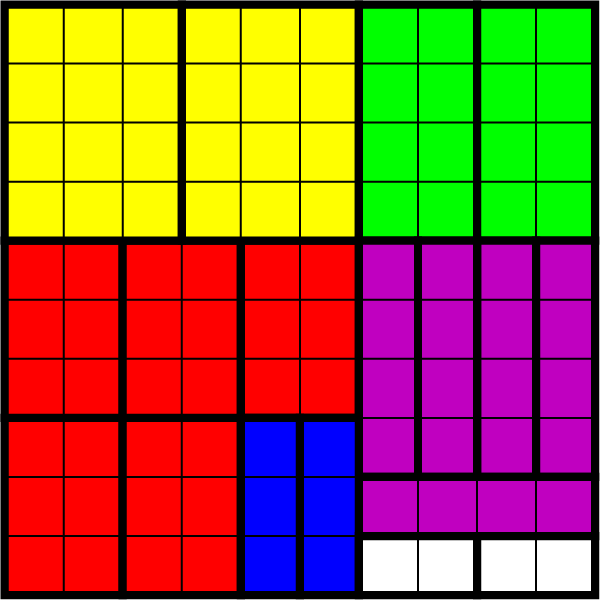
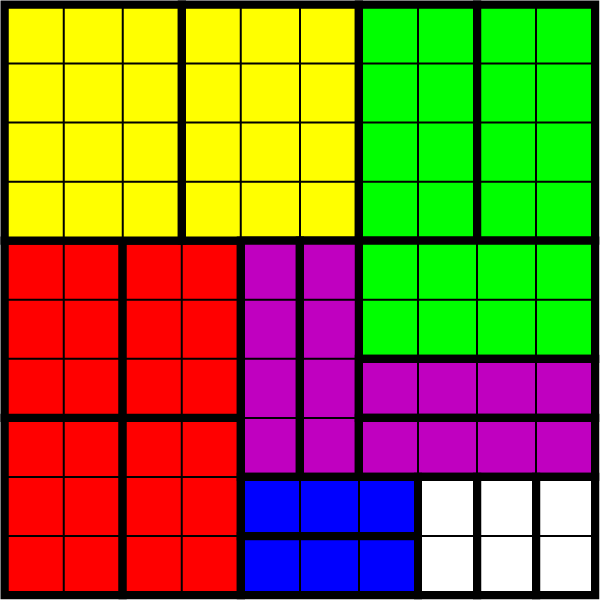
Er zijn nog veel meer oplossingen te bedenken natuurlijk, maar een is voldoende om te laten zien dat het mogelijk is.