Opgave 545 ^[oOO]

Iemand van generatie $n$ wordt $n$ jaar oud in het jaar $n^2$, en is daarom geboren in het jaar $n^2 - n$. De volgende generatie $n+1$ is dan geboren in het jaar $(n+1)^2 - (n+1) = n^2 + 2n + 1 - n - 1 = n^2 + n$. Als er precies 90 jaar tussen deze twee geboortejaren moet zitten, dan volgt $2n = 90$ en dus $n = 45$. De mensen van generatie 45 vieren hun speciale verjaardag in het jaar $45^2 = 2025$ - dit jaar dus! 

Opgave 546 ^[oOO]

Een getal dat bestaat uit een even aantal negens is deelbaar door $11$, omdat het gelijk is aan

$$99 \ldots 99 = 9 \cdot 11 \ldots 11 = 9 \cdot 11 \cdot 1010 \ldots 1010.$$

Als we $2$ optellen bij zo'n getal met een even aantal negens, dan is het enerzijds niet langer deelbaar door $11$, en anderzijds gelijk aan $10\ldots 01$ met een oneven aantal nullen - dit getal is dus nooit deelbaar door $11$. Als we zo'n getal met een even aantal negens vermenigvuldigen met $10$ en er dan $11$ bij optellen, dan blijft het deelbaar door $11$. Anderszijds is het gelijk aan $10 \ldots 01$ met een even aantal nullen - dit getal is dus altijd deelbaar door $11$.

Opgave 547 ^[ooO]

De twee gezochte oplossingen zijn

$$(30+25)^2 = 3025 \quad \text{and} \quad (98+01)^2 = 9801.$$

Dit kan met een brute force zoektocht gedaan worden, maar het is ook mogelijk om met enkele slimmigheden de zoektocht te beperken naar iets wat men binnen enkele minuten met de hand kan uitwerken. Laat daartoe $x$ de eerste twee cijfers van het getal voorstellen, en $y$ de laatste twee. We zoeken dan oplossingen van de vergelijking $(x+y)^2 = 100x + y$, wat we kunnen herschrijven tot $x^2 + (2y-100)x + (y^2 - y) = 0$. De discriminant van deze kwadratische vergelijking is gelijk aan 

$$(2y-100)^2 - 4(y^2-y) = 4y^2 - 400y + 10000 - 4y^2 + 4y = 10000 - 396y = 4( 2500 - 99y ).$$

We zien in het bijzonder dat $2500 - 99 y \ge 0$, waaruit volgt dat $y \le 25$. Men gaat nu eenvoudig met de hand na dat $2500 - 99y$ enkel een kwadraat is voor $y = 0$, $y = 1$ en $y = 25$, waaruit de oplossingen vlug volgen.

Opgave 548 ^[ooO]

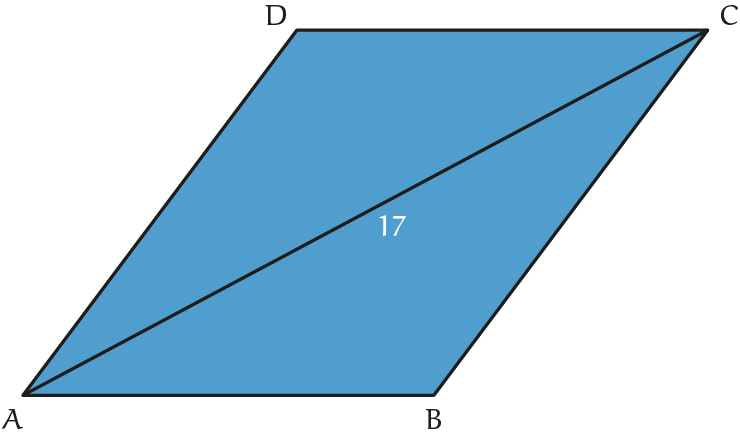
Laat voor het gemak $|AB| = a$ en $|BC| = b$. Omdat $ABCD$ omtrek 38 heeft, volgt dat $2a+2b = 38$ en zo $a+b = 19$. We gebruiken nu de formule van Heron voor driehoek $ABC$, met een oppervlakte van $72 / 2 = 36$ en tevens een omtrek van $19+17 = 36$. We vinden dat

$$36^2 = 18 \cdot (18 - 17) \cdot (18-a) \cdot (18 - b).$$

Dit is om te schrijven tot

$$72 = (18 - a)(18-b) = 324 - 18(a+b) + ab = 18^2 - 18 \cdot 19 + ab = -18 + ab.$$

We vinden dat $ab = 90$ en samen met $a+b = 19$ volgt dat $\{ a,b \} = \{ 9, 10 \}$. De parallellogramidentiteit geeft dan dat

$$|BD|^2 + 17^2 = 2(a^2+b^2) \implies |BD|^2 = 2(9^2+10^2) - 17^2 = 73.$$

We concluderen dat $|BD| = \sqrt{73}$.