Ellipsen zijn zonder twijfel de bekendste ovalen. Ze komen voor als kegelsneden en als planetenbanen. Een ellips kan worden gezien als een cirkel die in één richting is ingedrukt of uitgerekt. Alle punten ervan hebben dezelfde som van afstanden tot twee vaste punten, de brandpunten van de ellips. Daarom kun je een ellips tekenen door twee punaises (de brandpunten) door het papier te drukken, er een lus van draad omheen te leggen en een potlood binnen die lus de wijdst mogelijke baan rondom de punaises over het papier te laten afleggen. Een ellips kan in elk punt worden benaderd met een cirkel, maar omdat die cirkel overal weer anders is, bestaat een ellips niet uit stukjes cirkelboog. Toch worden cirkelbogen veel gebruikt om ellipsen zo goed mogelijk te benaderen. Het tekenen van cirkelbogen is immers nog gemakkelijker dan het tekenen van een ellips.

Om ellips-benaderingen of ellips-achtige krommen met stukjes cirkelboog te tekenen volstaat het een kwart te beschouwen. Figuur 1 toont de eenvoudigste constructie: een kwart ovaal binnen een rechthoek $OADB$ opgebouwd met twee cirkelsectoren of 'taartpunten', in $\color{red}{rood}$ en in $\color{purple}{paars}$, met stralen van verschillende lengte, die tegen elkaar aan liggen. De punten $C_1 = (c_1, 0)$ en $C_2 = (0, -c_2)$ van de sectoren heten de centra van het ovaal. Het zijn de middelpunten van de cirkels waar de bogen deel van uitmaken. Het punt $T$ waar de bogen op elkaar aansluiten heet het verbindings- of overgangspunt. De bogen sluiten glad, dat wil zeggen zonder knik op elkaar aan. De redenering is als volgt. In het algemeen geldt dat een raaklijn aan een cirkel loodrecht staat op de straal tussen raakpunt en middelpunt. In het overgangspunt geldt dit voor de raaklijnen aan elk van beide cirkelbogen. Omdat de stralen tussen het overgangspunt en elk van beide centra samenvallen, hebben de bogen in het overgangspunt een gemeenschappelijke raaklijn. Het ovaal dat ontstaat door te spiegelen in beide assen bestaat uit vier cirkelbogen en heeft vier centra; vanwege symmetrie sluiten de kwarten op elkaar aan met bogen van dezelfde cirkel.

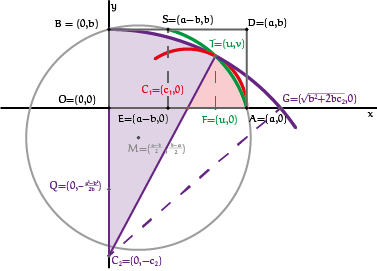
Gegeven de lengten $a$ en $b (0 < b < a)$ van de halve assen kunnen verschillende, in feite oneindig veel, tweetallen cirkelsectoren worden ingetekend. Wie dit probeert zal echter zien dat niet elke willekeurige keuze van $0 < c_1 < a$ en $c_2 > 0$ zomaar een goede, dat wil zeggen gladde ovaal oplevert. Welke keuzen wel? Zorgvuldige beschouwing van figuur 1 leert dat er de volgende onderlinge afhankelijkheden zijn:

• De cirkelsectoren moeten netjes tegen elkaar aan liggen opdat hun bogen glad aansluiten. Dit komt erop neer dat de centra $C_1$ en $C_2$ en het overgangspunt $T$ op één lijn moeten liggen, zodat de stralen van de cirkels op één lijn liggen en de raaklijnen in $T$, die loodrecht op de stralen staan, samenvallen. Langs deze lijn hebben de lengten van de stralen het volgende verband (lees de lengten van de stralen af en pas de stelling van Pythagoras toe op de driehoek $OC_1C_2$):
  $$b+c_2=\sqrt{c_1^2+c_2^2}+a-c_1.\hspace{4em}\color{purple}{(\ast)}$$
• De rechter, $\color{red}{rode}$ cirkelsector mag niet boven de rechthoek uitsteken, dus de straal ter lengte $a - c_1$ moet korter zijn dan de hoogte $b$ van de rechthoek, ofwel $a - b < c_1 < a$. Het centrum $C_1$ ligt dus altijd tussen de punten $E = (a - b, 0)$ en $A = (a, 0)$.
• De linker, $\color{purple}{paarse}$ cirkelsector moet zo groot zijn dat het snijpunt $G=\left(\sqrt{b^2+2bc_2},0\right)$ van de doorgetrokken cirkelboog en de $x$-as rechts van het punt $A$ ligt (pas de stelling van Pythagoras toe op de driehoek $OC_2G$ en merk op dat de schuine zijde $C_2G$ even lang is als de straal $C_2B$). Er volgt $\frac{a^2-b^2}{2b}<c_2<\infty$. Het centrum $C_2$ ligt dus altijd onder het punt $Q =\left(0, -\frac{a^2-b^2}{2b}\right)$.
• De vergelijking $(\color{purple}{\ast})$ is te herschrijven tot een vorm die aan het licht brengt dat het punt $(c_1, c_2)$ op een hyperbool ligt met asymptoten $x = a - b$ en $y = a - b$:
  $$(c_1 - (a - b))(c_2 - (a - b)) = \tfrac{1}{2}(a - b)^2.\hspace{4em}\color{purple}{(\ast\ast)}$$

(Reken na dat $\color{purple}{(\ast\ast)}$ en het kwadraat van $\color{purple}{(\ast)}$ overeenkomen en teken de hyperbool in het $c_1c_2$-vlak.) Het voordeel van deze voorstelling is dat je de samenhang tussen de grenzen van $c_1$ en $c_2$ ziet: uit $a - b < c_1 < a$ volgt $\frac{a^2-b^2}{2b}<c_2<\infty$ en omgekeerd.

Is naast $a$ en $b$ één van de parameters $c_1$ of $c_2$ gegeven of gekozen, binnen de genoemde grenzen, dan volgt de andere uit $\color{purple}{(\ast)}$.

Nu wordt het tijd het overgangspunt $T = (u, v)$ te bepalen. Uit figuur 1 blijkt dat de driehoeken $OC_1C_2$ en $FC_1T$ gelijkvormig zijn, dus hun verhoudingen tussen overeenkomende zijden zijn gelijk: 

• Korte rechthoekszijde gedeeld door schuine zijde: $\frac{c_1}{\sqrt{c_1^2+c_2^2}}=\frac{u-c_1}{a-c_1}$.
• Lange rechthoekszijde gedeeld door schuine zijde: $\frac{c_2}{\sqrt{c_1^2+c_2^2}}=\frac{v}{a-c_1}$.

Hieruit volgen direct u en v, en met gebruik van $\color{purple}{(\ast)}$ vind je dan:

$$T=(u,v)=\left(\frac{c_1(b+c_2)}{-a+b+c_1+c_2},\frac{c_2(a-c_1)}{-a+b+c_1+c_2}\right).\hspace{4em}\color{purple}{(\ast\ast\ast)}$$

Een volgende vraag dringt zich op. Welke punten in het vlak kan het overgangspunt innemen? Er is een mooie stelling over de ligging ervan (in All Sides to an Oval toegeschreven aan Felice Ragazzo):

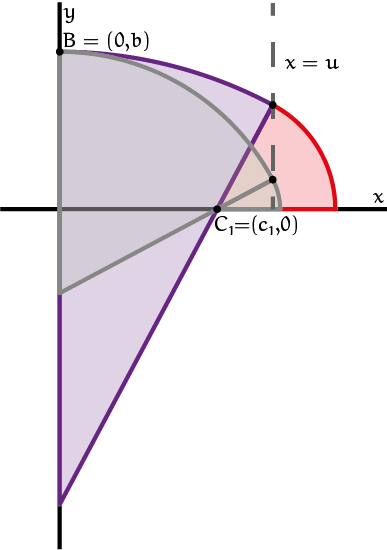
De overgangspunten $T$ van een ovaal uit twee cirkelsectoren met halve assen $OA$ en $OB$ zijn precies de punten die liggen op de verbindings- of overgangsboog $AS$, in $\color{green}{groen}$. Dit is de boog die deel uitmaakt van de cirkel die wordt bepaald door de drie punten $A$, $B$ en $S$, waarbij $S = (a - b, b)$ het punt op het lijnstuk $BD$ is waarvoor de lijnstukken $SD$ en $AD$ even lang zijn. Deze cirkel heeft middelpunt $M=\left(\frac{a-b}{2},\frac{b-a}{2}\right)$ en straal $R=\sqrt{\frac{a^2+b^2}{2}}$. Kortom, $A$, $B$, $S$ en $T$ liggen op dezelfde afstand $R$ van $M$ (reken dit na ter bewijs van de stelling).

De punten op de overgangsboog zijn precies de punten waar de cirkelbogen glad aansluiten. Van een gegeven ovaal is het overgangspunt het snijpunt met de overgangsboog. Omgekeerd kan elk punt op de overgangsboog dienen als overgangspunt van een of andere kwart ovaal ingeschreven in de rechthoek. De afbeelding $T = (c_1, c_2)$ bestrijkt voor de mogelijke waarden van $c_1$ en $c_2$ de gehele boog $AS$ (zonder de uiterste punten $A$ en $S$).

Als $T$ naar $S$ gaat, en dus $c_1 \rightarrow a - b$ en $c_2 \rightarrow \infty$, dan wordt het $\color{purple}{paarse}$ stuk een onbegrensde verticale strook met het lijnstuk $B$S als bovenzijde, en de $y$-as en de lijn $x = a - b$ als zijkanten. Het $\color{red}{rode}$ stuk wordt een kwart cirkel om $E$ en door $S$ en $A$. Het totale ovaal wordt dan een schaats- of atletiekbaan; dit heet een stadium, twee halve cirkels verbonden door (rechte) lijnstukken.

Als $T$ naar $A$ gaat, en dus $c_1 \rightarrow a$ en $c_2 \rightarrow \frac{1}{2b}\left(a^2 - b^2\right)$, dan verdwijnt het $\color{red}{rode}$ stuk en blijft alleen het $\color{purple}{paarse}$ stuk over, dus één taartpunt met een cirkelboog die $B$ en $A$ verbindt en $Q$ als middelpunt heeft. De totale kromme is niet echt een ovaal meer, want bij $A = (a, 0)$ en $(-a, 0)$ zijn er dan scherpe punten; het is een amandel geworden.

Opgave 1 Experimenteer in Geogebra. Neem een willekeurig punt op de overgangsboog, teken de twee cirkelsectoren en zie dat ze gegarandeerd glad aansluiten. Teken vervolgens voor een punt net buiten de overgangsboog de cirkelboog die in $A$ loodrecht op de $x$-as staat en door dat punt gaat en de cirkelboog die in $B$ loodrecht op de $y$-as staat en door dat punt gaat, en zie dat ze niet glad aansluiten.

Hierboven zijn de zes parameters $a, b, c_1, c_2, u$ en $v$ ten tonele gevoerd. Er is uitgelegd dat als je $a, b, c_1$ of $a, b, c_2$ hebt gekozen, je de andere drie kunt uitrekenen met $\color{purple}{(\ast)}$ en $\color{purple}{(\ast\ast\ast)}$. Ook voor andere keuzen van drie uit het zestal kun je proberen de overige drie op te lossen. In het boek All Sides to an Oval worden alle twintig mogelijke gevallen behandeld. Ze zijn op twee gevallen na opgelost, op één na met een eenduidig bepaald ovaal. In de opgeloste gevallen kunnen passende ovalen worden getekend die aan de gestelde voorwaarden voldoen. Er zijn twee ovalen mogelijk in het geval dat $b$, $c_1$ en $u$ gegeven zijn en binnen zekere grenzen vallen. De $b$, $c_1$ en $u$ in figuur 1 voldoen daaraan. Figuur 2 toont zowel het kwart ovaal van figuur 1 als een kwart van het andere ovaal in grijs. Ze hebben dezelfde $b$, $c_1$ en $u$, maar verschillende $a$, $c_2$ en $v$.

Je kunt de constructie van een kwart ovaal uitvoeren met elk aantal cirkelsectoren (met één is het noodzakelijkerwijs een kwart cirkel). Figuur 3 toont een voorbeeld met drie stuks. Er zijn een centrum en een overgangspunt bijgekomen. De wiskundige beschouwing wordt met toenemend aantal snel omvangrijker.

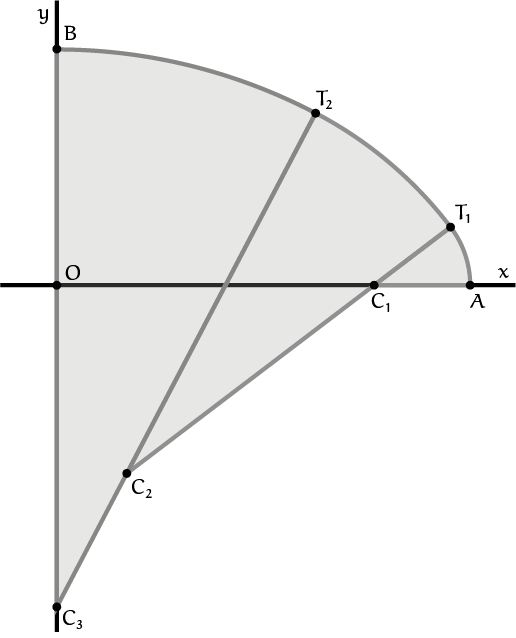
Opgave 2 Experimenteer in Geogebra met drie cirkelsectoren. Je zult merken dat het best even moeite kost ze glad aan elkaar te leggen. Je kunt ook proberen te rekenen aan de verbanden tussen de ligging van de centra en overgangspunten.

In toepassingen zullen er eisen zijn aan de precieze vorm van een ovaal om goed in het totale ontwerp te passen. Dan helpt het als je kunt putten uit ovalen met bekende eigenschappen. Omgekeerd is het bijvoorbeeld interessant te achterhalen welke zijn toegepast in overgebleven bouwwerken uit vroeger tijden, zoals amfitheaters, koepels en bogen. De vraag is dan of metingen aan het bouwwerk passen bij een ovaal van een bekende soort.

Hier is slechts een beperkte selectie ovalen besproken: ellipsen, ovalen van stukjes cirkelboog en stadia. Er zijn zoveel verschillende vormen die ovaal kunnen worden genoemd dat er geen uitputtende opsomming kan worden gegeven. Wel kunnen eigenschappen worden opgesomd die uitmaken of een kromme voor ovaal kan doorgaan. Gangbare punten in een algemene definitie zijn:

• een ovaal is een kromme in het platte vlak die gesloten is en zichzelf niet doorsnijdt,
• een ovaal is convex: voor elk tweetal willekeurige punten op het ovaal ligt hun verbindingslijnstuk volledig op of binnen het ovaal,
• een ovaal is glad, heeft geen knikken: een ovaal heeft in elk punt een eenduidige raaklijn.

Een zijaanzicht van een ei levert dus, gelukkig, ook een ovaal. 

Mazzotti, Angelo Alessandro (2019), All Sides to an Oval – Properties, Parameters  and Borromini’s Mysterious Construction, Second Edition, Springer.