
Pi en leuke oppervlakken
Als je wilt weten hoe groot een boomstam is dan kun je twee dingen doen: met een schuifmaat kan je de doorsnede meten of met een meetlint kan je de omvang meten. Lang voordat je klaar bent met het hele bos opmeten zou opgevallen zijn dat de tweede meting altijd ongeveer drie keer groter is dan de eerste meting.
Vóór de coronatijd kon je nog zes mensen vragen om elkaar bij de hand te pakken en met gestrekte armen een kring te vormen. Als twee andere mensen elkaar met één hand vasthouden, dan zouden ze er met gestrekte armen net in passen. Op zoek naar meer precisie zou je allerlei ronde objecten (bloempotten, deksels, frisbees, etc.) kunnen meten. Touwtje er omheen, markeren en touwtje er doorheen tot de maximale afstand en ook weer markeren. Dan de twee gemarkeerde
afstanden meten met een liniaal en op zoek gaan naar een rekenmachine om de lange afstand er omheen te delen door de korte afstand er doorheen. Je antwoord is nu waarschijnlijk ongeveer $3{,}1$ of zelfs $3{,}14$.
Neem nu afstand van al deze experimenten met ronde objecten in de reële wereld en denk aan een echte perfecte cirkel. Een goed moment om de twee afstanden hun gebruikelijke namen te geven. De lange afstand er omheen noemen we de omtrek en de korte afstand er doorheen noemen we de diameter. De straal is de afstand van het middelpunt tot de rand van een cirkel en is dus de helft van de diameter. Nu is er een precieze waarde voor $\frac{\rm diameter}{\rm omtrek}$. En als we een andere cirkel kiezen dan wordt de vergrotingsfactor voor de omtrek hetzelfde als voor de diameter. Dan blijft dus de waarde van $\frac{\rm diameter}{\rm omtrek}$ hetzelfde. Deze constante waarde voor alle cirkels draagt de naam $\pi$. De waarde van $\pi$ geeft aan hoeveel diameters van een cirkel passen in zijn omtrek.
Op naar de formules. De diameter en straal korten wij af met de letters $d$ en $r$. Nu is van het voorgaande duidelijk dat voor alle cirkels geldt dat ${\rm omtrek} = \pi \cdot d$ en dus ${\rm omtrek} = 2 \cdot \pi \cdot r$.
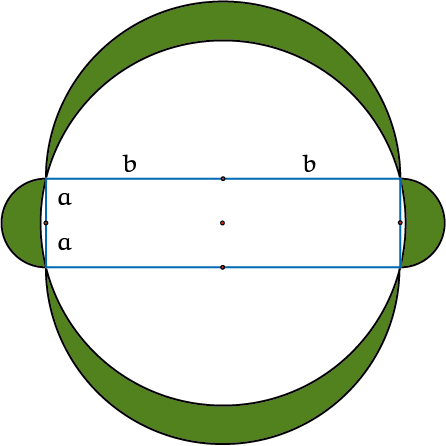
Op het eerste gezicht is het heel merkwaardig dat $\pi$ ook te vinden is in de formule voor de oppervlakte van een cirkel: ${\rm oppervlakte} = \pi \cdot r^2$. Maar als je een cirkel in veel gelijke sectoren snijdt en deze cirkel-stukken om en om
naast elkaar plaatst zie je iets dat op een rechthoek lijkt. Zie figuur 1. Bedenk dat de groene lijnen samen de hele omtrek van de cirkel zijn.
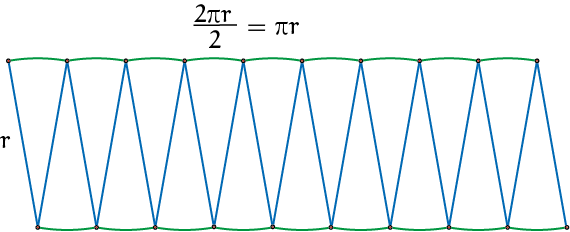
Maar hij leunt een beetje en heeft twee kartelranden. Verder snijden in nog dunnere sectoren helpt om hem beter te laten passen in een rechthoek met ${\rm oppervlakte} = r \cdot \pi r$. Intuïtief vind ik dit een heel overtuigende demonstratie voor
de formule.
Voor diegene die nog twijfels heeft, is er een bewijs te vinden in het feit dat de omtrek van een cirkel de afgeleide moet zijn van zijn oppervlakte als een functie van $r$. Dit verklaart ook waarom de formules hetzelfde zijn met uitzondering van de plaatsing van de $2$. In Pythagoras 57-2 (november 2017) staat een bewijs van Archimedes.
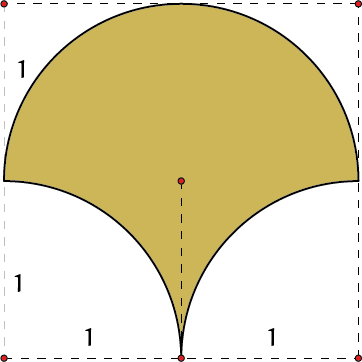
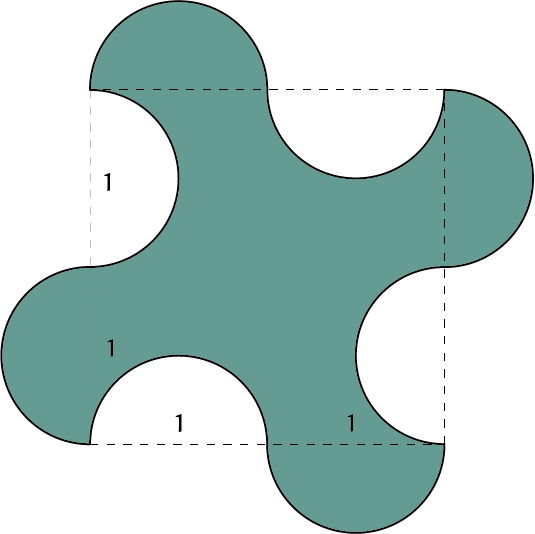
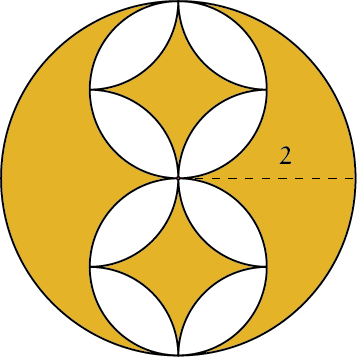
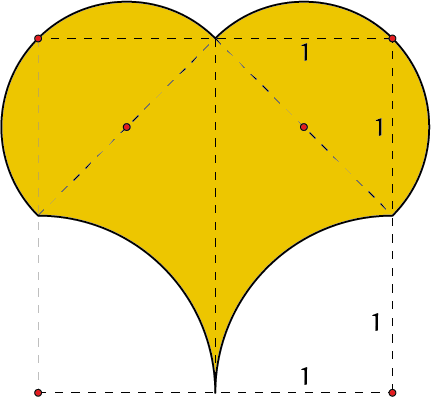
OpgaveDe volgende gekleurde figuren zijn |
|
||
|

|
||

|
|
||
|
|
De antwoorden vind je onder de knop [Bekijk oplossing]
Bekijk oplossing
