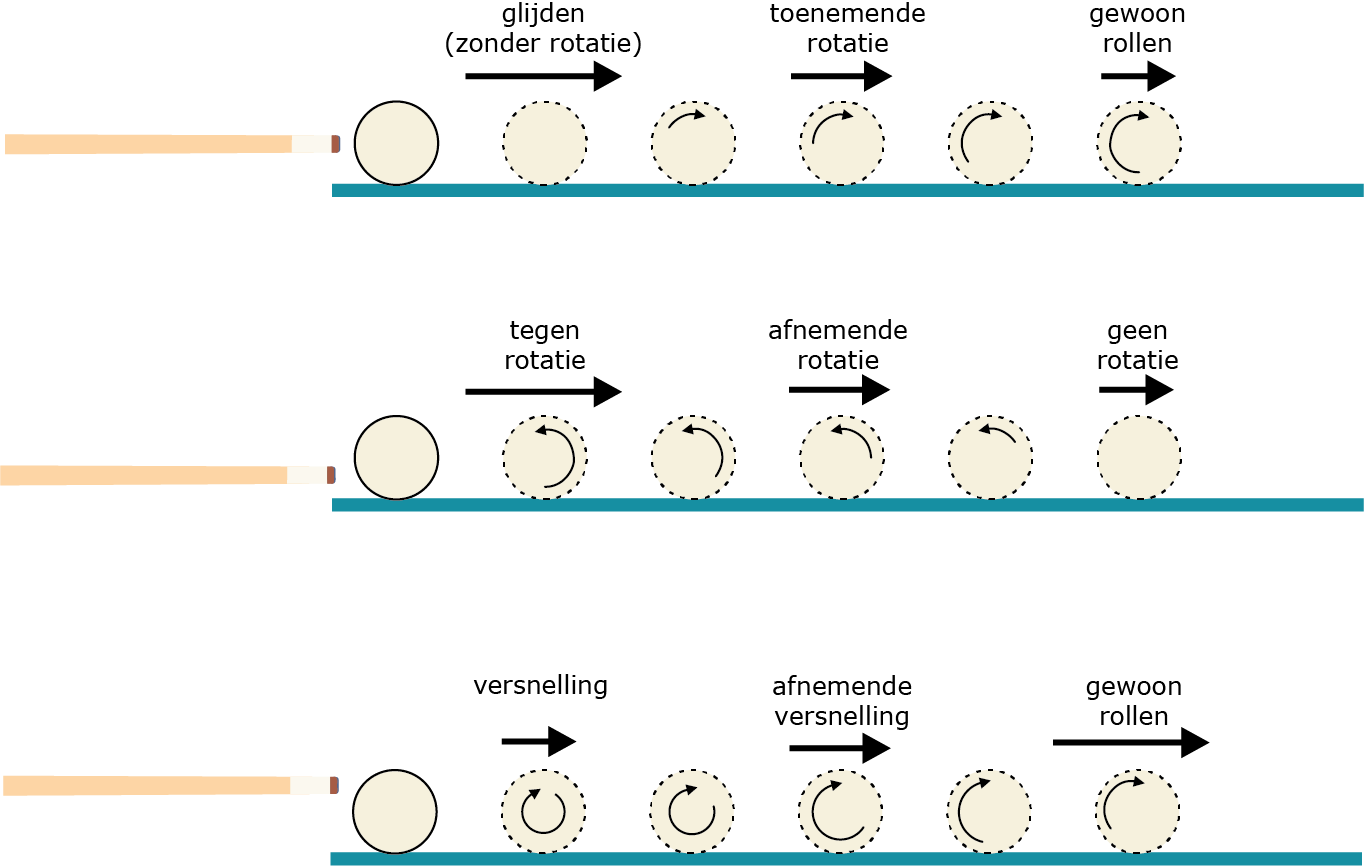
Als je met je keu de cue ball horizontaal raakt, midden tussen de linker- en rechterkant, dan gaat de bal naar voren, in een combinatie van draaien, vooruit bewegen en glijden.

Als je de bal precies in het midden raakt, dus op een hoogte boven de tafel van de straal van de bal, dan zal deze naar voren bewegen en eerst glijden zonder rotatie. Even later zal de bal gewoon rollen, zonder nog te glijden.

Als je de bal heel laag raakt, zal de bal naar voren bewegen, maar het raakpunt zal over de tafel naar voren glijden. Dat geeft na de stoot een vertraging aan de bal, die soms overgaat in een beweging naar achteren.

Als je de bal heel hoog raakt, zal de bal naar voren bewegen, maar het raakpunt op de tafel zal naar achteren glijden. Dat geeft na de stoot een versnelling aan de bal.

In figuur 1 zijn de drie gevallen gevisualiseerd.

Figuur 1

We vragen ons nu af waar we boven het midden van de bal moeten stoten, opdat de bal onmiddellijk en zonder glijden gaat rollen. Deze hoogte boven het midden noemen we $h.$ Dit punt noemen we de sweet spot. Zie figuur 2.

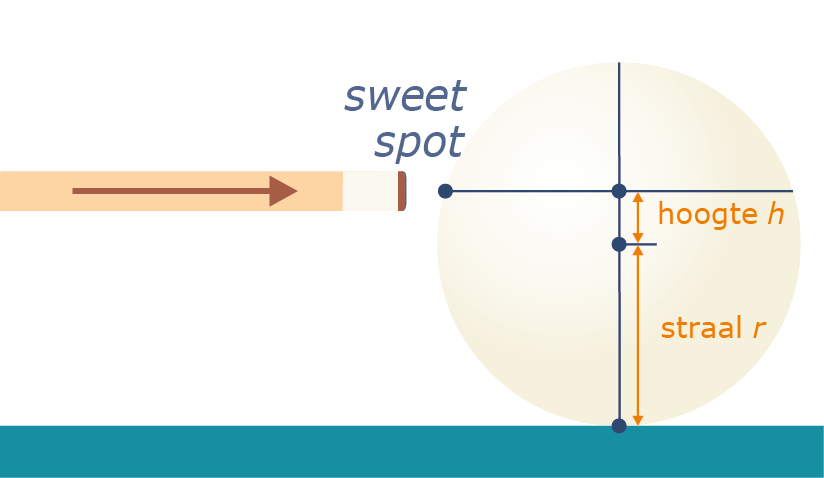
Figuur 2: Voor de stoot

Wat  gebeurt er nu tijdens de stoot? Die duurt heel kort, ongeveer $\Delta t = 0{,}01$ seconde.

Figuur 3: Tijdens de stoot

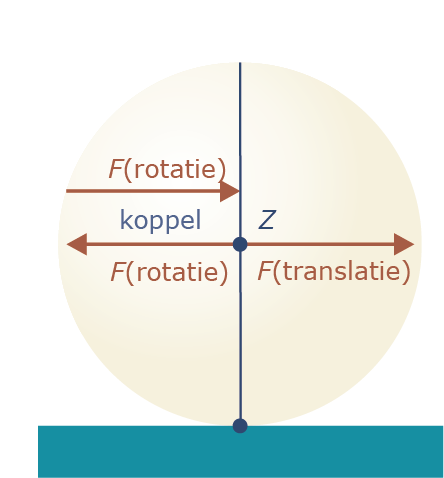
We zoeken naar een beweging naar rechts met een rotatie. De draaisnelheid is $\omega$ (in radialen per seconde). De translatie met snelheid v wordt veroorzaakt door een kracht $F$ die aangrijpt in het zwaartepunt $Z$ van de bal. De rotatie wordt veroorzaakt door een koppel $M$ (zie kader 4) van twee gelijke krachten. We hebben in eerste instantie alleen de kracht $F,$ geleverd door de stoot van de keu, die boven het midden op de bal aangrijpt. Voeg nu twee hulpkrachten $F$ (gelijk aan de kracht van de keu) toe die elkaar opheffen en beide aangrijpen in het zwaartepunt $Z.$ Met z’n drieën zijn ze natuurlijk identiek met alleen de kracht van de keu. Maar we hebben wel iets  bereikt. We hebben een kracht F die aangrijpt in het zwaartepunt en die de bal naar rechts stuurt. Verder hebben we een koppel van twee gelijke en tegengesteld gerichte krachten die voor de rotatie zorgen. Deze koppelkrachten moeten gelijk zijn, omdat de bal anders ook nog een versnelling naar links of rechts krijgt.

We kunnen dan voor de translatie en de rotatie de volgende twee vergelijkingen opschrijven (zie voor het  traagheidsmoment $I$ kader 3):

$$F=ma=m\frac{\Delta v}{\Delta t};$$

$$M=Fh=I\alpha =I\frac{\Delta \omega}{\Delta t}.$$

Hierin is $a$ de versnelling en $\alpha$ de draaiversnelling tijdens $\Delta t.$ We eisen dat de bal gaat rollen en dat het punt van de bal op de tafel niet glijdt. Dan moet gelden:

$$v = \omega r$$

of:

$$\Delta v=r\Delta \omega.$$

Zie figuur 4 voor de tijd na de stoot.

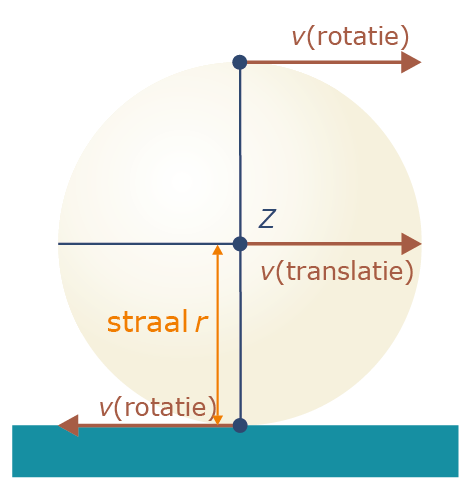
Figuur 4: Na de stoot

Opgave 1

Leid  uit bovenstaande drie vergelijkingen en de formule  voor $I$ van een bol (zie kader 3) af dat geldt:

$$h = \frac{2}{5}r.$$

De sweet spot is de plek waarbij de snelheid het best in te schatten is en het is aan te raden, zeker voor een beginnende poolspeler, om deze hoogte te gebruiken bij het oefenen met het spelen op snelheid. Deze hoogte is onafhankelijk van de kracht tijdens de stoot.

Glijdende bal gaat over in rollen

Als een bal op $t = 0$ met translatiesnelheid $v(0)$ glijdend beweegt langs de $x\mbox{-as}$ met hoeksnelheid $\omega(0) = 0,$ zal er op het onderste punt van de bal een wrijvingskracht $F_w$ naar achteren werken. Het resultaat is dat de bal langzamer gaat glijden en tegelijkertijd begint te rollen. Op een bepaald tijdstip $t=\tau$ zal de bal niet meer glijden en alleen nog rollen. We vragen ons af wat de eindsnelheid $v(\tau)$ dan is, die verder constant  blijft (bij verwaarlozing van de rolweerstand). Bekijk figuur 5.

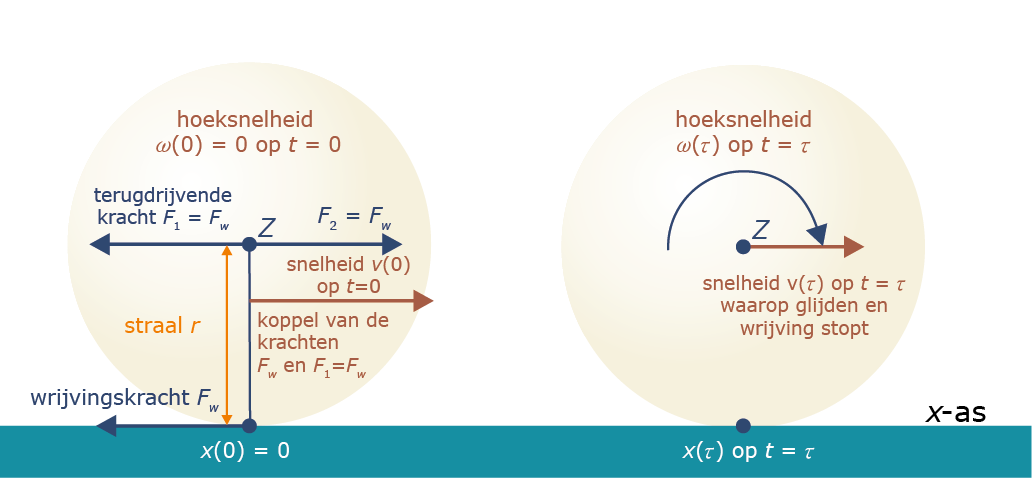
Figuur 5

Om greep te krijgen op de translatie en de rotatie maken we opnieuw gebruik van twee hulpkrachten, beide even groot als $F_w,$ die elkaar opheffen en beide aangrijpen in het zwaartepunt van de bal $Z.$ Dan hebben we een kracht $F_1,$ die aangrijpt in $Z$ en de bal een eenparig vertraagde beweging geeft, en een kracht $F_2,$ die samen met $F_w$ een koppel vormt dat een eenparig versnelde rotatie geeft. We nemen aan dat het glijden stopt op tijdstip $\tau.$

Voor de vertraagde beweging hebben we dan:

$$v(\tau)=v(0)-a\tau.$$

Met voor de vertraging $a:$

$$a=\frac{v(0)-v(\tau)}{\tau}$$

Voor de terugdrijvende kracht $F_1$ geldt:

$$F_1=F_w=\mu mg=ma,$$

zodat geldt:

$$\tau =\frac{v(0)-v(\tau)}{\mu g}.$$

Dan beschouwen we de rotatie. Het moment $M = F_wr$ van de wrijvingskracht veroorzaakt een eenparig versnelde rotatie met hoekversnelling $\alpha.$ Merk op dat de bijdrage aan het moment van $F_2$ ten opzichte van het centrum van rotatie $Z$ gelijk is aan $0,$ omdat $F_2$ in $Z$ aangrijpt.

Voor $\alpha$ geldt dan:

$$\alpha=\frac{M}{I}=\frac{F_wr}{\frac{2}{5}mr^2}=\frac{5}{2}\frac{\mu g}{r}.$$

Voor de hoeksnelheid op $t = \tau$ geldt:

$$\omega(\tau)=\alpha\tau=\frac{5}{2}\frac{\mu g}{r}\tau.$$

Nu stellen we vast dat op het tijdstip $\tau,$ wanneer de bal alleen rolt, het volgende verband geldt tussen de hoeksnelheid $\omega(\tau)$ en de translatiesnelheid $v(\tau):$

$$\omega(\tau)r=v(\tau).$$

Opgave 2

Leid uit de laatste serie formules af dat voor het verband tussen $v(\tau)$ en $v(0)$ geldt:

$$v(\tau)=\frac{5}{7}v(0).$$

Merk op dat dit verband onafhankelijk is van de wrijving tussen bal en tafel. Het zal natuurlijk wel zo zijn dat bij een kleinere wrijvingskracht de weg tot rollen langer is.

Spelen met een glijdende bal (stopshot)

Een stopshot is een term die gebruikt wordt om shots te beschrijven waarbij de cue ball glijdt op het moment van contact met de object ball. Het vergt ervaring, beoordelingsvermogen en vaardigheid om een dergelijk shot op verschillende afstanden te kunnen uitvoeren. Voor een poolspeler is dit shot een belangrijk wapen en hierop wordt veel getraind. Scan de QR-code hiernaast om een demonstratie-video van de auteur te zien.  

De 90-gradenregel

Als de cue ball glijdend en zonder rotatie de object ball niet centraal raakt (zie figuur 6), dan zal de cue ball schuin naar rechts verdergaan en de object ball schuin de andere kant op. De cue ball zal gaan bewegen in de richting van de raaklijn aan beide ballen op het tijdstip van contact. De object ball zal gaan bewegen in de richting hier loodrecht op, dus volgens de verbindingslijn van de twee middelpunten van de ballen op het tijdstip van contact. We gaan deze bewering bewijzen door gebruik te maken van de twee behoudswetten in de mechanica: de wet van behoud van energie en de wet van behoud van impuls.

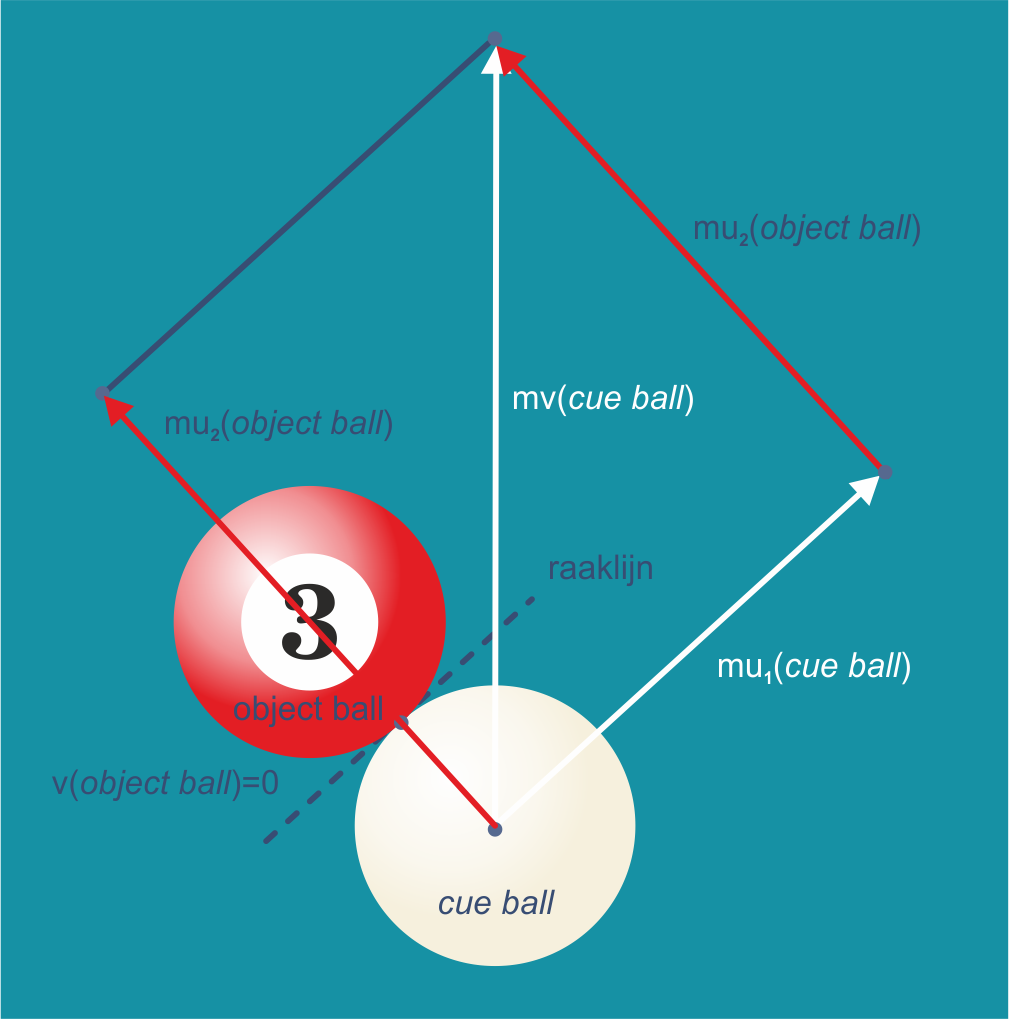
Figuur 6

Eerst de wet van behoud van impuls. De impuls van een voorwerp met massa $m$ en snelheid $v$ is een vector in de richting van de snelheid met grootte $mv.$ De twee impulsen van de cue ball, voor de botsing $mv$ en na de botsing $mu_1,$ staan in de figuur wit getekend. De impuls van de object ball is voor de botsing $0$ en na de botsing $mu_2,$ in de figuur rood getekend.

De wet van behoud van impuls zegt nu dat de vectorsom van de impulsen voor de botsing (alleen vector $mv)$ gelijk is aan de vectorsom van de twee impulsen na de botsing (de vectoren $mu_1$ en $mu_2).$ In de figuur is te zien dat de drie vectoren $mv, mu_1$ en $mu_2$ een driehoek vormen. Omdat ze alle drie evenredig zijn met $m,$ geldt ook dat de drie snelheidsvectoren een driehoek vormen.

Vervolgens geldt ook nog de wet van behoud van kinetische energie. Deze zegt dat de kinetische energie voor de botsing gelijk is aan de kinetische energie na de botsing. Dus:

$$\frac{1}{2}mv^2=\frac{1}{2}mu_1^2 + \frac{1}{2}mu_2^2$$

of:

$$v^2=u_1^2+u_2^2.$$

Dan hebben we dus een driehoek met zijden $v, u_1$ en $u_2$ waarin de stelling van Pythagoras geldt. Daaruit concluderen we dat de snelheden een rechthoekige driehoek vormen en dat dus de twee snelheden na de botsing loodrecht op  elkaar staan: de 90-gradenregel.

Het gaat hier om de snelheden vlak voor en vlak na de botsing. Vanwege het glijden zonder rotatie van de cue ball vlak voor de botsing zullen de twee snelheden vlak na de botsing ook glijdend en zonder rotatie zijn. Daarna gaan de ballen ook roteren. Als de cue ball voor de botsing ook een rotatie had, zouden we in de wet van behoud van kinetische energie natuurlijk ook de rotatie-energie hebben moeten meenemen. Dat zou het probleem ingewikkelder hebben gemaakt. Zie de volgende paragraaf.

De 30-gradenregel

In 2004 introduceerde Dave G. Alciatore de 30-gradenregel. Hij toonde aan dat een rollende cue ball na contact met een object ball een parabolische beweging maakt, waarbij de baan start volgens de 90-gradenregel en eindigt in een richting die ongeveer $30^{\circ}$ maakt met de oorspronkelijk gestoten richting. Dit geldt voor botsingen van $\frac14$ tot $\frac34$ van de baldikte. De regel is onmisbaar voor de huidige generatie poolspelers. Scan de QR-code hiernaast voor een instructie-video van de auteur.

‘Horizontale’ stoot met de keu (pendulum stroke)

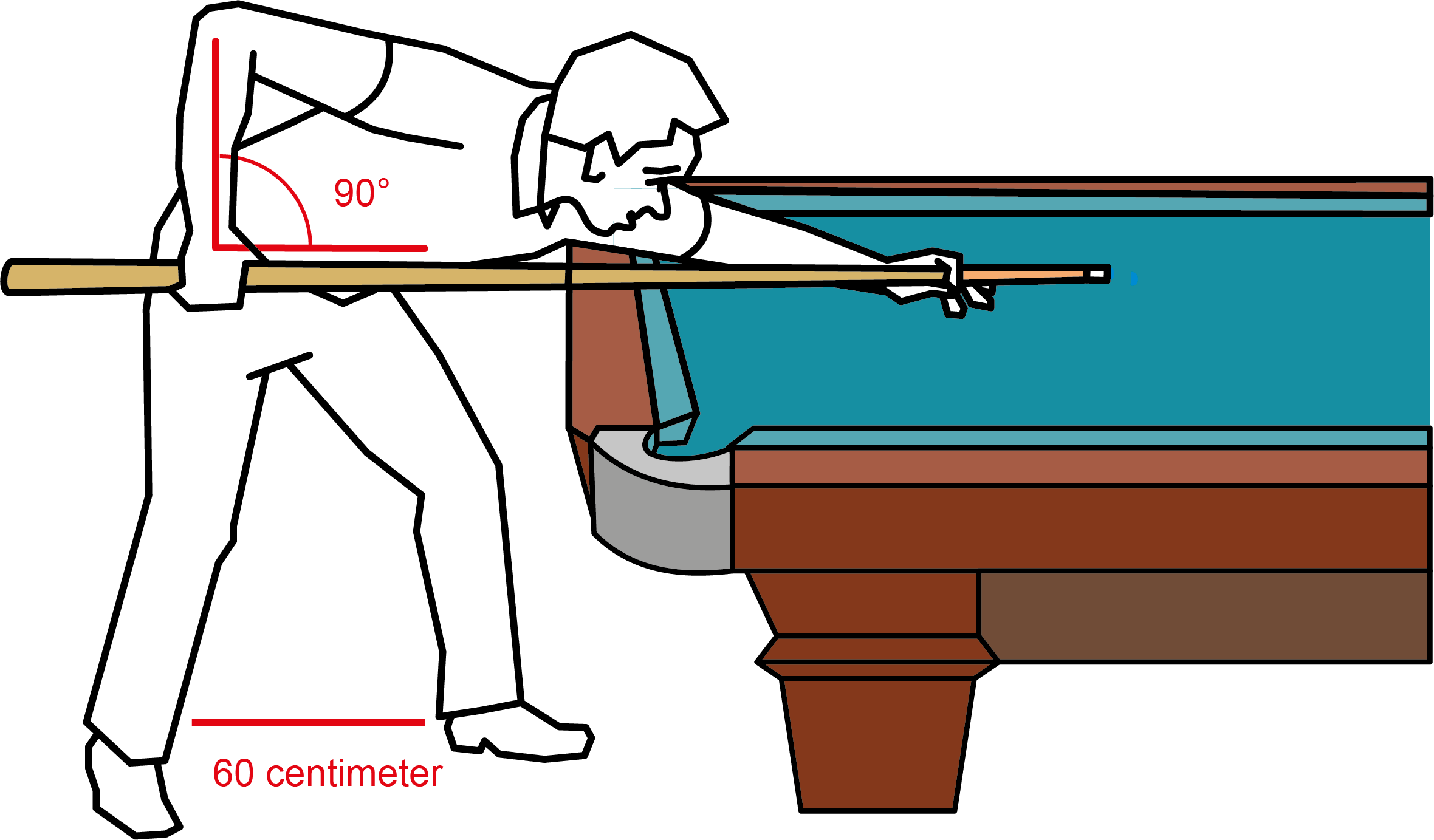
Figuur 7

Het is van belang om bij het stoten van de cue ball de keu vrijwel horizontaal te hebben. We zullen met behulp van de figuur aantonen dat dit vrijwel zo is, als je je onderarm als een soort slinger laat bewegen waarbij het onderste punt van de slinger op gelijke hoogte is als het punt van de keu dat ondersteund wordt door je hand op de tafel. Bekijk figuur 8. Dit is een zijaanzicht, met de elleboog van de biljarter in het midden van de getekende cirkel, de onderarm $\ell$ en de greep om de keu in punt $G_1.$ De andere hand rust in punt $O$ op de tafel.

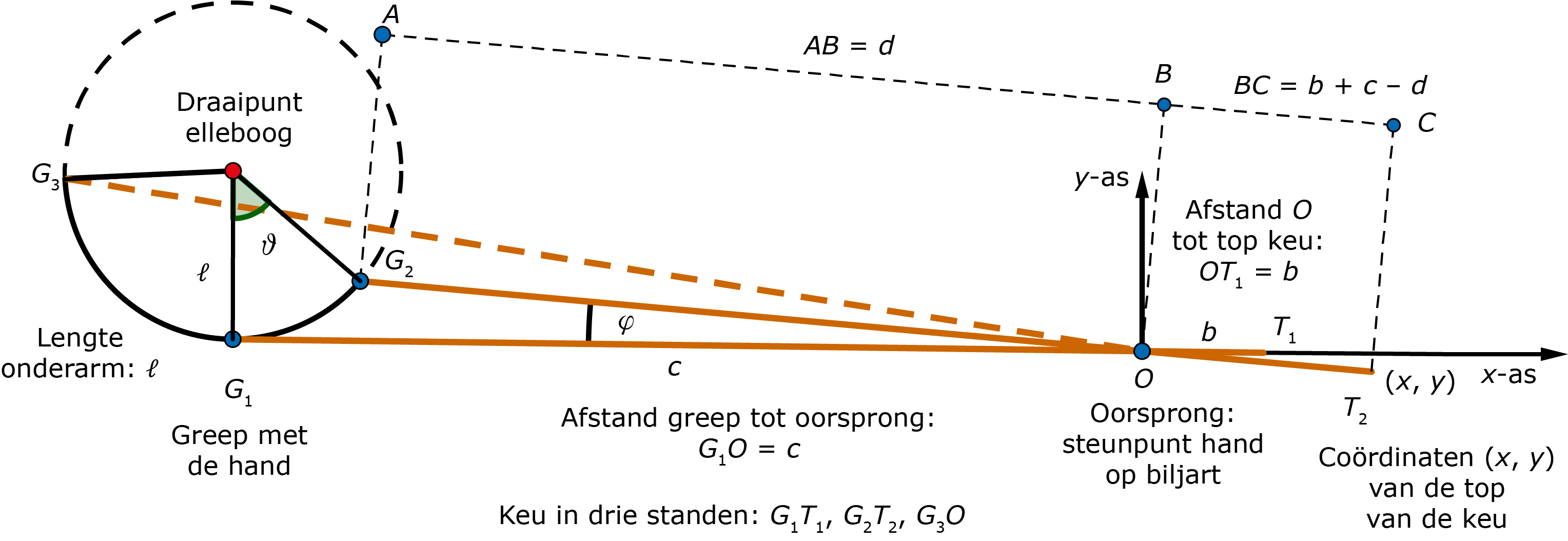
Figuur 8

Links in de figuur zie je dat de greep van de hand $G$ op het einde van de keu een slingerbeweging maakt met de elleboog als middelpunt. Als de keu in $G_1$ is, beweegt de keu horizontaal. De lengte van de keu is dan $c + b,$ waarbij $O,$ het punt tussen $c$ en $b,$ de oorsprong is van het gekozen coördinatenstelsel. Als de hand het verst naar achteren is, in $G_3,$ dan is de top van de keu vrijwel in het punt $O(0,0),$ de hand die de keu ondersteunt. Als de hand van $G_3$ richting $G_1$ beweegt, gaat de top van de keu iets onder de $x\mbox{-as}.$ Maar als de hand in $G_1$ is, is de top van de keu weer op de $x\mbox{-as}.$ Daar raakt de baan van de top van de keu aan de $x\mbox{-as},$ en beweegt dan weer iets naar beneden.

Uit de figuur kun je de volgende formules afleiden:

$$d\cdot \cos(\varphi)=c-\ell\cdot\sin(\vartheta)$$

$$d\cdot\sin(\varphi)=\ell-\ell\cdot\cos(\vartheta).$$

Dit levert $d(\vartheta)$ als functie van $\vartheta:$

$$d(\vartheta)^2=c^2+2\ell^2-2c\ell\cdot\sin(\vartheta)-2\ell^2\cos(\vartheta).$$

Delen van de twee formules op elkaar levert $\varphi(\vartheta)$ als functie van $\vartheta:$

$$\varphi(\vartheta)=\tan^{-1}\left(\frac{\ell(1-\cos(\vartheta))}{c-\ell\cdot\sin(\vartheta)}\right).$$

Daaruit kunnen we de coördinaten van de top van de keu bepalen als functie van $\vartheta:$

$$x(\vartheta)=(c+b-d(\vartheta))\cos(\varphi(\vartheta));$$

$$y(\vartheta)=-(c+b-d(\vartheta))\sin(\varphi(\vartheta)).$$

In onderstaande grafiek zie je de $x-$ en $y-$coördinaat van de top van de keu, beide als functie van de hoek $\vartheta$ die de onderarm maakt tijdens de stoot. Op de horizontale as loopt $\vartheta$ van $-90^{\circ}$ tot $+90^{\circ}.$ Bij $\vartheta = -90^{\circ}$ steekt de onderarm geheel naar achteren, en bij $\vartheta = +90^{\circ}$ steekt de onderarm geheel naar voren. Voor de parameters $b, c$ en $\ell$ hebben we de volgende reële waarden genomen:

$$b = 30\mbox{ cm}, c = 112{,}5\mbox{ cm}, \ell = 35\mbox{ cm}.$$

We gaan de grafieken eens bekijken. Op de horizontale as snijden ze elkaar. Daar is de  top van de keu dus in de oorsprong $(\vartheta \approx -57^{\circ}).$ De stukjes links doen niet mee, want dan zou de top van de keu nog links van de ondersteunende hand zijn $(x < 0\mbox{ en }y > 0).$ Ten eerste zien we dat de $x-$coördinaat over een flink stuk lineair toeneemt, hetgeen overeenkomt met de beweging van de top van de keu naar rechts. We zien verder dat de $y-$coördinaat van de top over een flink stuk vrijwel $0$ is. De top van de keu beweegt dan over een groot deel vrijwel horizontaal (van $\vartheta\approx -57^{\circ}$ tot $\vartheta\approx+110^{\circ}).$ Er is nog een punt met $y = 0$ exact. Dat is als de onderarm verticaal is $(\vartheta = 0^{\circ}).$ De bijbehorende waarde van $x$ is dan $x = 30.$ De lengte van de keu is dus $112{,}5 + 30 = 142{,}5\mbox{ cm}.$

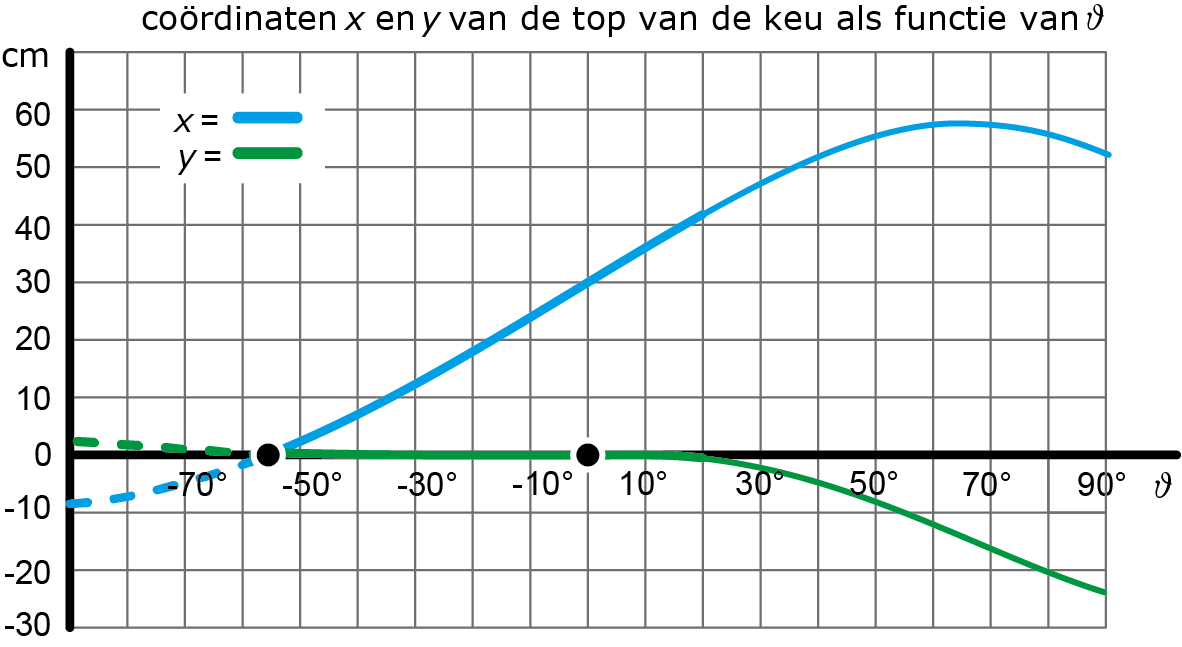
Figuur 9

Door op deze wijze te stoten, is het goed mogelijk om vrijwel horizontaal de cue ball te raken.

Hierna volgen vier kaders met daarin de benodigde natuurkundige achtergrondkennis.

Kader 1: Tweede wet van Newton en eenparig versnelde beweging

Een kracht versnelt of vertraagt de snelheid van een voorwerp en kan iets dat stilstaat in beweging zetten. Als een kracht $F$ op een massa $m$ werkt, zal deze massa eenparig versneld gaan bewegen met een versnelling $a:$ $$a=\frac{F}{m}.$$ De snelheid $v(t)$ op tijdstip $t$ wordt dan:  $$v(t)=v(0)+at.$$ Hierin is $v(0)$ de beginsnelheid in de richting van $F.$ Voor een eenparig vertraagde beweging kunnen we in de formule een minteken zetten. De plaats op de $x\mbox{-as}$ op tijdstip $t$ is dan: $$x(t)=x(0)+t\cdot v_{\rm gemiddeld} = x(0)+t\cdot\frac{v(0)+v(t)}{2}=x(0)+v(0)t + \frac{1}{2}at^2.$$ Hierin is $x(0)$ de plaats op de $x\mbox{-as}$ waar de versnelde beweging begint. Vaak is dat de oorsprong, met dus $x(0) = 0.$

Kader 2: Arbeid, kinetische energie, wrijvingskracht

Als een kracht $F$ op een massa $m$ in de $x\mbox{-richting}$ op een wrijvingsloze tafel werkt over  een afstand $s = x(t) - x(0),$ dan verricht deze kracht een arbeid $W:$ $$W = Fs.$$ Dit betekent dat tijdens het verrichten van deze arbeid de snelheid van m toeneemt en omgezet wordt in kinetische of bewegingsenergie. Er geldt met $x(0) = 0$ en $v(0) = 0:$ $$W=Fs=ma\frac{1}{2}at^2=\frac{1}{2}m(at)^2=\frac{1}{2}mv(t)^2.$$ De grootheid in het rechterlid noemen we de kinetische energie $E_k$ van de bewegende massa: $$E_k=\frac{1}{2}mv^2.$$ Als we wel wrijving hebben tussen een massa $m$ en de vloer waarop deze met snelheid $v$ beweegt, dan werkt er een wrijvingskracht $F_w$ op de massa, die tegen de snelheid in gericht is: $$F_w=\mu mg.$$ De wrijvingskracht is recht evenredig met de kracht van de vloer op $m,$ de normaalkracht. In dit eenvoudige geval is de normaalkracht gelijk aan het gewicht $mg.$ De evenredigheidsconstante noemen we de wrijvingscoëfficiënt $\mu.$ Deze wrijvingskracht is onafhankelijk van de snelheid $v$ van de massa $m.$

Kader 3: Kinetische energie van rotatie of rotatie-energie, traagheidsmoment

Naast de kinetische energie van translatie, die in kader 2 aan de orde is geweest, zit er in een draaiende bol natuurlijk ook kinetische energie van rotatie. We zullen drie verschillende gevallen behandelen. Rotatie-energie $E_r$ van een dunne draaiende ring met straal $r.$ die met hoeksnelheid $\omega$ draait om zijn as. De hoeksnelheid $\omega$ is het aantal radialen per seconde dat een straal van de ring aflegt. Voor de snelheid van een punt op de ring geldt: $$v=\omega r.$$ Stel dat de massadichtheid per meter van de ring gelijk is aan $\lambda.$ Dan is de massa gelijk aan $2\pi\lambda$ en hebben we voor de rotatie-energie: $$E_r=\frac{1}{2}2\pi r\lambda\omega^2r^2=\frac{1}{2}mr^2\omega^2=\frac{1}{2}I_{\rm ring}\omega^2.$$ De grootheid $I$ noemen we het traagheidsmoment van de ring ten opzichte van zijn as. Let op de overeenkomst met de kinetische energie van translatie, waarin de trage massa $m$ vervangen is door het traagheidsmoment $I_{\rm ring}$ en de translatiesnelheid door de hoeksnelheid $\omega.$ Er geldt dus: $$I_{\rm ring} = mr^2.$$ De rotatie-energie van een platte draaiende schijf Voor de rotatie-energie van een dunne schijf geldt een gelijksoortige formule: $$E_r=\frac{1}{2}I_{\rm schijf}\omega^2.$$ Het traagheidsmoment van de schijf $I_{\rm schijf}$ is natuurlijk kleiner dan die van een ring. Na integratie, waarbij je de ring verdeelt in vele smalle ringen, krijg je: $$I_{\rm schijf}=\frac{1}{2}mr^2.$$ De rotatie-energie van een massieve bol met straal $r$ Voor de totale rotatie-energie geldt natuurlijk weer: $$E_r=\frac{1}{2}I_{\rm bol}\omega^2.$$ Het traagheidsmoment van de bol $I_{\rm bol}$ is natuurlijk kleiner dan die van een ring. Na integratie, waarbij je de bol verdeelt in vele dunne schijven, krijg je: $$I_{\rm bol}=\frac{2}{5}mr^2.$$

Kader 4: Koppel van twee krachten veroorzaakt een eenparig versnelde draaiende beweging

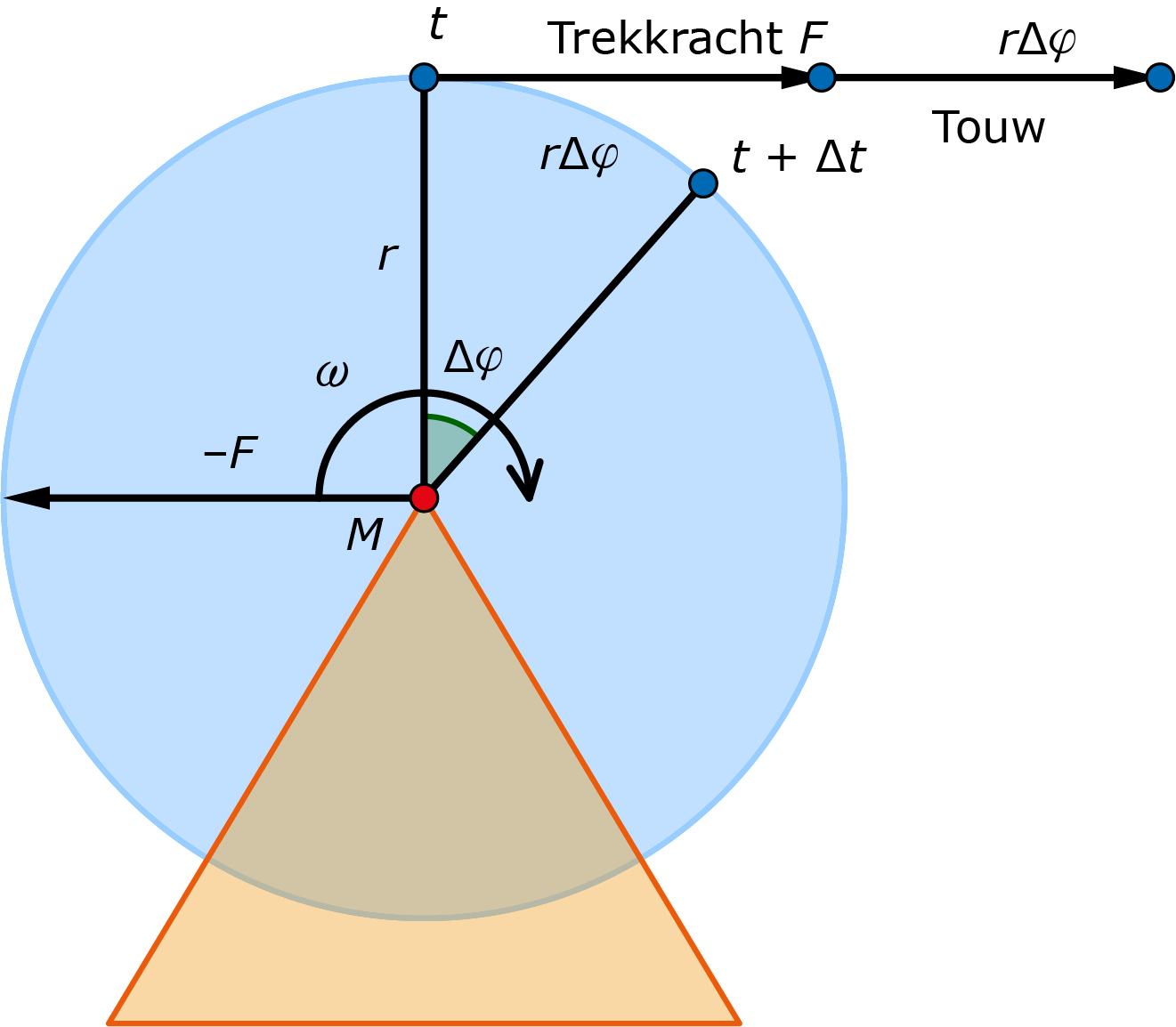
Om een voorwerp alleen maar te laten draaien, hebben we een koppel van twee krachten nodig die even groot zijn en werken langs twee lijnen die niet samenvallen, en tegenovergesteld gericht zijn. Ze moeten even groot zijn, omdat het voorwerp anders in een van de twee richtingen versneld gaat bewegen. En ze moeten langs verschillende lijnen werken, omdat het netto resultaat anders nul is en er geen rotatie komt. Bekijk de figuur. Een schijf wordt in zijn middelpunt ondersteund. Om de schijf zit een touw gewikkeld dat met een constante kracht $F$ het bovenste punt van de schijf naar rechts trekt. De schijf gaat  roteren, maar niet naar rechts bewegen, omdat de driehoekige ondersteuning een reactiekracht $-F$ op het  middelpunt uitoefent. We hebben dan een koppel van twee krachten. De arbeid die verricht wordt als het touw een stukje $r\Delta\varphi$ naar rechts getrokken wordt, is $W=Fr\Delta\varphi.$ De grootheid $\varphi$ is de hoek die een straal heeft afgelegd. De arbeid wordt omgezet in een toename van de rotatie-energie: $$Fr\Delta\varphi=\frac{1}{2}I\Delta\left(\omega^2\right)=I\omega\Delta\omega.$$ Delen door $\Delta t$ geeft, met $\omega=\Delta\varphi/\Delta t$ en de hoekversnelling $\alpha=\Delta\omega/\Delta t{:}$ $$M=Fr=I\alpha.$$ We noemen $M$ het moment van de kracht $F$ ten opzichte van het middelpunt $M.$ Let weer op de overeenkomst tussen de Tweede Wet van Newton $F = ma$ en de overeenkomstige vergelijking voor rotaties $M = I\alpha.$ Voor een eenparig versnelde rotatie gelden overeenkomstige formules als voor een eenparig versnelde beweging: $$\omega(t)=\omega(0)+\alpha t$$ $$\varphi(t)=\varphi(0)+\omega(0)t+\frac{1}{2}\alpha t^2.$$ Hierin is $\varphi$ de hoek van een straal, gemeten vanaf een straal waar $\varphi=0$ gekozen is. Meestal wordt weer op $t=0, \omega(0)=0$ en $\varphi(0)=0$ genomen.

Literatuur en verantwoording

‘Distance required for stun and normal roll to develop’, David G. Alciatore, The Illustrated Principles of Pool and Billiards, http://billiards.colostate.edu, 2003, 2014.

‘Pendulum Stroke Cue Tip Trajectory’, David G. Alciatore, The Illustrated Principles of Pool and Billiards, http://billiards.colostate.edu, 2015.

De natuurkundige afleidingen in dit artikel zijn tot stand gekomen met medewerking van theoretisch fysicus Jan Guichelaar, lid van de redactie van Pythagoras.

 

Wiskunde bij poolbiljarten: Een introductie Het goede punt raken Via de band in de pocket Diverse moeilijkheden bij het potten De baan van de Cue ball