Inzenden kan alleen per e-mail. Stuur je oplossing (getypt of een scan of foto van een handgeschreven oplossing) naar [email protected]. Je ontvangt een automatisch antwoord zodra we je bericht hebben ontvangen.
Voorzie het antwoord van een duidelijke toelichting (dat wil zeggen: een berekening of een bewijs). Vermeld je naam en adres; leerlingen moeten ook hun klas en de naam van hun school vermelden.
Je inzending moet bij ons binnen zijn vóór 1 maart 2019.

OPGAVE 393 [niveau oOO]

Je komt in een hotel terecht met drie dames (Karin, Lieke en Maaike). Je weet dat elk van deze dames of de waarheid spreken of liegen. Een dame die liegt doet dat consequent, dat wil zeggen: élke afzonderlijke bewering is gelogen. Het hotel heeft 10 kamers, genummerd van 1 t/m 10. De dames doen over deze kamers de volgende uitspraken:

• Karin : kamer 1 is vrij, kamer 3 is bezet, kamer 4 is bezet, kamer 5 is vrij, kamer 8 is bezet.
• Lieke: kamer 2 is bezet, kamer 4 is vrij, kamer 10 is vrij.
• Maaike: kamer 6 is vrij, kamer 7 is bezet, kamer 9 is bezet, kamer 10 is vrij.

Hoeveel kamers zijn er minimaal vrij en hoeveel kamers zijn er minimaal bezet?

OPGAVE 394 [niveau oOO]

Dit figuur wordt begrensd door 6 gelijke cirkeldelen. Elk cirkeldeelheeft straal 2. De figuur is 6-voudig draaisymmetrisch en de cirkeldelen raken elkaar.

Wat is de oppervlakte van deze figuur?

 

 

 

 

OPGAVE 395 [niveau ooO]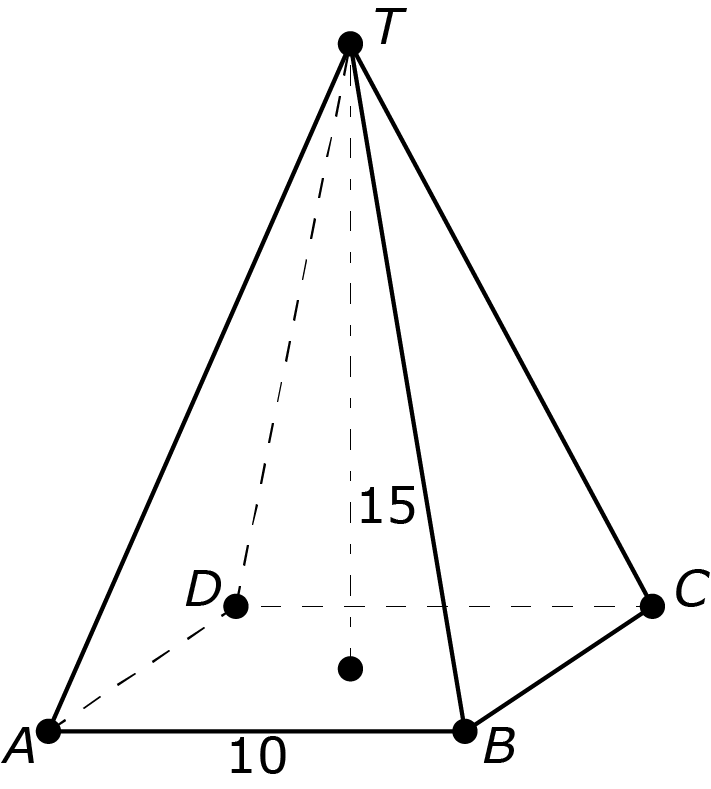

Gegeven een piramide met een vierkant grondoppervlak met zijde 10 en hoogte 15. Bepaal de grootst mogelijke kubus die in deze piramide kan worden geplaatst.

 

 

 

 

 

 

OPGAVE 396 [niveau ooO]

Patrick heeft tien verschillende, strikt positieve getallen. Hij telt ze alle tien bij elkaar op tot het getal A. Ook neemt hij 1 gedeeld door elk van deze getallen en telt deze tien nieuwe getallen op tot het getal B. Ten slotte berekent hij het product A ⋅ B. Kan dit getal kleiner zijn dan 55? Waarom wel of niet?

Bekijk oplossing