Opgave 429 [Niveau oOO]

We bekijken een digitale klok die de tijd in 24-uursnotatie geeft, dus bijvoorbeeld 07:23 en 22:14. Een cijfer wordt weergegeven doordat een aantal van 7 streepjes oplicht. Op welke tijdstippen lichten de minste, en op welke de meeste streepjes op?

Opgave 430 [Niveau oOO]

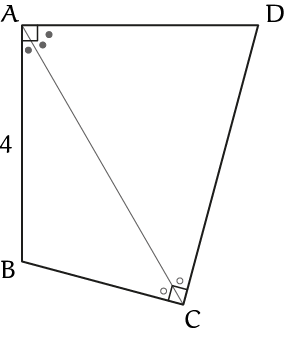
Zij $ABCD$ een vierhoek met $\angle BCD = \angle BAD = 90^{\rm o}$. Er geldt dat $\angle BCA = \angle DCA$ en $2 \cdot \angle BAC = \angle DAC$. Gegeven is dat $|AB| = 4$. Wat is de omtrek van de vierhoek?

Opgave 431 [niveau ooO]

We schrijven het woord $“PYTHAGORAS”$ tien keer achter elkaar op, zonder spaties. Vervolgens strepen we elke letter op een oneven plek weg en houden zo een woord over. We herhalen dit totdat er nog maar één letter overblijft. Welke letter is dit? Welke letter houden we over als we $“PYTHAGORAS”$ honderd keer achter elkaar opschrijven?

Opgave 432 [niveau ooO]

In een regelmatige achthoek bedekken we de buitenrand met $12$ congruente gelijkbenige driehoeken, waardoor er in het midden een vierkant overblijft. Als de oppervlakte van het vierkant $1$ is, wat is dan de oppervlakte van de regelmatige achthoek?
(Met dank aan Harold de Boer.)

Bekijk oplossing