Opgave 445 ^[oOO]

We hangen een schilderij van $180$ bij $220$ cm op aan een muur. We doen dit door er een touwtje omheen te spannen dat 1 cm langer is dan de omtrek van het schilderij. Zie de afbeelding.

Hoe ver hangt de bovenkant van het schilderij dan onder het ophangpunt van het touw?

En als we het schilderij $90$ graden gekanteld ophangen?

Opgave 446 ^[oOO]

Bas schrijft een werkstuk en om dit te doen moet hij natuurlijk een bronvermelding maken. Hij nummert de bronnen in volgorde van wanneer ze voor het eerst gebruikt worden en bronnen mogen ook meerdere keren voorkomen. In zijn bronvermelding verwijst hij naar elke bron met een vast cijfer. Als Bas in totaal $5$ verwijzingen naar een bron heeft in zijn werkstuk, op hoeveel manieren kan zijn bronvermelding er dan uitzien? Voorbeeld: een goede bronvermelding is bijvoorbeeld $1, 2, 1, 3, 2$. Niet goed is $1, 3, 1, 3, 4$ omdat er nu wel een bron $3$ is maar geen bron $2$. Ook niet goed is $1, 3, 1, 2, 2$ omdat bron $3$ nu eerder wordt gebruikt dan bron $2$, maar Bas nummert ze op volgorde.

Opgave 447 ^[ooO]

Beschouw een kring met $360$ mensen. Ze hebben ieder een rode hoed op en een blauwe hoed in hun hand. In het midden van de kring staat de leider. Hij kiest een positief geheel getal $n$, maximaal $360$. De leider wijst dan $n$ mensen aan die naast elkaar staan en zegt dat ze de hoed op hun hoofd moeten verwisselen met die in hun hand. Dan loopt de leider naar de eerst volgende $n$ mensen en zegt hij hetzelfde; zo gaat hij door.

Voor welke keuzes van $n$ zal er ooit een moment zijn waarop iedereen een blauwe hoed op heeft?

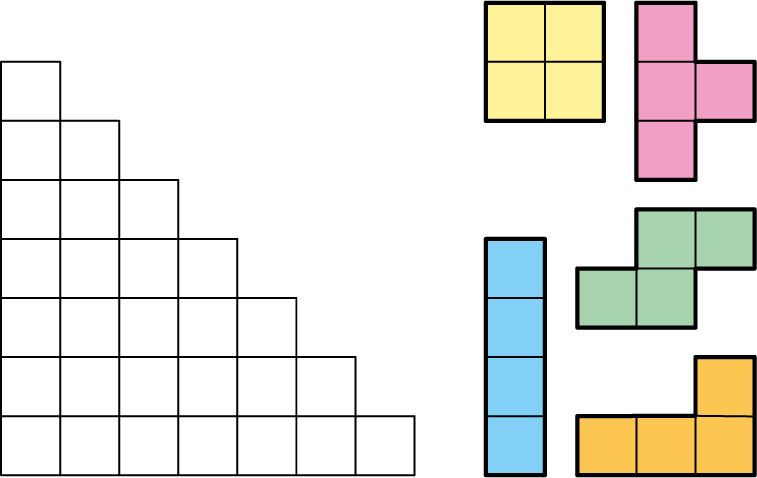
Opgave 448 ^[ooO]

Beschouw een 7-trap, bestaande uit $28$ hokjes. We willen deze opvullen met $7$ tetromino's, waarvan precies $6$ tetromino's dezelfde vorm moeten hebben. Hierbij mogen tetromino's zowel gedraaid als gespiegeld worden. Alle mogelijke tetromino's zijn hieronder weergegeven. 

Bepaal alle manieren om zo'n opvulling te maken.

 

 

Bekijk oplossing