Inzenden kon tot 1 november 2024

Opgave 529 ^[oOO]

Van een verzameling van $100$ verschillende positieve gehele getallen onder de $1000$ tellen we alle cijfers bij elkaar op.

Wat is de kleinst mogelijke uitkomst?

Opgave 530 ^[oOO]

Gegeven is een regelmatige 11-hoek. We kiezen drie verschillende hoekpunten $A$, $B$ en $C$ zodat alle drietallen een gelijke kans hebben om gekozen te worden.

Wat is dan de kans dat het middelpunt van de 11-hoek in driehoek $ABC$ ligt?

Opgave 531 ^[ooO]

Zij $n$ een positief geheel getal en veronderstel dat het getal $7111\dots 111$, dat bestaat uit een zeven gevolgd door n enen, een priemgetal is.

Bewijs dat $n - 1$ deelbaar is door $3$.

Opgave 532 ^[ooO]

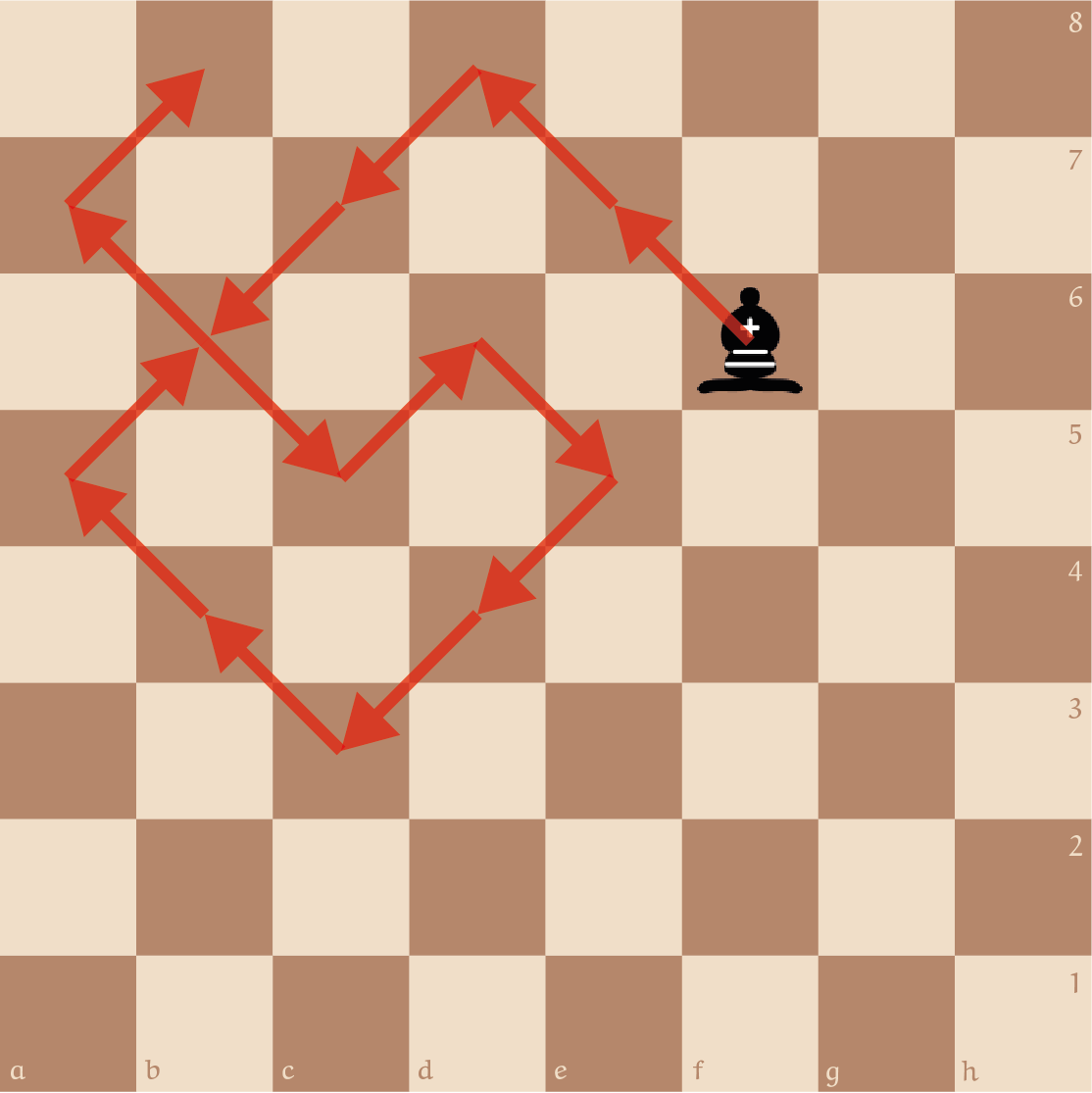
Op een $8\times 8$ schaakbord wil de loper van de zwarte velden graag alle zwarte velden op het bord bezoeken. Hij mag overal beginnen, maar mag per zet slechts één vakje diagonaal bewegen en wil aan het einde weer terugkomen op zijn startveld. In de afbeelding is het begin van een mogelijke route weergegeven.

Hoeveel zetten moet de loper minimaal doen? Bewijs je antwoord!

Je inzending moet bij ons binnen zijn vóór 1 november 2024 via [email protected]