Eén zo'n resultaat haalde in het voorjaar van 2016 dus de krant. Twee wiskundigen, Robert Lemke Oliver en Kannan Soundararajan, kwamen toen met het nieuws naar buiten dat ze bijzondere patronen hadden ontdekt in de priemgetallen.

In het artikel 'Priemraces' (Pythagoras 58-4, februari 2019) hebben we een aardig voorschotje gehad op dit onderwerp. Om even het geheugen op te frissen, er werden daar twee soorten priemraces besproken. De ene race ging tussen priemgetallen van de vorm $4n+1$ en $4n+3$ (het even priemgetal $2$ lieten we daarbij buiten beschouwing), waarbij bleek dat priemgetallen van de vorm $4n+3$ over het algemeen vaker leken voor te komen dan priemgetallen van de vorm
$4n+1$. Beter gezegd, het paard met rugnummer "$4n+3$" loopt in deze race meestal voor op het paard met rugnummer "$4n+1$". Dit fenomeen werd voor het eerst in het midden van de negentiende eeuw ontdekt door de Russische  wiskundige Chebychev, en wordt daarom ook wel Chebychev's bias genoemd. Echter, ondanks het feit dat het paard "$4n+3$" vrijwel altijd op kop loopt, blijkt dat in deze eindeloze paardenrace het paard "$4n+1$" het paard "$4n+3$" oneindig vaak even inhaalt om daarna weer op redelijke achterstand gezet te worden. Iets soortgelijks gebeurt met priemgetallen van de vorm $3n+1$ en $3n+2$. Hier loopt het paard met rugnummer "$3n+2$" vrijwel altijd op kop, maar haalt het paard met rugnummer "$3n+1$" dat paard oneindig vaak in om ook hier daarna weer op redelijke afstand gezet te worden.

Als we de priemgetallen in ons tientallig talstelsel opschrijven, dan eindigen alle priemgetallen, met uitzondering van de priemgetallen $2$ en $5$, allemaal ofwel op het cijfer $1$, ofwel op het cijfer $3$, ofwel op het cijfer $7$, ofwel op het cijfer $9$. In feite hebben we nu een paardenrace met vier paarden, namelijk de vier paarden met respectievelijk de rugnummers "$10n+1$", "$10n+3$", "$10n+7$" en "$10n+9$". Ook in dit geval zal blijken dat elk paard telkens weer eens de koppositie in deze paardenrace zal innemen. Robert Lemke Oliver en Kannan Soundararajan hielden het echter niet bij die vier paarden, maar organiseerden een wedstrijd met zestien paarden. In het tientallig talstelsel hebben we echter maar vier rugnummers "$10n+1$", "$10n+3$", "$10n+7$" en "$10n+9$", dus om nu die zestien paarden uit elkaar te houden plakken we telkens twee van die rugnummers aan elkaar. We krijgen zo de volgende zestien rugnummers:

$10n+1$, $10n+1$		$10n+1$, $10n+3$		$10n+1$, $10n+7$		$10n+1$, $10n+9$
$10n+3$, $10n+1$		$10n+3$, $10n+3$		$10n+3$, $10n+7$		$10n+3$, $10n+9$
$10n+7$, $10n+1$		$10n+7$, $10n+3$		$10n+7$, $10n+7$		$10n+7$, $10n+9$
$10n+9$, $10n+1$		$10n+9$, $10n+3$		$10n+9$, $10n+7$		$10n+9$, $10n+9$

 

Laten we deze zestien rugnummers vanaf nu wat korter opschrijven, als $11, 13, 17, 19, 31, 33, 37, 39, 71, 73, 77, 79, 91, 93, 97$ en $99$. Nu moeten we ons nog een beeld vormen over hoe die paarden in deze race rennen. Nu, in het algemeen kunnen we zeggen dat elk startnummer van de vorm $ab$ is, waarbij de cijfers $a$ en $b$ in de verzameling $\{1, 3, 7, 9\}$ zitten. Als een priemgetal op het cijfer $a$ eindigt, en het eerstvolgende priemgetal eindigt op het cijfer $b$, dan mag het paard met startnummer $ab$ één stap vooruit zetten. Als we nu de paardenrace van start laten gaan dan blijkt al gauw dat de paarden $11$, $33$, $77$ en $99$ helemaal achter in het deelnemersveld blijven hangen, terwijl het paard met rugnummer $91$ de koppositie inneemt en die positie nooit meer afstaat. We hebben hier dus blijkbaar een duidelijke favoriet voor de overwinning, ook al is het een wedstrijd die nooit eindigt. 

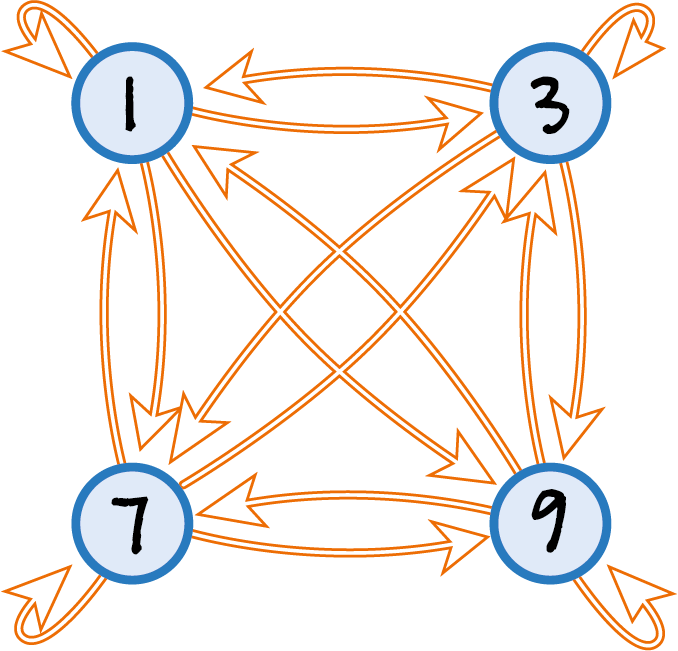
Figuur 1

We kunnen die paarden ook voorstellen door de pijlen in de graaf in figuur 1.

Een graaf is hier een wiskundig begrip dat zijn (fonetische) oorsprong vindt in het Engelse woord "graph". Een graaf bestaat uit een aantal punten (in dit voorbeeld de punten $1$, $3$, $7$ en $9$) en een aantal lijnen tussen die punten. In ons geval zijn die lijnen pijlen, dan spreek je van een gerichte graaf. In deze graaf komen alle mogelijke pijlen voor, en in dat geval spreken we ook wel van een volledige graaf. De grafen die in dit artikel aan de orde komen zijn overigens allemaal volledige grafen. Een pad in de graaf dat start en eindigt in eenzelfde punt en waarvan de lengte minstens $1$ is, noemen we een cykel.

Wat de paarden waar we het over hadden betreft, het rugnummer ($ab$) van elk paard wordt nu gevormd door het cijfer bij de staart van een pijl ($a$) en het cijfer bij de kop van de pijl ($b$). Telkens als we ons door de eindcijfers van de priemgetallen bewegen volgen we de pijlen en mag het paard dat bij de betreffende pijl hoort één stap vooruit. De graaf hierboven blijkt nogal ingewikkeld, omdat je allerlei verschillende lussen kunt doorlopen, zoals van $1$ naar $3$ naar $7$ en dan weer terug naar $1$ (als voorbeeld van een cykel met lengte $3$), of van $1$ naar $9$ naar $7$ naar $3$ en dan weer terug naar $1$ (als voorbeeld van een cykel met lengte $4$). Met zestien paarden kunnen er dus heel wat dingen gebeuren tijdens de race, en wordt het wel ingewikkeld om de wedstrijd en alles wat er tijdens de wedstrijd gebeurt goed te volgen.

Gelukkig hebben we ook eenvoudigere priemraces, namelijk die met "$4n+1$" en "$4n+3$". Hier hebben we maar twee cijfers namelijk $1$ en $3$, en daarmee kunnen we vier combinaties van twee cijfers maken. De graaf wordt dan ook een stuk eenvoudiger, zoals je ziet in figuur 2.

Figuur 2

In dit geval blijkt dat de paarden met
rugnummers $13$ en $31$ al snel de koppositie in onze priemrace innemen en de paarden $11$ en $33$ op geruime afstand daar achteraan lopen. Met behulp van het Python programma uit het artikel 'Priemraces' is de uitkomst van deze race berekend. Het resultaat zie je in grafiek 1. De groene en de oranje kromme vallen precies over elkaar. Kun je nagaan waarom? Deze graaf is wel een stuk eenvoudiger, maar ook weer erg saai. Je kunt alleen maar op hetzelfde punt (de punten $1$ en $3$) blijven, of van punt wisselen. Als vier cijfers zoals we in het decimale talstelsel zagen, al erg ingewikkeld wordt, en twee cijfers te saai is, blijft ons niets anders over dan te zoeken naar iets met drie cijfers, zodat het noch saai, noch al te ingewikkeld wordt.

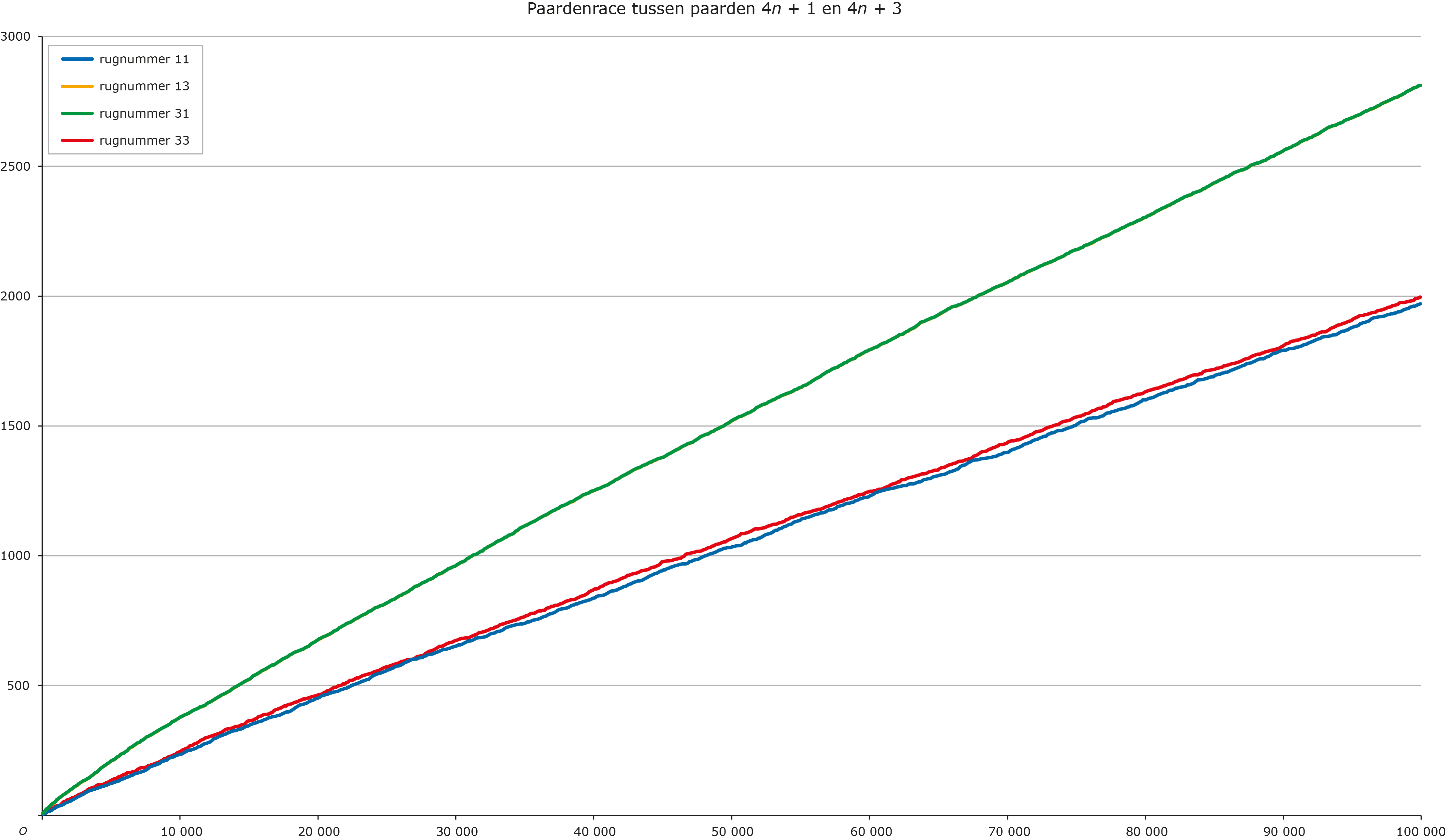
Grafiek 1

Maar hoe kom je aan zoiets met drie cijfers? Zie jij het al? Dat blijkt nog niet zo makkelijk te zijn, maar we hebben ook hier een oplossing voor, zoals we nog zullen zien.

De resultaten van Lemke Oliver en Soundararajan, gingen echter precies om de hier beschreven priemraces, waarbij de gebruikte pijl bepaalt welk paard de volgende stap mag maken. Wedstrijden waarbij er duidelijke favorieten zijn, die de kopposities innemen, met daarnaast paarden die gedoemd zijn in de achterhoede van de race te blijven. Een fenomeen waar de onderzoekers zelf door verrast waren, temeer omdat dit, voor doorgewinterde wiskundigen toch eenvoudige fenomeen, nog nooit eerder waargenomen was. Eenmaal zo'n fenomeen ontdekt, ga je je afvragen welke andere voor de hand liggende fenomenen hebben we tot nu toe nog niet onderkend? In het eerder genoemde krantenartikel werd de reactie van de Nederlandse wiskundige Frits Beukers (universiteit Utrecht) geciteerd: "Mijn belangrijkste vraag is eigenlijk of er met je boerenverstand ook te begrijpen is waarom priemgetallen elkaar afstoten". Met afstoten wordt hier bedoeld dat als een priemgetal eindigt op een cijfer a, de kans aanzienlijk kleiner dan gemiddeld is dat we bij het eerstvolgende priemgetal weer dezelfde a als eindcijfer hebben (dus kleiner dan 25%). Met andere woorden, de paarden met rugnummers van de vorm aa lopen altijd achteraan in deze priemraces, en die met rugnummers $ab$ ($a$ verschillend van $b$) lopen daar al snel met ruime afstand op voor, waarbij er vaak ook nog een unieke koploper of anderszins minstens een kopgroep is.

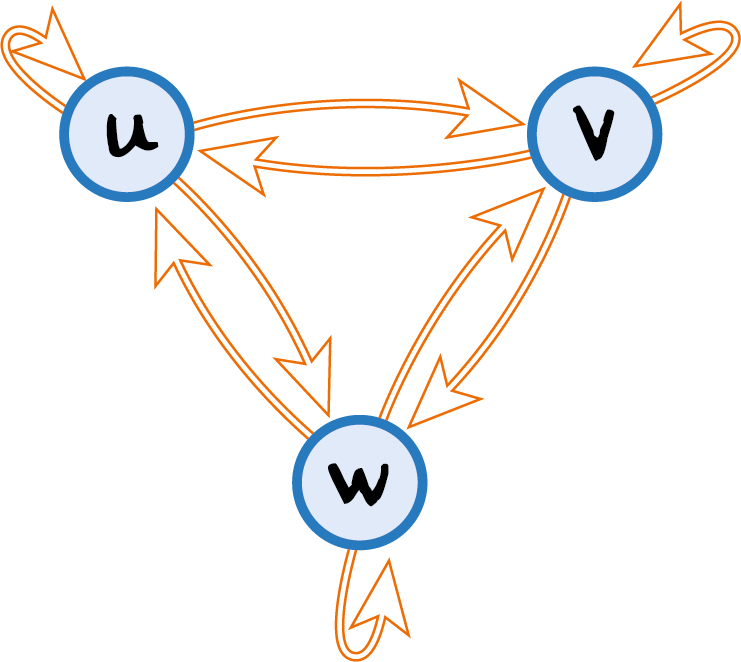
Figuur 3

In het tientallige stelsel blijkt er één koploper te zijn, namelijk het paard met rugnummer $91$; in het viertallige stelsel ontstaat er een kopgroepje van twee: de paarden met rugnummers $13$ en $31$. Nu, met louter boerenverstand gaat het ons niet lukken om dit fenomeen helemaal te doorzien, maar we kunnen wel een stukje in die richting komen. Als we daarbij iets kunnen bedenken waarbij we maar drie verschillende eindcijfers hebben, dan kunnen we wat meer zien dan bij de saaie
gevallen met maar twee verschillende eindcijfers, terwijl het nog niet zo ingewikkeld wordt als in het decimale geval waar er vier verschillende eindcijfers zijn. Een "slimme" keuze van een $q$-tallig talstelsel, zodat we voor de priemgetallen
maar drie eindcijfers hebben, bestaat niet. In de voorbeelden $q = 3$ en $q = 4$, zagen we dat we slechts twee verschillende cijfers hadden. Voor bijvoorbeeld $q = 10$ zagen we dat we al aan vier verschillende eindcijfers zitten. Ook
voor $q = 5$ of $q = 8$ hebben we vier verschillende eindcijfers en dus zestien paarden, terwijl voor bijvoorbeeld $q = 6$ we weer slechts twee cijfers hebben en dus maar vier paarden. Maar wat mogen we eigenlijk verwachten van "iets" met drie verschillende eindcijfers, nog los van de vraag of zo "iets" bestaat? Nou, stel dat we maar drie verschillende eindcijfers hebben, en stel de eindcijfers voor door $u$, $v$ en $w$, dan krijgen we de graaf in figuur 3.

In deze graaf zijn de mogelijkheden beperkt. We hebben de paarden met rugnummers $uu$, $vv$ en $ww$, waarvan Oliver Lemke en Soundararajan hadden ontdekt dat deze paarden altijd achteraan lopen. Verder hebben we zes paarden met "afstotende" rugnummers zoals Frits Beukers die in het citaat noemde, de rugnummers $uv$, $uw$, $vu$, $vw$, $wu$ en $wv$. Deze zes paarden kunnen we nu in twee groepen verdelen, namelijk de paarden $uv$, $vw$ en $wu$, die samen de rechtsdraaiende cykel $uvw$ in de graaf vormen, en de paarden $uw$, $wv$ en $vu$, die samen de linksdraaiende cykel $uwv$ in de graaf vormen.

Er zijn nu voor deze zes paarden drie verschillende mogelijkheden: 

Mogelijkheid 1

De zes paarden vormen tezamen één grote kopgroep, hetgeen wil zeggen dat er geen voorkeur is in de richting (rechtsom of linksom) waarmee we door de graaf lopen; we blijven gewoon wat heen en weer gaan zonder voorkeur.

Mogelijkheid 2

De paarden $uv$, $vw$ en $wu$ vormen met zijn drieën een kopgroep en de paarden $uw$, $wv$ en $vu$ lopen in het middenveld, hetgeen er op neer komt dat we een voorkeur hebben om rechtsdraaiend door de graaf te lopen.

Mogelijkheid 3

De paarden $uw$, $wv$ en $vu$ vormen met zijn drieën een kopgroep en de paarden $uv$, $vw$ en $wu$ lopen in het middenveld, hetgeen er op neer komt dat we een voorkeur hebben om linksdraaiend door de graaf te lopen. 

Enfin, we weten dus nu al wat we kunnen verwachten, terwijl we de paarden zelf nog niet eens hebben. Deze verwachting is er omdat deze graaf net niet te saai is en ook weer niet te ingewikkeld. 

Maar nu nog de paarden zelf. We gaan daarvoor kijken naar de eindcijfers van de priemgetallen in het decimale talstelsel. Maar dan hebben we toch vier verschillende eindcijfers? Ja, maar we gaan één van die vier buiten spel houden. Zomaar wat priemgetallen zelf willekeurig kiezen om zo een eindcijfer buiten spel te houden, is geen optie. Dan kunnen we elk van de drie mogelijkheden afdwingen door telkens de juiste keuzes te maken. We moeten dus wel iets doen wat eerlijk lijkt en waar we ons aan een streng selectieprincipe van de te kiezen priemgetallen moeten houden. 

De Franse wiskundige Sophie Germain (1776-1831), waarnaar in Parijs ook een straat is genoemd, blijkt ons met haar Sophie Germain-priemgetallen aan de juiste paarden te kunnen helpen. Een priemgetal $p$ heet een Sophie Germain-priemgetal, als niet alleen $p$ priemgetal is, maar ook $2p+1$ een priemgetal is. De eerste Sophie Germain-priemgetallen zijn $2, 3, 5, 11, 23, 29, 41, \dots$ en zijn in de On-line Encyclopedia of Integer Sequences (OEIS) terug te vinden als reeks A005384 (OEIS.org/A005384). Als we de twee Sophie Germain-priemgetallen $2$ en $5$ uitsluiten, dan houden we louter priemgetallen over die in het decimale talstelsel eindigen op een $1$, een $3$ of een $9$; precies wat we graag zouden willen. 

Als we nu een paardenrace houden met de paarden uit de stal van Sophie Germain, de paarden met rugnummers $11$, $13$, $19$, $31$, $33$, $39$, $91$, $93$ en $99$, dan blijkt dat er tijdens de race drie groepjes van elk drie paarden
ontstaan: de kopgroep met paarden $13$, $39$ en $91$, de middengroep met paarden $19$, $93$ en $31$ en een slotgroep met de paarden $11$, $33$ en $99$. Omdat de paarden $13$, $39$ en $91$ in de kopgroep zitten, noemen we deze
rechtsdraaiende priemgetallen zoals in de titel van dit artikel aangegeven. In grafiek 2 is de race in beeld gebracht. 

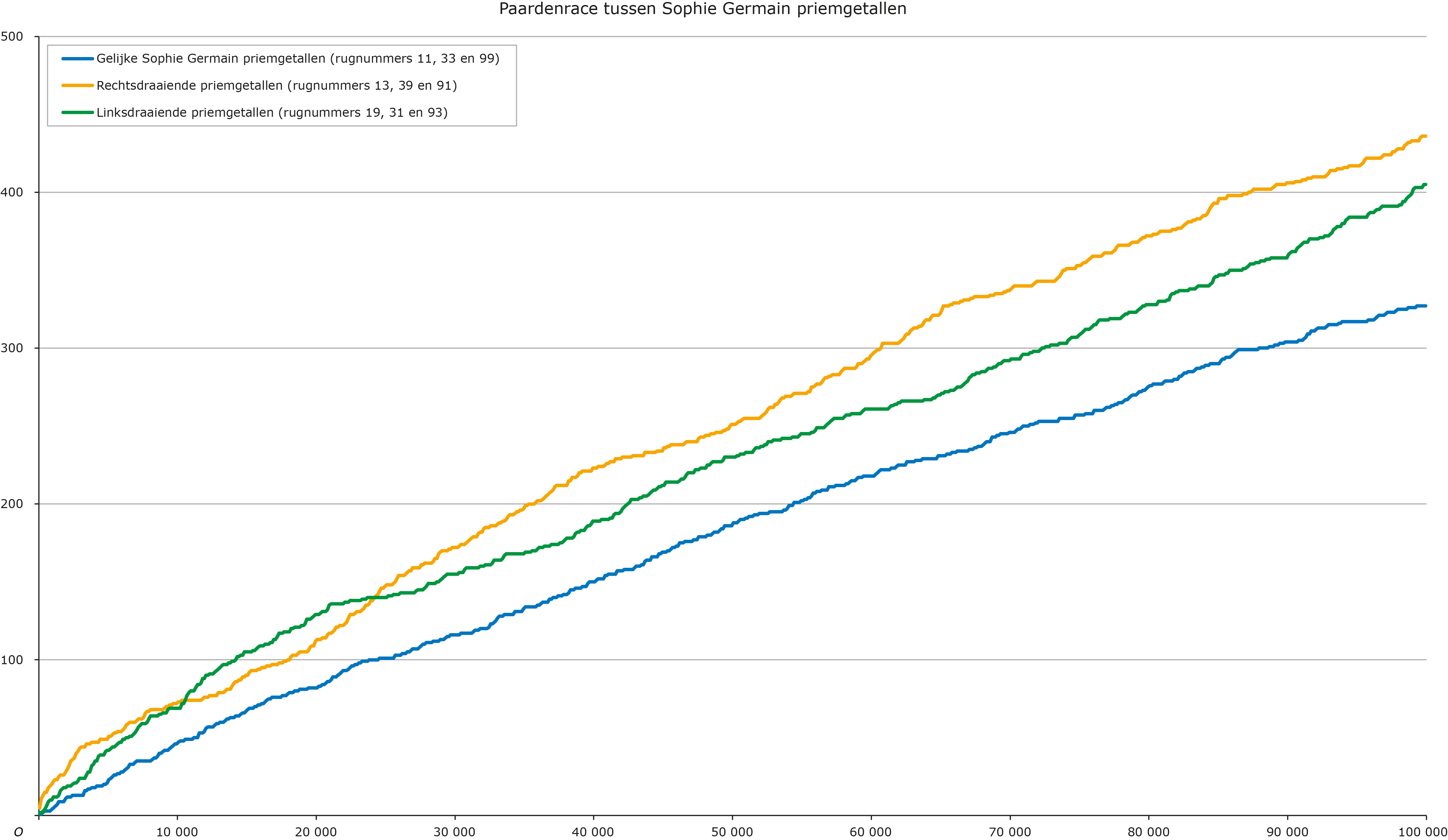
Grafiek 2

We hoeven het niet te laten bij deze Sophie Germain priemgetallen. We kunnen een andere selectie hanteren door gebruik te maken van priemtweelingen. We noemen een paar van twee priemgetallen een priemtweeling als ze onderling slechts een verschil van $2$ hebben. Elk paar $(p, p+2)$ is dus een priemtweeling als zowel $p$ als $p+2$ priem zijn. Voor de kleinere van een priemtweeling, $p$, hebben we de reeks A001359 in de OEIS, die begint met de getallen $3, 5, 11, 17, 29, 41, 59$. Sluiten we nu de getallen $3$ en $5$ uit, dan houden we uitsluitend priemgetallen (de kleinere van de priemtweelingen dus) over die eindigen op de cijfers $1$, $7$ of $9$. Ook in dit geval zien we dat de paardenrace drie groepen oplevert: de kopgroep met rugnummers $17$, $79$ en $91$ (de rechtsdraaiende cykel weer), een middengroep met de rugnummers $19$, $97$ en $71$ (de linksdraaiende cykel) en de staartgroep met startnummer $11$, $77$ en $99$.

De uitkomst van de race is met het Python programma in grafiek 3 zichtbaar gemaakt.

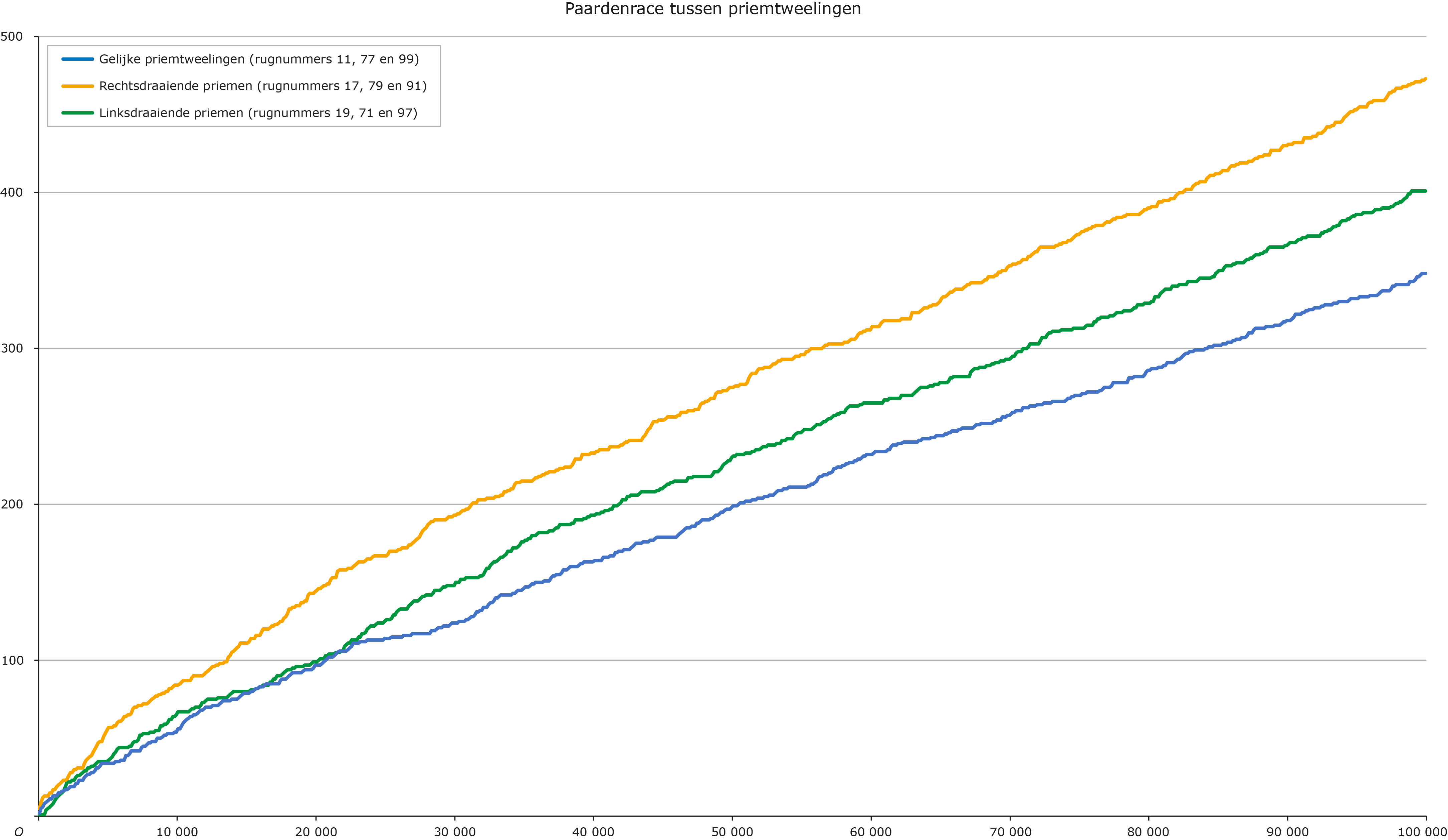
Grafiek 3

Naast Sophie Germain-priemgetallen of priemtweelingen zouden we nog heel veel andere selectiemechanismen kunnen kiezen. In het algemeen zou je kunnen kijken naar paren van priemgetallen $(p, xp + y)$, dus die priemgetallen $p$, waarvoor ook $xp + y$ priem is, met $x$ en $y$ positieve gehele getallen. Voor de Sophie Germain-priemgetallen hebben we $x = 2$ en $y = 1$ voor de kleinere van de priemtweelingen hebben we $x = 1$ en $y = 2$. Als $xp + y$ ook priemgetal moet zijn, dan mogen de getallen $x$ en $y$ alleen $1$ als gemeenschappelijke deler hebben. Zouden namelijk $x$ en $y$ een getal $d$ als gemeenschappelijke deler hebben $(d > 1)$, dan zou elk getal $xp + y$ deelbaar zijn door $d$. Met behulp van paren van priemgetallen hebben we een onuitputtelijk aantal mogelijkheden om priemgetallen te selecteren. Onbekend is of elk van zulke selecties een kopgroep in de priemraces oplevert met de rechtsdraaiende rugnummers. Ons boerenverstand heeft ons namelijk wel ingefluisterd dat er verschillende groepen kunnen ontstaan tijdens de priemraces, maar we hebben nog steeds geen aanleiding te veronderstellen welke, rechtsdraaiende of linksdraaiende, startnummers in de kopgroep lopen, en tot een aanleiding hiervoor zal het in dit artikel ook niet komen ook.

Zover hebben we op een objectieve manier de eindcijfers van de priemgetallen gereduceerd tot slechts drie mogelijke eindcijfers, maar we kunnen ook veel botter te werk gaan. Met de botte bijl nemen we namelijk gewoon alleen die priemgetallen die eindigen op cijfers in de verzameling $\{1, 3, 7\}$ of $\{1, 3, 9\}$ of $\{1, 7, 9\}$ of $\{3, 7, 9\}$. In elk van die gevallen blijkt echter ook dat de rechtsdraaiende startnummers de kopgroep vormen. Kiezen we voor de verzameling $\{1, 3, 9\}$ of $\{1, 7, 9\}$ dan blijkt dat de afstand tussen de kopgroep van rechtsdraaiende en de middengroep van linksdraaiende startnummers groter is, dan wanneer we kiezen voor de verzameling $\{1, 3, 7\}$ of $\{3, 7, 9\}$. Dat de verzamelingen $\{1, 3, 9\}$ en $\{1, 7, 9\}$ veel duidelijkere kopgroepen opleveren verklaart ook enigszins waarom in het oorspronkelijke probleem van Lemke Oliver en Soundararajan het paard $91$ op kop loopt; $91$ komt namelijk in zowel $\{1, 3, 9\}$ als $\{1, 7, 9\}$ voor in de rechtsdraaiende cykel, de kopgroeppaarden met de grootste voorsprong op de middengroep.

Is het je een beetje gaan tollen met al die verschillende paardenraces? Dat is niet zo vreemd. Ga eens zelf zo'n paardenrace programmeren en je kunt het wedstrijdverloop als toeschouwer aanschouwen. Dan zie je het voor eigen ogen. Natuurlijk kun je ook je eigen selectiemechanisme kiezen voor een andere paardenrace. Daarvoor zou je de genoemde priemparen $(p, xp + y)$ kunnen gebruiken. Ook zou je een ander talstelsel kunnen nemen, bijvoorbeeld het twaalftallig stelsel met de
cijfers $0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A$ en $B$. In het twaalftallig stelsel eindigen alle priemgetallen (behalve $2$ en $3$) allemaal op de eindcijfers $1, 5, 7$ of $B$. Ook hier kun je weer selectiemechanismen bedenken om drie uit die vier eindcijfers te selecteren. 

Het onderwerp is nog vrij nieuw in de wiskunde zoals we in het begin al zeiden. De voorbeelden die we hier hebben gegeven van selecties van eindcijfers hebben we zelf bedacht om zodoende wat inzicht te geven in de resultaten van Oliver Lemke en Soundararajan, en andere experimenten (paardenraces) zouden wel eens nog nooit door iemand zijn kunnen gedaan, zodat daar best nog eens een verrassing tussen zou kunnen zitten. Heb jij experimenten gedaan met andere selectiemechanismen of in een ander talstelsel dan de talstelsels met grondtal $3, 4$ of $10$, laat ons dan jouw resultaten weten. Het zou natuurlijk verrassend zijn als we ook linksdraaiende startnummers in een kopgroep tegenkomen, en dat geval valt vooralsnog niet uit te sluiten, maar ook een bevestiging van andere rechtsdraaiende kopgroepen zijn zeker welkom om te weten. Wat dat betreft, veel succes met jouw experimenten. Wij zijn benieuwd naar de reacties, en wie weet, hou je er zelf ook nog een leuk profielwerkstuk aan over. 

De uitslag van de Lemke Oliver en Soundararajan paardenrace (voor decimale cijfers) is overigens, dat het paard met startnummer $91$ uiteindelijk in winnende positie blijft, gevolgd door de paarden $13$ en $79$, daarna de paarden $17$ en $39$, dan het paard $37$ (tot hier allemaal paarden met rechtsdraaiende rugnummers), dan het paard met rugnummer $73$, vervolgens de paarden $71$ en $93$, dan de paarden $31$ en $97$, met daarachter weer het paard met rugnummer $19$ (allemaal paarden met linksdraaiende rugnummers, waarmee we alle afstotende rugnummers hebben gehad), dan de paarden met rugnummers $11$ en $99$, en tot slot de paarden met startnummers $33$ en $77$. Eer de definitieve posities van de paarden in deze race bepaald zijn, moet je als toeschouwer wel wat geduld op kunnen brengen, want pas na priemgetallen van de orde $510\,000\,000\,000$ worden de definitieve posities ingenomen.

De uitslag van de Lemke Oliver en Soundararajan paardenrace in het twaalftallig stelsel loopt als volgt: er is een kopgroepje van de paarden met rugnummers $B1$ en $57$, gevolgd door de paarden met rugnummers $15$ en $7B$, dan de paarden met rugnummers $17$, $7B$, $B7$ en $71$, dan de paarden $1B$ en $75$, gevolgd door de paarden $B7$ en $51$, de paarden $11$ en $BB$ en tot slot de paarden $55$ en $77$.

Tot slot, in verband met de paardenraces van Lemke Oliver en Soundararajan, wordt ook vaker de term samenzwering gebruikt. Het duidt hier op een wiskundige samenzwering tussen de priemgetallen onderling, die als het ware onder elkaar hebben afgesproken om de voorkeur te geven aan afstotende eindcijfers (de rugnummers met afstotende cijfers). Het begrip samenzwering kennen we ook in de natuurkunde, namelijk de zogenaamde verstrengelde deeltjes (elektronen of lichtdeeltjes) in de kwantummechanica. Hier gaat het om twee deeltjes die zo ver van elkaar verwijderd zijn, dat ze binnen de gestelde tijd onmogelijk onderling kunnen communiceren over hun gedrag, maar waarbij het gedrag van het ene deeltje bij een waarneming het gedrag van het andere, verstrengelde deeltje, volledig bepaalt. Dit is in de natuurkunde een nog altijd onopgeloste paradox tussen de kwantummechanica en de relativiteitstheorie, die ook wel bekend staat als de Einstein-Podolsky-Roosen paradox, en nog altijd veel filosofisch ingestelde natuurkundigen bezig houdt. Leuk daarom dat de term samenzwering niet alleen meer in de natuurkunde een begrip is geworden, maar ook in de wiskunde een begrip lijkt te worden. Het volledige mechanisme waarmee de priemgetallen hun samenzwering realiseren, valt namelijk niet zomaar met het boerenverstand te begrijpen. We hebben er hier hooguit wat meer begrip voor gekregen en met name wat meer gevoel bij gekregen. Maar een beetje mystiek heeft zo ook zijn charme.