Aan het eind van de negentiende eeuw veronderstelde men dat lichtstralen of golven een medium nodig hadden om zich in voort te planten, net zoals watergolven water nodig hebben en geluidsgolven lucht. Men noemde dit de ether. Maar men
kon met experimenten niet aantonen dat de aarde door de ether bewoog. Stralen die met de aarde mee zouden bewegen, en stralen daar loodrecht op, zouden in experimenten, o.a. door Albert Michelson (1852-1931) en Edward Morley (1838-1923), een verschillend meetresultaat moeten geven. Maar dat bleek niet zo te zijn. Het was alsof er geen ether bestond.

Albert Einstein (1879-1955) heeft toen in 1905, bij het opstellen van zijn speciale relativiteitstheorie, de knoop doorgehakt en gezegd: ‘Als de natuur zo is, dat er geen ether gemeten kan worden, laten we dan maar aannemen, dat de ether niet bestaat’.

Het relativiteitsprinCipe

Deze theorie van Einstein gaat in de eerste plaats uit van het relativiteitsprincipe: voor elk tweetal waarnemers die ten opzichte van elkaar met een vaste snelheid bewegen hebben alle natuurwetten dezelfde vorm. Het woord speciaal houdt in dat de snelheid van de coördinatenstelsels ten opzichte van elkaar constant is. Pas in de algemene relativiteitstheorie van 1915 ging het ook over coördinatenstelsels die versneld ten opzichte van elkaar bewegen. 

De snelheid van het liCht is voor elke waarnemer Constant

Als tweede principe stelde Einstein dat de snelheid van een lichtstraal voor elke waarnemer even groot is: c = 300 000 km/s, geheel onafhankelijk van de snelheid en richting van de bron van deze lichtstraal.

Einstein had deze veronderstelling nodig om een aantal onopgeloste problemen in de stralingstheorie te kunnen oplossen, die de natuurkunde in het laatste deel van de negentiende eeuw gekweld hadden. Ook hier huldigde Einstein het principe: 'Als de natuur zo is, dat een lichtstraal door elke waarnemer met dezelfde snelheid wordt waargenomen, dan zullen we dat moeten aanvaarden en van daaruit verder rekenen en de resultaten ter bevestiging meten.'

Albert Einstein

Paul Ehrenfest

Maar vreemd was het wel. Lang niet alle natuurkundigen waren bereid om dit principe te aanvaarden. Een van de natuurkundigen die er niet aan wilde, was Walther Ritz (1878-1909). Hij hield vol dat als een ster met snelheid $v$ naar de aarde toe beweegt, en tevens een lichtstraal richting aarde uitstraalt, dat die lichtstraal met een snelheid $c + v$ richting aarde beweegt. En als de ster van de aarde af beweegt, beweegt de lichtstraal met een snelheid $c - v$ naar de aarde.

Het experimentum CruCisvan Paul Ehrenfest

In 1912 stelde de natuurkundige Paul Ehrenfest (1880-1933) in zijn inaugurale rede bij zijn benoeming tot hoogleraar in Leiden het volgende experiment voor. Neem twee lichtbronnen, de één stilstaand ten opzichte van de waarnemer en de ander ernaartoe bewegend. De waarnemer laat de stralen door een pijp met lengte $L$ gaan en meet na elkaar de twee tijden $T_1$ en $T_2$ waarin de twee stralen de pijp passeren. Voor $T_1$ geldt natuurlijk: $T_1 = L/c$. Als Ritz gelijk had, zou
gelden: $T_2 = \frac{L}{(c + v)} < T_1$. Als Einstein gelijk had, zou gelden $T_2 = T_1$. Ehrenfest noemde het een experimentum crucis, een cruciale proefneming. Simpel, zo leek het. Maar de grootte van de lichtsnelheid maakte de te meten tijden voor een laboratoriumexperiment zo klein, dat ze niet gemeten konden worden. De Nederlandse sterrenkundige Willem de Sitter (1872-1934) zat in de zaal toen Ehrenfest zijn voorstel deed en dacht meteen dat lichtstralen van dubbelsterren
wellicht de oplossing konden bieden.

Dubbelsterren als experimentum CruCis

Er zijn twee soorten dubbelsterren: de ene soort is een visuele dubbelster, een waarbij twee sterren die ver van elkaar staan vanuit de aarde gezien vlak naast elkaar liggen. Dat is natuurlijk geen 'echte' dubbelster. Die bedoelde De Sitter niet. De andere soort heet een fysische dubbelster, een met de volgende eigenschap: ze staan dicht bij elkaar (op astronomische schaal natuurlijk) en draaien onder invloed van elkaars zwaartekracht om elkaar heen. Laten we aannemen dat een van de twee sterren een massa heeft die veel groter is dan die van de andere ster. Beide sterren draaien om het gemeenschappelijke zwaartepunt, dat vlak bij het middelpunt van de zware ster ligt. In goede benadering kunnen we dan aannemen dat de lichte ster in een cirkelvormige baan rond de zware ster draait. We laten voor het gemak elliptische banen achterwege. We nemen ook aan dat de baan van de lichte ster en de aarde in één vlak liggen. We zien de lichte ster dus van links naar rechts bewegen en weer terug (soms voor de zware ster langs, soms er achterlangs). De omlooptijd noemen we $T$.

We kunnen aannemen dat de afstand tussen de twee sterren, de straal van de baan $R$, verwaarloosbaar is vergeleken met de afstand tot de aarde $L: R \ll L$.

Wat zien we op aarde als Einstein gelijk heeft?

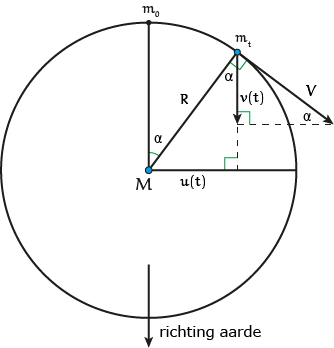
Figuur 1

In de figuur staat de grote ster met massa $M$ in het middelpunt van de cirkelvormige baan en de kleine ster met massa $m$ op de omtrek ($m_0$ op tijdstip $0$, $m_t$ op tijdstip $t$). Dan hebben we

$$\alpha = 2\pi \frac{t}{T}\\V=2\pi\frac{R}{T}$$

Noem $u(t)$ de projectie van de afstand van $m$ tot $M$ op de middellijn van de baan loodrecht op de richting naar de aarde, als functie van de tijd $t$. Noem $v(t)$ de snelheid van $m$ in de richting van de aarde. In een cirkelvormige
baan zien de functies $u(t)$ en $v(t)$ er uit als een sinus:

$$u(t) = R\cdot \sin\left(2\pi\frac{t}{T}\right)$$	$(1)$
$$v(t) = \frac{2\pi R}{T}\sin\left(2\pi\frac{t}{T}\right)$$	$(2)$

Opgave 1

Controleer in de figuur de formules $(1)$ en $(2)$.

Op aarde komt elke lichtstraal die van de ster is vertrokken aan een tijd $L/c$ later. Op aarde zullen we dus weer precies dezelfde grafiek voor $u(t)$ zien, namelijk formule $(1)$: een heel gewone sinus dus.

Nu is het zo dat bij alle waarnemingen van dubbelsterren met genoemde eigenschappen precies deze normale sinus wordt waargenomen. Dat lijkt dus op het gelijk van Einstein. Geen enkele natuurkundige tot die tijd had beseft dat deze gewone sinus van de beweging van een lichte dubbelster om een zware een sterke indicatie was voor het feit dat de lichtsnelheid constant is voor elke waarnemer, onafhankelijk van de snelheid van de bron.

Wat zien we op aarde als Ritz gelijk heeft?

Maar misschien is het voorgaande met Ritz’ veronderstelling ook wel zo. Laten we dat eens precies bekijken. Volgens Ritz is de snelheid $v_R$ van een lichtstraal die uiterst rechts richting aarde vertrekt gelijk aan:

$$v_R=c+v(t)$$

$(3)$

Dat houdt dus in dat de lichtstraal die van de ster vertrekt in het uiterste punt rechts de aarde eerder bereikt dan in het geval dat de lichtsnelheid richting aarde $c$ is. De top van de sinus schuift dus iets naar links (punt $B$ in figuur 2). Als de ster in het punt het dichtst bij de aarde een lichtstraal uitzendt (de snelheid richting aarde is dus $0$), dan is de snelheid van de lichtstraal richting aarde dus $c$ en bereikt die straal de aarde dus op hetzelfde tijdstip als in het geval van Einstein (punt $C$). Dat punt van de sinus op de $t$-as blijft op zijn plaats. Als de ster weer naar links beweegt, dus van de aarde af, is de snelheid van een uitgezonden lichtstraal volgens Ritz dus 

$$v_L=c-v(t)$$

$(4)$

De lichtstraal die vertrekt als de ster helemaal links is, komt dus later bij de aarde, zodat het laagste punt van de sinus naar rechts schuift (punt $D$).

De grafiek wordt dan als in figuur 2:

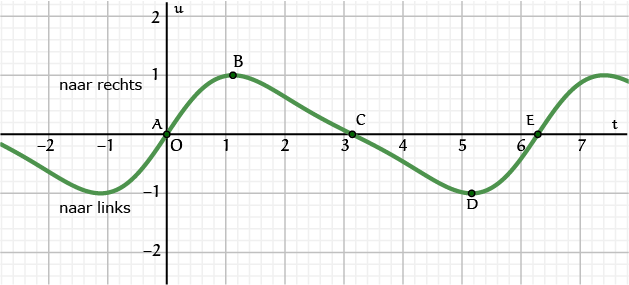
Figuur 2

Deze afwijkende sinussen waren bij de dubbelsterren die De Sitter kende onbekend. Maar het kon nog gekker, zoals De Sitter beweerde.

De liChte ster is tegelijkertijd op meerdere plaatsen zien

Stel dat we een dubbelster hebben met een heel bijzonder aantal waarden $L$, $R$ en $T$. Die waarden volgen uit de volgende beschrijving. Laat een lichtstraal van de lichte ster vertrekken die zich vanuit de aarde gezien in de uiterste stand links bevindt en dus van de aarde af beweegt met de maximale snelheid $v_{max}= 2\pi\frac{R}{T}$. De tijd $T_L$ die deze lichtstraal nodig heeft om de aarde te bereiken is:

$$T_L=\frac{L}{c-v_{max}}$$

$(5)$

Een lichtstraal, die vertrekt na een halve omwenteling (dus $T/2$ later), bereikt de aarde na het vertrek van de eerste lichtstraal na een tijd $T_R$:

$$T_R=\frac{T}{2}+\frac{L}{c+v_{max}}$$

$(6)$

Het bijzonder gekke geval kan zich nu voordoen, dat deze twee lichtstralen tegelijkertijd de aarde bereiken. We zouden de kleine ster dus tegelijkertijd links en rechts zien!

Dus als:

$$\frac{L}{c-v_{max}}=\frac{T}{2}+\frac{L}{c+v_{max}}$$

$(7)$

Of:

$$L\approx\frac{c^2T}{4v_{max}}$$

$(8)$

Opgave 2

Leidt de benaderde formule $(8)$ af.

De diverse fysische grootheden moeten dan wel aan deze relatie voldoen. Dat zal dus vast niet vaak voorkomen, maar uit deze berekening blijkt wel dat er, in het geval Ritz gelijk zou hebben, bij veel dubbelsterren dus kleine tot zeer grote afwijkingen zouden kunnen voorkomen van een gewone sinus. En dat één ster wel eens op meerdere plaatsen tegelijkertijd zichtbaar is.

Ten slotte

Nu zijn er extreem veel dubbelsterren in onze Melkweg: de helft van de 250 miljard sterren maakt deel uit van een dubbelster. Zoveel kende Willem de Sitter er natuurlijk niet. Maar met de gegevens waarover Willem de Sitter wel beschikte, kon hij bevestigen nog nooit een zodanig vervormde grafiek in alle bekende waarnemingen te zijn tegengekomen. Hij kende alleen mooie sinussen in de tijd (en bij ellipsbanen alleen de grafieken die daarbij horen). En dubbelsterren waarvan de één op een enkel tijdstip op aarde op meerdere verschillende punten zichtbaar was, zulke idiote dubbelsterren had Willem de Sitter al helemaal nooit gezien. Hij noemde de theorie van Ritz op zijn eigen bijzondere wijze absurd. Hij zei dat als Ritz gelijk had, maar toch op de aarde een keurige sinus waargenomen werd, de gravitatiewet van Newton ter plekke van de dubbelster wel een heel krankzinnige vorm zou moeten aannemen, en ook nog eens een vorm die varieerde met de afstand van de dubbelster tot de aarde.

De publicatie van Willem de Sitters resultaat deed Einstein veel genoegen. Zijn veronderstelling dat de lichtsnelheid voor elke waarnemer constant is, was nu experimenteel bevestigd.

Relativiteitstheorie Deel 1: Elke waarnemer meet in alle gevallen dezelfde lichtsnelheid Deel 2: Tijddilatatie en trager lopende klokken Deel 3: Gelijktijdigheid en lengtecontractie Deel 4: De som van twee snelheden Deel 5: Bijzondere gekkigheden