We gaan weer uit van een assenstelsel $S$ waarin, net als in het vorige artikel over tijddilatatie, de waarnemer zich bevindt. Een tweede assenstelsel $S'$ beweegt met een snelheid $v$ in de richting van de positieve $x$-as. De $x$-as en de $x'$-as bewegen over elkaar en de oorsprong $O'$ van $S'$ passeert $O$ van $S$ op tijdstip $t = t' = 0$. We beschouwden in het vorige artikel een bijzondere klok in de oorsprong $O'$ van $S'$: een foton bewoog verticaal heen en weer tussen twee spiegeltjes, waar het telkens bij aankomst in $O'$ een 'kloktik' veroorzaakte. In $O'$ van $S'$ hadden we dus een klok geconstrueerd. Als $T'$ het verschil was tussen twee gebeurtenissen in $O'$, werd die tijd in $S$ waargenomen als $T$, met:

$$T=T'\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}.$$

Gelijktijdig is niet altijd gelijktijdig

Er is nog iets bijzonders aan de hand als gevolg van het feit dat een lichtstraal waargenomen wordt door elke waarnemer met een snelheid $c$.

De waarnemer is in rust ten opzichte van coördinatenstelsel $S$. Ten opzichte van $S$ beweegt dus het coördinatenstelsel $S'$ met een snelheid $v$. We gebruiken nu alleen de $x$- en de $x'$-as. In $S'$ plaatsen we twee identieke klokken op afstanden $a$ links en rechts van de oorsprong $O'$, dus in de punten met $x_L = -a$ en $x_R = a$. We willen deze klokken gelijkzetten. Dat doen we door op $t' = 0$ op de klok in de oorsprong $O'$ een kort lichtflitsje te maken. Zie figuur 1.

Figuur 1

Dit stuurt in beide richtingen een lichtfoton uit, naar de twee klokken toe. De klokken staan, voordat de fotonen hen bereiken, stil op tijd $a/c$. Dat hebben we gedaan omdat de fotonen over de afstand van $O'$ naar elk van de twee klokken op $x' = -a$ en $x' = +a$ een tijd $a/c$ doen (tijd is afgelegde weg gedeeld door snelheid). Als de fotonen de klokken bereiken, dus $a/c$ seconden na hun vertrek uit de oorsprong, worden ze direct aangezet. Dan lopen ze verder beide gelijk aan elkaar en ook gelijk met de klok in de oorsprong. Op deze wijze kunnen we op alle punten in het coördinatenstelsel $S'$ klokken gelijkzetten. Stelsel $S'$ beweegt met snelheid $v$ in de $x$-richting ten opzichte van de waarnemer in stelsel $S$. Op $t = t' = 0$ passeert de oorsprong $O'$ van $S'$ de oorsprong $O$ van $S$ (we mogen deze tijdstippen zo kiezen). 

De twee klokken (op $-a$ en $a$ in $S'$) bewegen in $S$ beide met een snelheid $v$ naar rechts. Vanwege de symmetrie neemt de waarnemer in $S$ op $t = 0$ de klokken waar in de punten met $x_L = -b$ en $x_R = b$.

Intermezzo Waarom nemen we nu $b$ en niet $a$? Uitgaande van de constantheid van de lichtsnelheid voor elke waarnemer, zal een waarnemer in $S$ een object, vast in $S'$, anders waarnemen dan die waarnemer in $S'$. Verder in dit artikel zullen we ontdekken dat de waargenomen lengte $2b$, gemeten in $S$, van een bewegende staaf met lengte $2a$ in $S'$, kleiner is dan $2a$. Dan is er sprake van lengtecontractie. Maar dat is nu voor ons niet belangrijk. Wel belangrijk is dat de afstanden in $S'$ tussen $O'$ en de twee klokken door een waarnemer in $S$ vanwege de symmetrie als gelijke afstanden gemeten worden.

We hebben in S voor de plaatsen van de linker en rechter klok $x_{LK}$ en $x_{RK}$ nu

$x_{LK} = -b + v \cdot t$  en $x_{RK} = b + v \cdot t$.

Nu de plaatsen $x_{LF}$ en $x_{RF}$ van de twee fotonen. Deze bewegen ten opzichte van $S$ 'gewoon', zoals het relativistisch hoort, met snelheid $c$:

$x_{LF} = -c \cdot t$ en $x_{RF} = c \cdot t$.

Om de tijdstippen waarop de fotonen de klokken bereiken, $t_L$ en $t_R$ in $S$, te berekenen, stellen we dus: $x_{LK} = x_{LF}$ en $x_{RK} = x_{RF}$.

Opgave 1 Bewijs dat voor $t_L$ en $t_R$ gelden: $t_L = \frac{b}{c+v}$ en $t_R=\frac{b}{c-v}$.

Hieruit volgt direct dat:

$$t_L < t_R.$$

Het foton naar links bereikt in $S$ eerder de linkerklok dan het foton naar rechts de rechterklok bereikt. Gelijktijdig in $S’$ is dus niet altijd gelijktijdig in $S$.

Lengtecontractie

In de vorige paragraaf namen we voor de afstand van de twee klokken tot de oorsprong in $S$ de afstand $b$ en niet $a$. We zullen in het volgende nu aantonen dat $b < a$, dus dat een waarnemer in $S$ de lengte van een voorwerp in $S’$ verkort waarneemt. Er is dan sprake van contractie. 

In het vorige artikel maakten we gebruik van een verticaal staande ‘klok’ in $S’$, die telkens ‘tikte’ als een foton op het spiegeltje in $O’$ botste, telkens na een keer op en neer gegaan te zijn. Er was dus sprake van een klok in $O’$.

In het volgende maken we weer gebruik van deze klok in $O’$ in $S’$, maar nu leggen we hem horizontaal langs de $x’$-as, met het linkereinde in $O’$. We hebben hem alleen over $90^{\rm o}$ gedraaid. Dat is voor een klok in $S’$ natuurlijk geen bezwaar. We nemen nu deze klok in $S’$ in de vorm van een lange buis met lengte $L’$ die horizontaal stil op de $x’$-as ligt en aan beide einden een spiegeltje heeft. Het linker einde bevindt zich op $t’ = 0$ in de oorsprong $O’$. Op $t’ = 0$ laten we een foton daar vertrekken. Dat kaatst heen en weer en geeft telkens in $O’$ een ‘kloktik’.

Figuur 2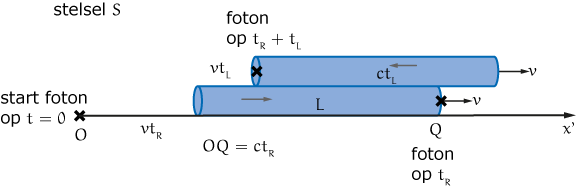

Opnieuw beweegt $S’$ met een constante snelheid $v$ naar rechts ten opzichte van stelsel $S$, waarbij de oorsprong $O’$ de oorsprong $O$ passeert op tijdstip $t = t’ = 0$. Het foton bereikt op $t’$ het spiegeltje aan het rechtereinde, met:

$$L’ = ct’.$$

Daar kaatst het terug en bereikt $O’$ weer in dezelfde tijd $t’$, in totaal dus in $2L’/c$ seconden. Dat is allemaal rechttoe rechtaan. Laten we nu bekijken hoe een waarnemer $W$ in stelsel $S$ dit ziet.

De lange buis wordt in $S$ waargenomen met een lengte $L$. De lengte $L$ is in $S$ te bepalen door op hetzelfde tijdstip in $S$ de $x$-coördinaten te meten van de uiteinden van de buis (de klokken in $S$ zijn overal allemaal gesynchroniseerd). Er hoeft niet te gelden dat $L = L’$. Het zou kunnen, maar in de relativiteitstheorie moeten we voorzichtig zijn. Het foton dat vertrekt in $O = O’$ op $t = t’ =0$ bereikt op tijdstip $t_R$ het spiegeltje rechts en legt dus een afstand $ct_R$ af. Het heeft in ieder geval de lengte van de buis $L$ afgelegd. Maar het rechtereinde is naar rechts bewogen over een afstand $vt_R$. Er geldt dus (van het kruisje links tot het kruisje rechts in figuur 2):

$$ct_R = L + vt_R.$$

Dan de terugweg opnieuw naar het begin van de buis. In de figuur is de buis voor de duidelijkheid iets hoger getekend. Het foton bereikt het begin van de buis na een tijd $t_L$. Maar het zal niet de volledige lengte $L$ afleggen, omdat het linkereinde het foton tegemoetkomt over een afstand $vt_L$. Er geldt dan (van het kruisje rechts naar het middelste kruisje in figuur 2): 

$$ct_L = L - vt_L.$$

De totale tijd die het foton in $S$ erover gedaan heeft om heen en weer te gaan is $t_R + t_L$.

Opgave 2 Leidt uit de voorgaande formules af dat: $$t_R+t_L=\frac{2L}{c}\cdot\frac{1}{1-\frac{v^2}{c^2}}.$$

In het stelsel $S’$ was die tijd:

$$2t=\frac{2L}{c}.$$

Nu weten we uit het vorige artikel dat er bij deze twee tijden sprake is van tijddilatatie. Dus er geldt:

$$t_R+t_L=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\cdot 2t'.$$

Opgave 3 Leid uit de voorgaande formules het volgende verband tussen $L$ en $L'$ af: $$L=\sqrt{1-\frac{v^2}{c^2}}L'.$$

Aangezien de factor voor $L’$ kleiner is dan $1$, geldt $L < L’$. De waarnemer in $S$ neemt de bewegende buis dus korter waar dan de waarnemer $W’$ in stelsel $S$, waarin de buis stil staat. Er is sprake van verkorting of lengtecontractie.

Opgave 4 Als een voorwerp met lengte $L'$ in $S'$ wordt waargenomen in $S$ met een contactie van $20\%$ (dus $L=4/5L'$), met welke snelheid $v$ in km/s beweegt $S'$ zich dan ten opzichte van $S$?.

 

De formule voor de lengtecontractie, ook wel Lorentzcontractie genaamd, op een muur in Leiden

Relativiteitstheorie 4

In het volgende artikel zullen we ons afvragen wat de som is van twee snelheden. Als een trein langsrijdt met een snelheid van $10$ m/s ten opzichte van een stilstaande waarnemer op het perron, en als in de trein een passagier naar voren
wandelt met een snelheid van $2$ m/s ten opzichte van de trein, met welke snelheid zal de waarnemer op het perron deze wandelaar dan zien passeren? Normaal is dat natuurlijk $10$ m/s + $2$ m/s = $12$ m/s. Maar als je nu heel grote snelheden neemt, bijvoorbeeld $3/4c$ en $3/4c$, dan zou je op $3/2c > c$ uitkomen, maar dat mag niet in de speciale relativiteitstheorie. Welke formule moeten we dan nemen om altijd onder de lichtsnelheid $c$ te blijven?

Relativiteitstheorie Deel 1: Elke waarnemer meet in alle gevallen dezelfde lichtsnelheid Deel 2: Tijddilatatie en trager lopende klokken Deel 3: Gelijktijdigheid en lengtecontractie Deel 4: De som van twee snelheden Deel 5: Bijzondere gekkigheden