Normaal is dat natuurlijk de som van de twee snelheden:$10 m/s + 2 m/s = 12 m/s$. Maar als je nu heel grote snelheden neemt, bijvoorbeeld ${}^3\!/\!{}_4c$ en ${}^3\!/\!{}_4c$ ($c$ is de lichtsnelheid), dan zou je op ${}^3\!/\!{}_2c > c$ uitkomen, maar dat mag niet in de speciale relativiteitstheorie. Welke formule moeten we dan nemen om altijd onder de lichtsnelheid $c$ te blijven?

Een lichtstraal ontmoet een bal

We bekijken dat aan de hand van een waarnemer die stil staat op een perron, in de oorsprong van een coördinatenstelsel $S$. De $x$-as loopt langs de spoorrails en de positieve richting is naar rechts. Hij ziet een treinwagon naar rechts passeren met lengte $L^\prime$ in het eigen coördinatenstelsel $S^\prime$. De snelheid gemeten in $S$ is $v$. De linkerkant van deze wagon bevindt zich in de oorsprong $O^\prime$ van $S^\prime$ en passeert op $t = t^\prime = 0$ de oorsprong $O$. Op $t^\prime = 0$ beginnen een lichtfoton en een bal in de wagon naar rechts te bewegen, het foton uiteraard met een snelheid $c$ en de bal met een snelheid $u$. Zie figuur 1.

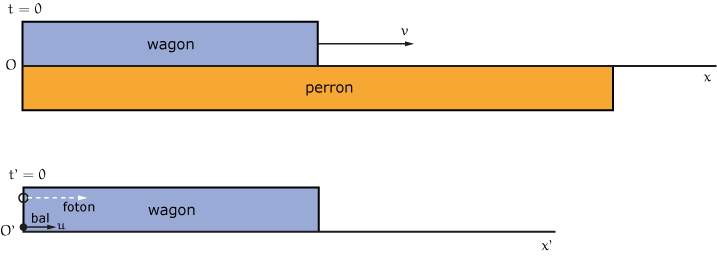
De waarnemer op het perron ziet de bal ten opzichte van het perron (stelsel $S$) bewegen met een snelheid $w$. We willen nu een formule vinden die $w$ uitdrukt in $v$ en $u$. Aan de voorkant van de wagon zit een spiegel
waarop het foton terugkaatst. De bal gaat natuurlijk langzamer en beweegt dan nog naar rechts. Op een zeker tijdstip ontmoeten de bal en het foton elkaar.

Ontmoeting in S’

We gaan nu in $S^\prime$ uitrekenen waar en wanneer deze ontmoeting plaatsvindt. We schetsen eerst de situatie in de wagon in figuur 2.

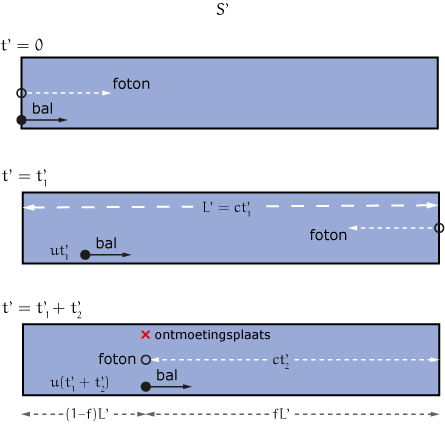
De tijd waarop het foton de spiegel bereikt, is $$t^\prime_2=\frac{L^\prime}{c}.$$ Noem $t^\prime_2$ de tijd die het foton erover doet om van de spiegel aan de voorkant van de wagon terug te keren en de bal te ontmoeten. De bal heeft vanaf de oorsprong een tijd $t^\prime_1+t^\prime_2$ gebruikt tot de plaats van ontmoeting. Dan geldt dus:
$$L^\prime=u(t^\prime_1+t^\prime_2)+ct^\prime_2.$$

Opgave 1 Elimineer $t^\prime_1$ met de eerste vergelijking uit de tweede en toon aan dat: $$t^\prime_2=\frac{c-u}{c+u}\cdot\frac{L^\prime}{c}.$$

Het punt P waarop bal en foton elkaar ontmoeten, verdeelt $L^\prime$ rechts en links in twee gedeeltes, $f$ en $(1 - f)$, met $f + (1 - f) = 1$. Voor fractie $f$ krijgen we dan:

$$f=\frac{ct^\prime_2}{L^\prime}=\frac{c-u}{c+u}.$$

Ontmoeting in S

Laten we nu de ontmoeting van bal en foton bekijken in het stelsel $S$ (zoals gezien door de waarnemer op het perron) in figuur 3.

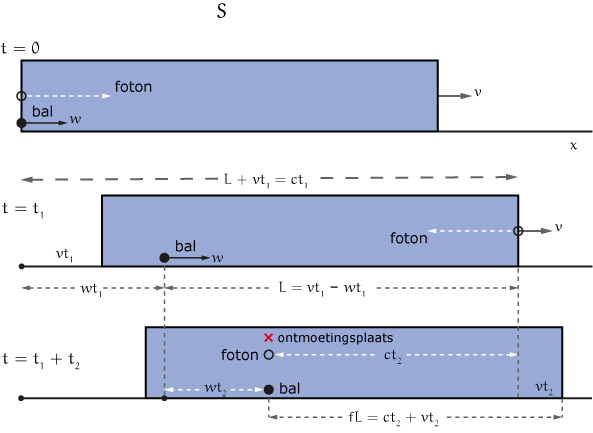
Het foton bereikt de spiegel aan de voorkant van de wagon op tijdstip $t_1$, waarbij het een afstand $ct_1$ aflegt. Echter, de voorkant van de trein is in die tijd een stukje vooruitgereden ter grootte van $vt_1$. Dan geldt dus:

$ct_1=L+vt_1$   ofwel:   $t_1=\frac{L}{c-v}$.

In de teller staat nu $L$ in plaats van $L^\prime$, omdat we meten in stelsel $S$ van het perron. We weten dat door lengtecontractie $L < L^\prime$. Nu gaan we $t_2$ berekenen, de tijd die het foton vanaf de spiegel nodig heeft om de bal te ontmoeten. Als het foton vanaf de spiegel start, heeft de voorkant van de wagon in $t_1$ een afstand afgelegd van $vt_1$ en de bal een afstand van $wt_1$. De afstand tussen foton en bal in S op dat tijdstip is dan $L + vt_1 - wt_1$. De bal, gaande naar rechts, en het foton, gaande naar links, ontmoeten elkaar na $t_2$. Ze leggen dan de afstand $wt_2 + ct_2$ af. Dan geldt:

$$L+vt_1-wt_1=wt_2+ct_2.$$

Opgave 2 Bereken $t_2$ uit de laatste twee vergelijkingen: $$t_2=\frac{L}{c-v}\cdot\frac{c-w}{c+2}.$$

Plaats van ontmoeting

Het punt van ontmoeting van foton en bal in de wagon kan in de wagon worden aangegeven met een kruis op de bodem. Dat kruis verdeelt in $S^\prime$ de wagon, zoals we al gezien hebben, in twee delen: $fL^\prime$ en $(1 - f)L^\prime$.

Voor de waarnemer op het perron is de lengte $L^\prime$ verkort tot $L$, maar de twee stukken waarin de stip de lengte $L$ van de wagon verdeelt, zijn precies evenveel verkort. Voor die twee delen geldt dus $fL$ en $(1 - f)L$, met dezelfde waarde van $f$. Het stuk $fL$ is dus de afstand tussen het kruis en het einde van de wagon. Dus:

$$fL=ct_2+vt_2.$$

De relativistische som van twee snelheden

Als we $t_2$ van de voorlaatste vergelijking invullen in de laatste, krijgen we voor $f$:

$$f=\frac{c-w}{c+w}\cdot\frac{c+w}{c-v}.$$

Ten slotte kunnen we de twee uitdrukkingen voor $f$ aan elkaar gelijkstellen (de uitdrukking hierboven en die op de vorige bladzijde):

$$\frac{c-w}{c+w}\cdot\frac{c+v}{c-v}=\frac{c-u}{c+u}.$$

Dit is het gezochte verband tussen de snelheid $w$ (van de bal in $S$), uitgedrukt in de twee snelheden $v$ (van de wagon in $S$) en $u$ (van de bal in de wagon).

Opgave 3 Los $w$ op uit de laatste vergelijking: $$w=\frac{u+v}{1+\frac{uv}{c^2}}.$$

Hiermee hebben we de formule voor $w$ gevonden. Als voorbeeld kunnen we de twee grote snelheden $v = {}^3\!/\!{}_4c$ en $u = {}^3\!/\!{}_4c$ nemen. Dan krijgen we door invullen $w = 24/25c$. Dus nog net onder de lichtsnelheid, terwijl de som $3/2$ keer de lichtsnelheid is. Hoe dicht we ook de twee snelheden $u$ en $v$ bij de lichtsnelheid $c$ nemen, de somformule geeft altijd een snelheid kleiner dan $c$. Als we in de limiet twee keer de lichtsnelheid nemen, dan krijgen voor de som:

$$w=\frac{c+c}{1+\frac{c^2}{c^2}}=c.$$

Slotartikel Relativiteitstheorie 5

In het slotartikel van deze serie zullen we een paar bijzondere toepassingen bekijken. Een daarvan is het antwoord op de vraag: hoe zie ik een kubus die met zeer grote snelheid over mij heen suist? We zullen ontdekken dat we de kubus geroteerd zien, en dus niet alleen maar verkort. Dat heeft te maken met het feit dat een voorwerp zien betekent dat lichtstralen van dat voorwerp tegelijkertijd mijn oog bereiken.

Relativiteitstheorie Deel 1: Elke waarnemer meet in alle gevallen dezelfde lichtsnelheid Deel 2: Tijddilatatie en trager lopende klokken Deel 3: Gelijktijdigheid en lengtecontractie Deel 4: De som van twee snelheden Deel 5: Bijzondere gekkigheden