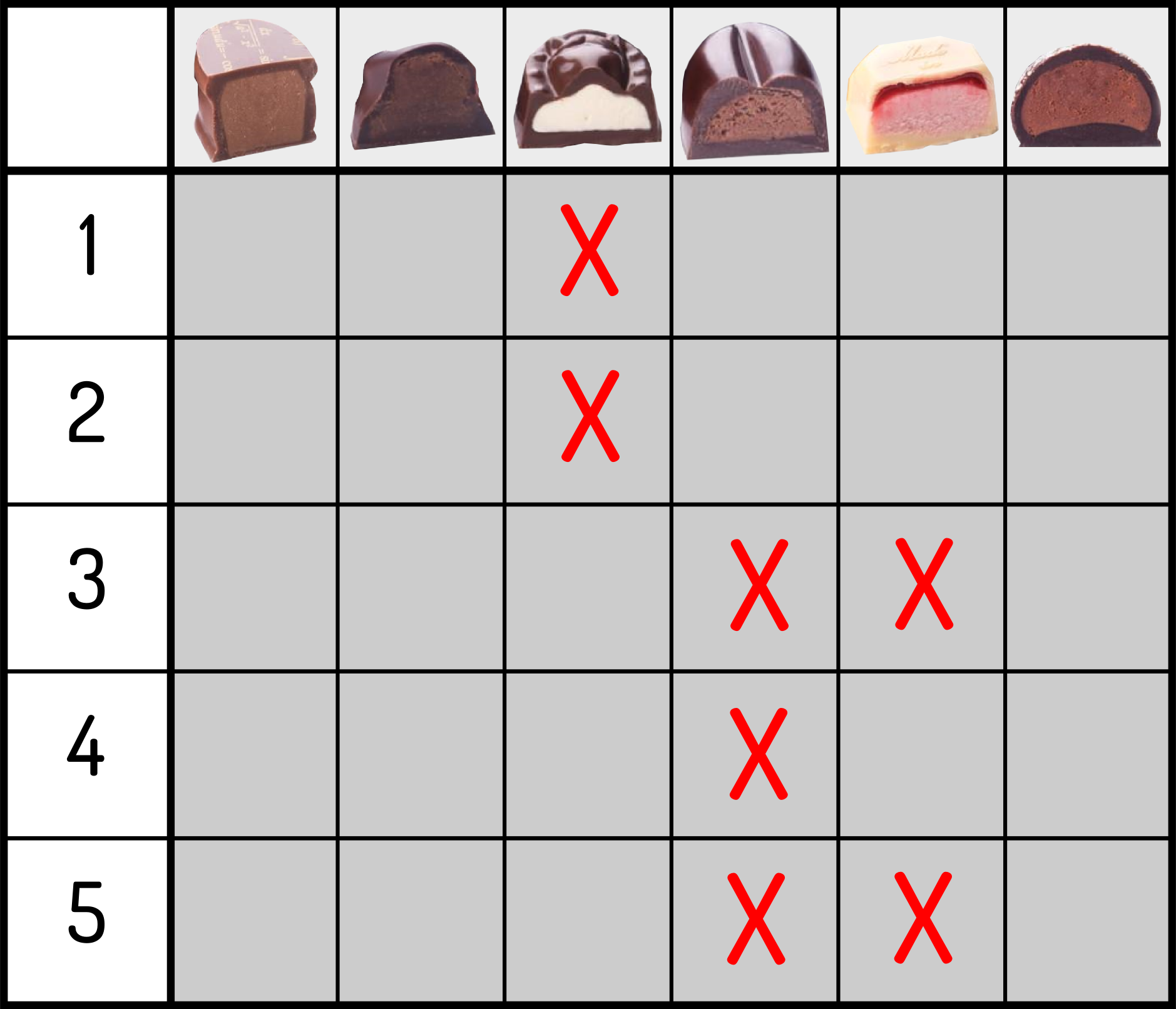
Probeer het even: zoek hiernaast dus naar een manier om uit elk groepje $1$ kaart te selecteren zodat we uiteindelijk één kaart voor elk van de $13$ waarden hebben. Kleuren (schoppen, klaveren, ruiten en harten) hebben geen belang. In dit geval lukt het. Je ziet een oplossing van het probleem rechts. Schud nu zelf de $52$ kaarten, verdeel ze opnieuw in $13$ groepen, en probeer het nog eens. Lukt het? Als het niet lukt, zoek dan nog even verder, want dankzij een stelling uit de wiskunde zijn we er zeker van dat het altijd kan! Een ander voorbeeld Ik krijg wel eens een doos pralines cadeau. Maar zoals dat ook bij vele andere mensen het geval is, heb ik niet alle pralines even graag. Gelukkig zijn er dan familieleden die ook pralines lusten en een andere smaak hebben dan ik. Laat ons even veronderstellen dat er nog $6$ pralines over zijn in de doos, allemaal verschillende smaken. We zijn met vijf thuis en ik laat iedereen een lijstje maken met daarop de pralines die zij lusten. De vraag is dan: is het altijd mogelijk om iedereen (minstens) één praline te geven die op zijn of haar lijstje staat? In figuur 1 zie je een mogelijk lijstje voorkeuren. Links staan mijn familieleden, die we voor de eenvoud geen naam maar een nummer hebben gegeven. In dit geval kunnen we elk familielid een praline van haar/zijn lijstje geven. Zie je hoe? Er zijn meerdere oplossingen. Merk op dat we per rij één kruisje (= praline) willen en dat alle gekozen kruisjes in verschillende kolommen moeten staan.

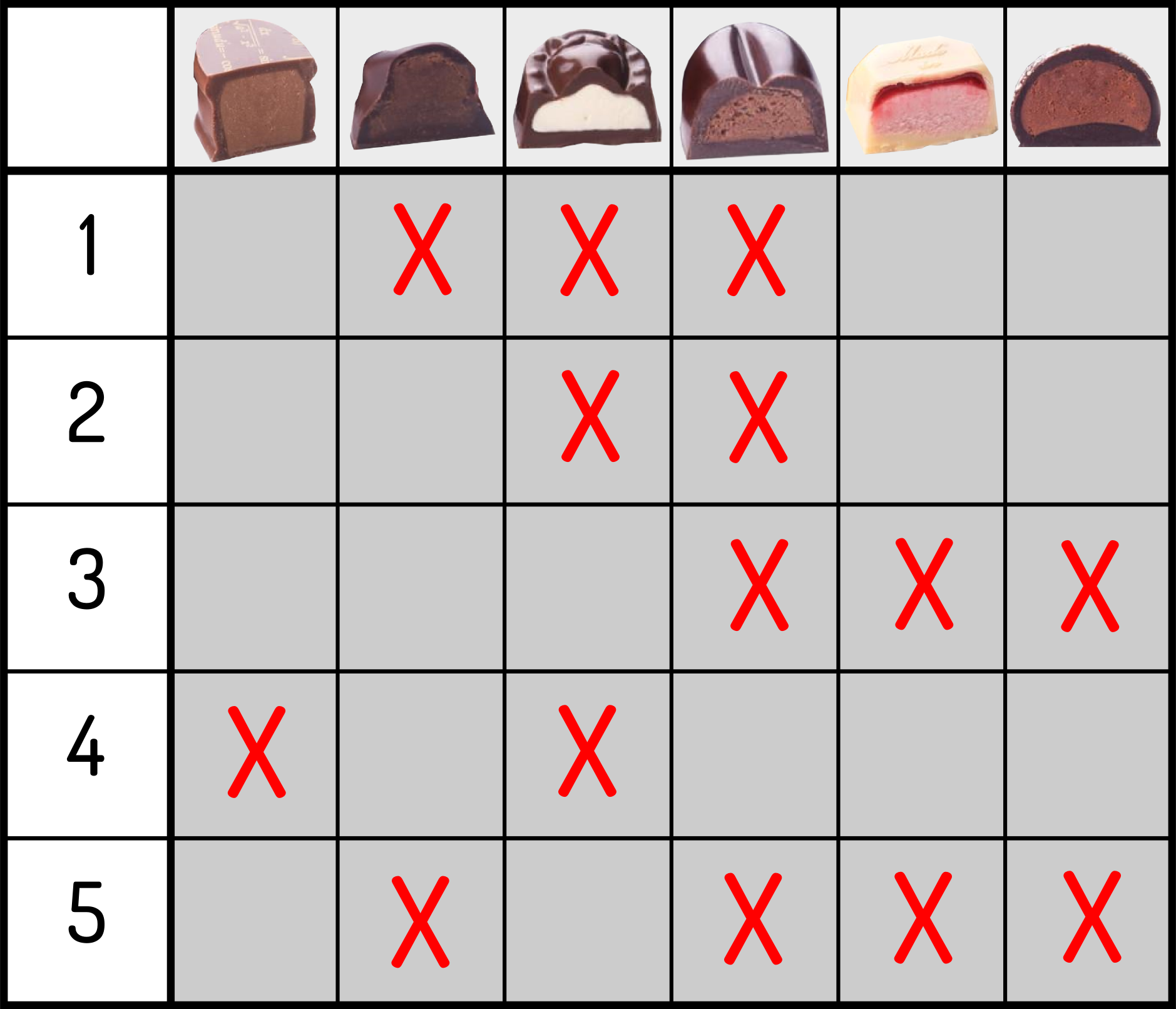
Soms, als je een kieskeurige familie hebt, gaat het duidelijk mis, zoals in figuur 2.

Als je de keuze van familieleden 1 en 2 bekijkt, dan zie je dat ze allebei maar $1$ soort praline lusten, en omdat het toevallig dezelfde is, en er van elke soort praline maar eentje is, is het natuurlijk onmogelijk om in dit geval ieders keuze te volgen. Als je kijkt naar de keuze van familieleden 3, 4 en 5 dan zie je een gelijkaardig probleem: in hun keuze zitten in totaal maar $2$ verschillende pralines, en omdat ze met $3$ zijn, zal het nooit lukken. We zetten even deze zaken op een rijtje, en generaliseren:

• Als eender welke twee familieleden maar $1$ praline in hun voorkeurslijstje hebben staan, en het is voor beiden dezelfde praline, dan is er geen oplossing (1 en 2 in figuur 2).
• Als in de voorkeurslijstjes van eender welke drie familieleden samen minder dan $3$ verschillende pralines zitten, dan is er geen oplossing (3, 4 en 5 in figuur 2).
• Meer algemeen: als je de voorkeurslijstjes van eender welke $4$ familieleden samenlegt, en je merkt dat er $3$ of minder verschillende pralines in voorkomen, dan is er geen oplossing. En ook: als je de lijstjes van alle $5$ de familieleden samenlegt en je hebt minder dan $5$ verschillende pralines, dan is er geen oplossing.

Dat is natuurlijk erg logisch: het zijn allemaal gevallen waarin het duidelijk niet zal lukken. Maar wanneer lukt het dan zeker wel? Dat is precies wat de huwelijksstelling van Hall ons zegt: indien we in geen van de vorige gevallen zitten, dan is er zeker een oplossing!

Stelling van Hall

Een noodzakelijke en voldoende voorwaarde voor het bestaan van een oplossing is, dat elke groep van $k$ (met $k \ge 1)$ familieleden samen ten minste $k$ verschillende pralines in hun voorkeurslijstje hebben staan.

Deze stelling, die dateert uit 1935, bracht een omwenteling teweeg in het deel van de wiskunde dat met eindige verzamelingen bezig is.

Ga zelf na dat er in figuur 1 inderdaad aan deze voorwaarden voldaan is. Hoeveel combinaties van familieleden moet je dan controleren?

Terug naar de speelkaarten

En hoe zit het dan bij de truc met de speelkaarten? We maken een overzicht zoals in het vorige voorbeeld. De rol van de familieleden wordt gespeeld door de $13$ groepjes met $4$ willekeurige kaarten, de verschillende pralines worden vervangen door de dertien verschillende waarden die kaarten kunnen hebben. In figuur 3 staan links de groepjes kaarten, en in elke rij geven we aan welke waarden voorkomen in het groepje links.

In dit geval is het aantal groepjes precies gelijk aan het aantal verschillende waarden die speelkaarten hebben, namelijk $13.$ De vraag is dus of we uit elk groepje kaarten één kaart kunnen kiezen op zo'n manier dat de $13$ gekozen kaarten de $13$ verschillende waarden hebben, of nog: kunnen we in elke rij een vinkje kiezen zodat al die vinkjes in verschillende kolommen staan? In figuur 4 zie je de oplossing van het voorbeeld in het begin.

Wat zegt de stelling van Hall in dit geval? Is er voldaan aan de voorwaarden? Aangepast aan dit geval moeten we het volgende nagaan: als we willekeurig $k$ (met $k \ge 1)$ van de groepjes van vier kaarten nemen, zitten er dan steeds ten minste $k$ kaarten met verschillende waarden bij? Het antwoord is overduidelijk ja. Het geval $k = 1$ hoeft geen uitleg. Neem bijvoorbeeld $k = 2:$ bevatten $2$ groepjes van $4$ kaarten minstens $2$ kaarten met een verschillende waarde? Natuurlijk wel: er zijn in een kaartspel telkens maar $4$ kaarten met dezelfde waarde, en we hebben $2$ maal $4$ is $8$ kaarten. Op dezelfde manier geldt het ook voor andere waarden van $k:$ je hebt dan namelijk $4k$ kaarten, dus minstens $k$ verschillende waarden.

De stelling van Hall garandeert ons dan het bestaan van een oplossing!

Uitbreiding

We kunnen zelfs nog verder gaan. Indien we de $13$ gekozen kaarten verwijderen, dan blijven er nog $13$ groepjes van $3$ kaarten over. Hiermee kunnen we precies hetzelfde doen: we kunnen in elk groepje van $3$ een kaart kiezen op zo'n manier dat we (opnieuw) $13$ kaarten met verschillende waarden hebben (oranje in figuur 5). En met de $13$ groepjes van $2$ lukt dat ook (blauw in figuur 5). Ga zelf na dat er in deze gevallen opnieuw voldaan is aan de voorwaarden van de stelling van Hall.

Meer over de huwelijksstelling van Hall (onder andere waarom deze stelling zo genoemd wordt) kan je lezen in het gelijknamige artikel van Dion Gijswijt dat in Pythagoras 48‑3 (januari 2009) is verschenen.

Paul Levrie en Rudi Penne zijn beide werkzaam aan de Universiteit Antwerpen.