De opgave C1 Een aap zit in de top $P_0$ van een heel hoge gelijkbenige driehoek met tophoek a en met een horizontale basis. Hij maakt steeds even grote sprongen, waarbij hij om en om landt op de linkerzijde en de rechterzijde van de driehoek. Hij springt nooit terug naar zijn vorige positie, maar altijd naar een positie die verder van $P_0$ ligt dan de vorige positie op die zijde. Als dat niet meer lukt, dan stopt hij met springen. De punten waarop de aap achtereenvolgens neerkomt, noemen we $P_1, P_2, \dots, P_n$. Hiernaast zie je twee voorbeelden voor $n = 4$. Stel de aap springt vier keer ($n = 4$) en de laatste sprong is horizontaal, oftewel $|P_0 P_3| = |P_0 P_4|$. Bereken de tophoek van de driehoek. Stel de tophoek van de driehoek is 6 graden. Hoe vaak kan de aap dan maximaal springen? (De driehoek is zo hoog dat hij de grond nooit bereikt.)

Op het eerste gezicht lijkt deze opgave erg abstract. Er zijn weinig lengtes of hoeken gegeven om op te bouwen en de route van de aap verandert ook nog eens voor elke verschillende driehoek die je tekent. Vaak is het in zo'n geval, als je eigenlijk niet weet waar je moet beginnen, handig om gewoon maar iets te proberen en te kijken of je een vermoeden kunt krijgen van wat je wilt bewijzen. Zo'n vermoeden is bij de Wiskunde Olympiade vaak al een groot deel van je antwoord en het maakt de rest van het bewijs een stuk makkelijker.

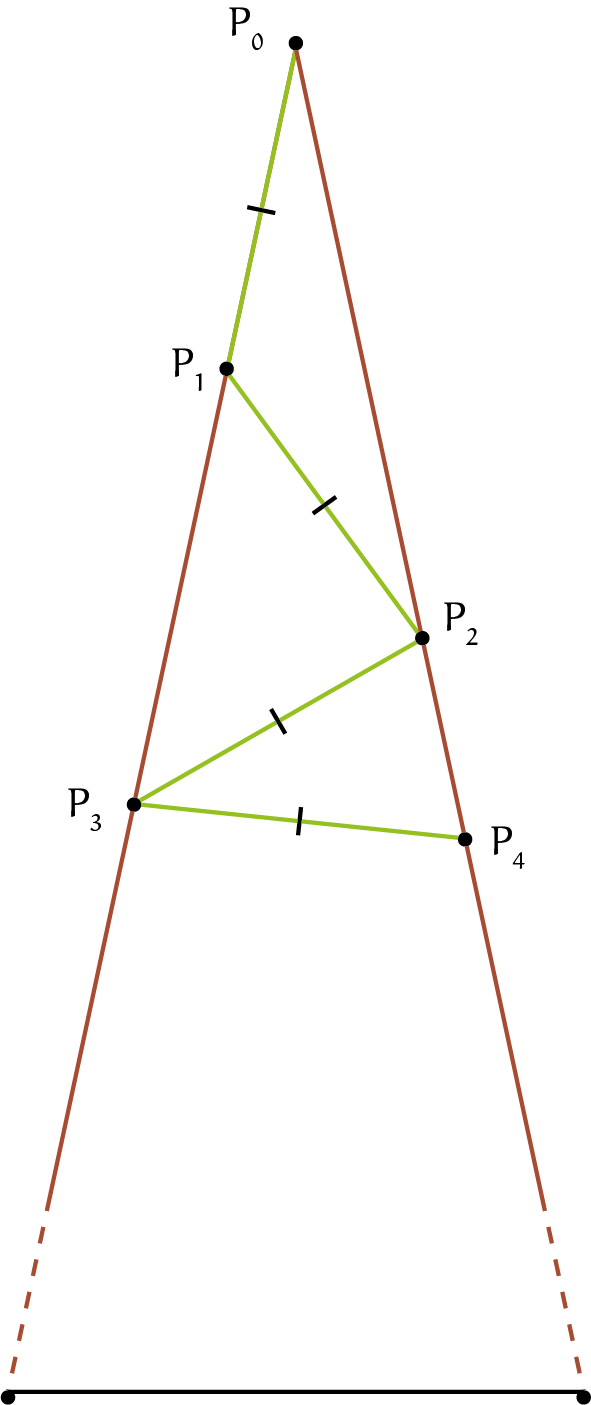
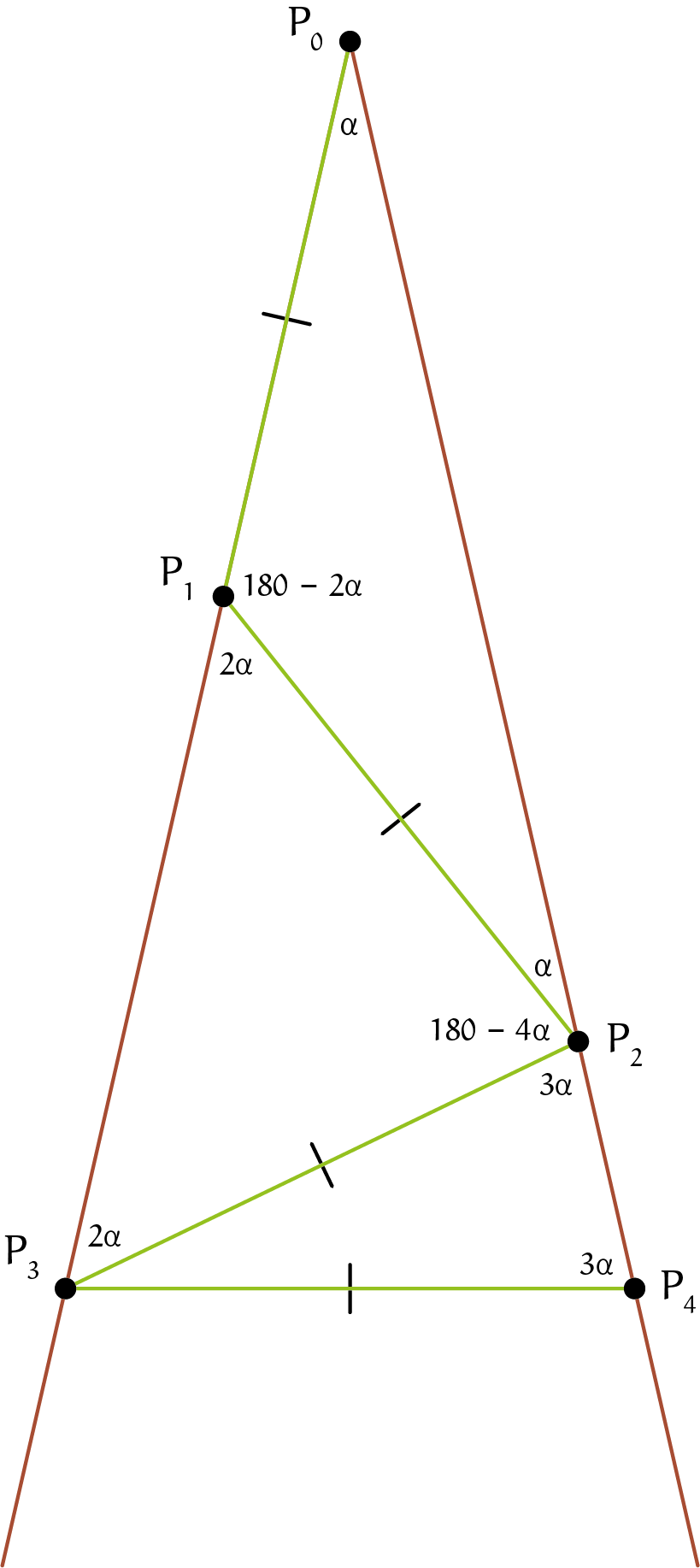
Laten we beginnen met kijken naar de eerste aar sprongen van de aap. Hij springt als eerste van $P_0$ naar $P_1$, langs de linkerzijde van de driehoek. Vervolgens springt hij van $P_1$ naar $P_2$ op de andere zijde van de driehoek en daarna van $P_2$ naar $P_3$, waarbij hij weer terugkomt op de zijde waar $P_1$ ook op ligt. In de opgave is gegeven dat elke sprong van de aap even lang is, dus we weten dat $|P_0 P_1| = |P_1 P_2| = |P_2 P_3|$, etc.

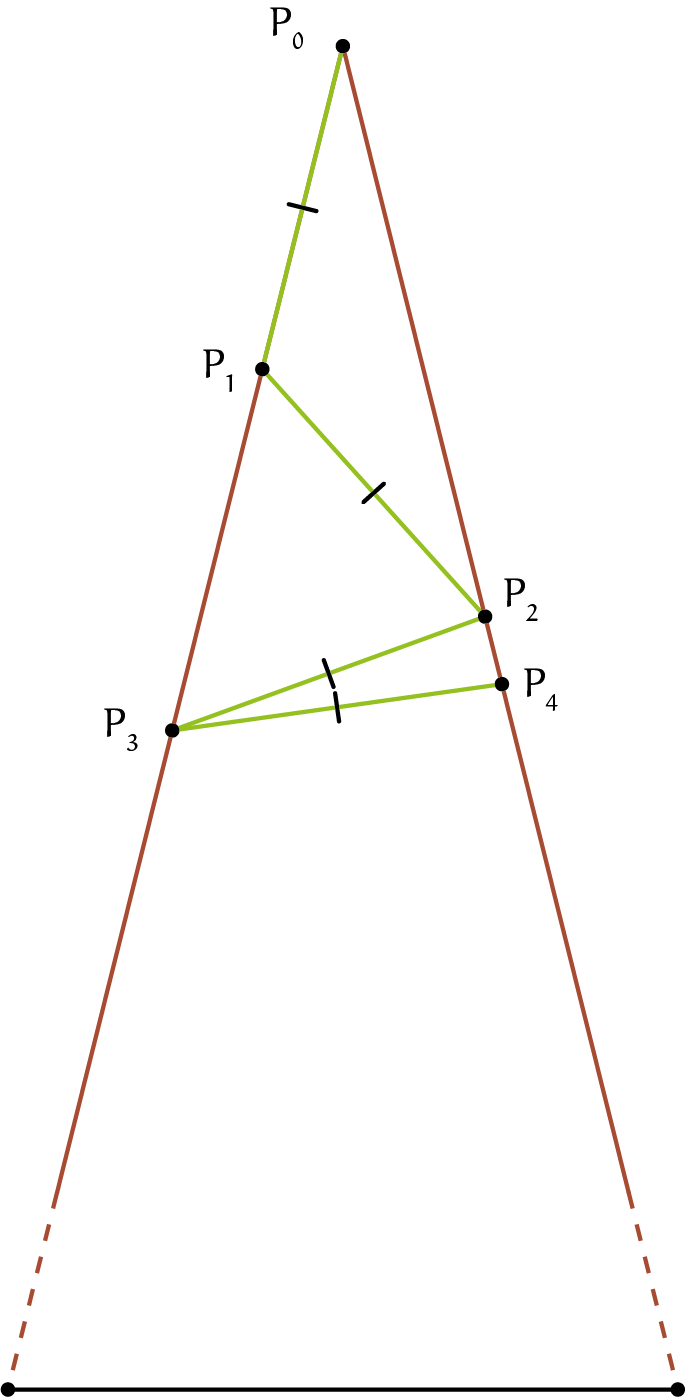
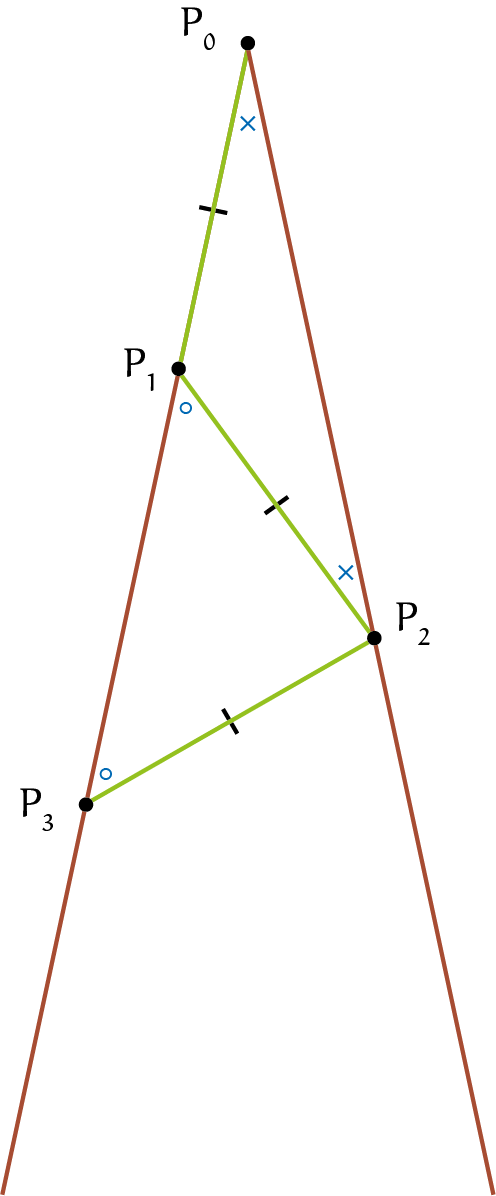
Nu we dit weten, kunnen we iets zeggen over de patronen die de aap maakt tijdens het springen. Elke driehoek die de aap maakt door twee keer te springen, is namelijk gelijkbenig. Zo is driehoek $P_0P_1P_2$ gelijkbenig met tophoek $\angle P_0P_1P_2$ omdat $|P_0 P_1| = |P_1 P_2|$. Net zo is driehoek $P_1P_2P_3$ gelijkbenig met tophoek $\angle P_1P_2P_3$ omdat $|P_1 P_2| = |P_2 P_3|$ en is elke volgende driehoek die de aap creëert door heen en weer te springen ook gelijkbenig (zie figuur 1). Dit is nuttig, want dit helpt met het berekenen van de hoeken die de aap maakt tijdens het springen.

Als er geen hoeken gegeven zijn, zoals bij deze opgave, komt het bij meetkundeopgaven vaak van pas om een hoek te benoemen, en daarmee verder te rekenen. Op die manier kun je de andere hoeken in deze benoemde hoek uitdrukken, wat erg handig is voor het bewijzen van bepaalde eigenschappen, zoals gelijkvormigheid. Het namen geven van bepaalde dingen die je vaak gebruikt in je bewijs kan je ook nog eens helpen om je bewijs overzichtelijk te houden. Dubbel handig dus! 

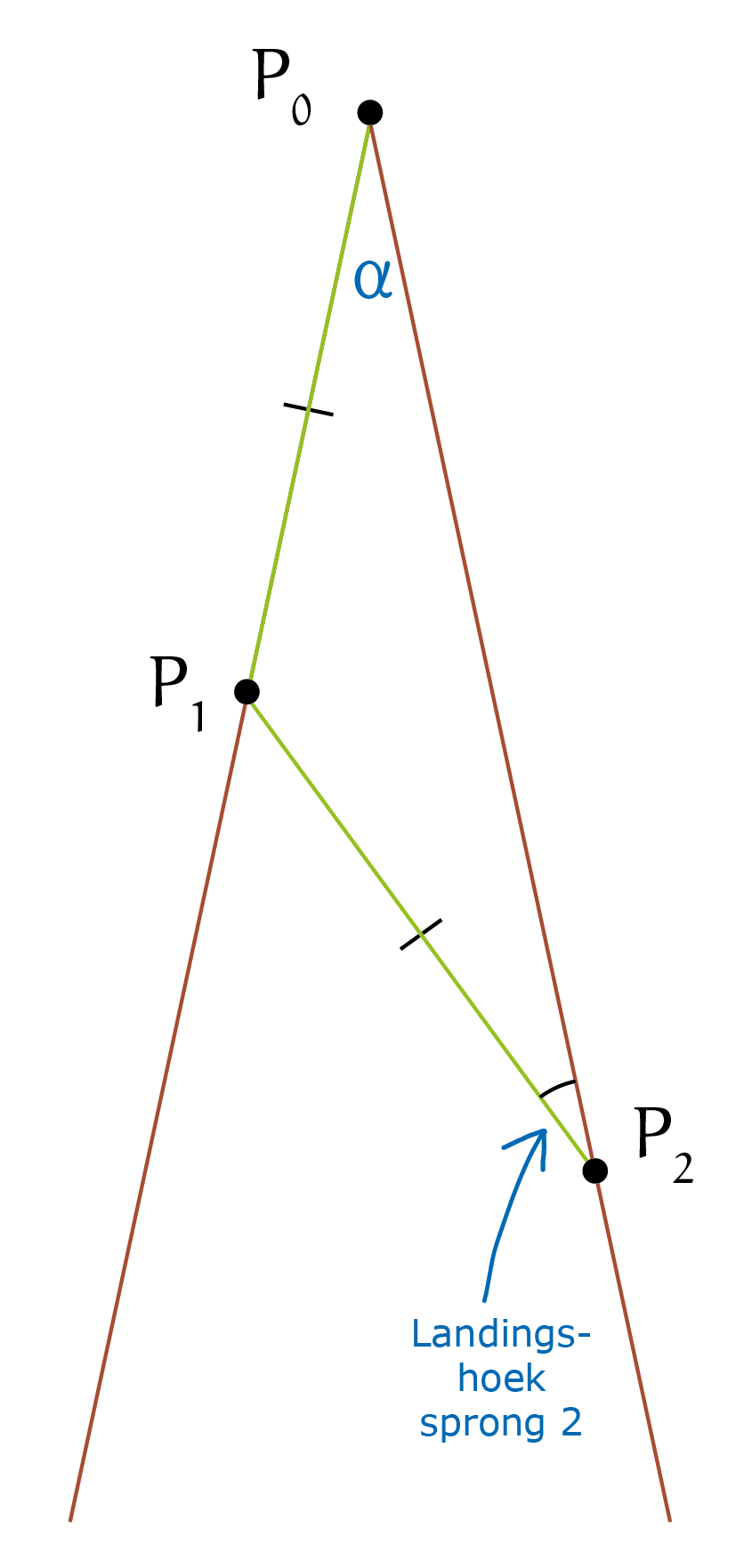
In de opgave is het benoemen van deze hoek al voor ons gedaan: de tophoek van de grote driehoek, $\angle P_1P_0P_2$, is $\alpha$ . Daarnaast noemen we de hoek tussen de spronglijn van de aap en het lijnstuk van $P_0$ naar het punt waarop de aap landt, de landingshoek. De landingshoek na sprong $n$ noteren we met $\angle L_n$, dus $\angle L_n = \angle P_{n-1}P_nP_0$. Zo is $\angle L_2= \angle P_1P_2P_0$, en is $\angle L_{16} = \angle P_{15}P_{16}P_0 (= \angle P_{15}P_{16}P_{14})$. Nu we een beter beeld hebben van hoe de aap precies springt, kunnen we de opgaven gaan oplossen: zie figuur 2.

Twee keer heen en weer

Voor onderdeel (A) willen we weten wat de tophoek van de driehoek is als de vierde sprong van de aap horizontaal is. Laten we kijken naar de eerste vier sprongen van een aap in een driehoek met tophoek $\alpha$ en kijken of we daarmee verder komen: $\angle L_1 = 0^{\rm o}$ en $\angle L_2 = \angle P_1P_2P_0$ , maar dit is gelijk aan de tophoek van de grote driehoek, omdat driehoek $P_0P_1P_2$ gelijkbenig is met tophoek $\angle P_0P_1P_2$. De landingshoek na zijn tweede sprong is dus $\angle L_2 = \angle P_1P_2P_0 = \angle P_1P_0P_2 = \alpha$.

Omdat $\angle P_1P_2P_0 = \angle P_1P_0P_2 = \alpha$, weten we door de hoekensom van de driehoek dat: $\angle P_0P_1P_2 = 180^{\rm o} -2\alpha$. Door de gestrekte hoek bij $P_1$ weten we dan dat $\angle P_2P_1P_3 = 180^{\rm o} - \angle P_0P_1P_2 = 180^{\rm o}-(180^{\rm o}-2\alpha)=2\alpha$. Driehoek $P_1P_2P_3$ is gelijkbenig met tophoek $\angle P_1P_2P_3$, dus $\angle L_3=\angle P_2P_3P_0 = \angle P_2P_3P_1=\angle P_2P_1P_3=2\alpha$. Hieruit volgt door de hoekensom van driehoek $P_1P_2P_3$ weer dat $\angle P_1P_2P_3 = 180^{\rm o} - \angle P_2P_1P_3-\angle P_2P_3P_1 = 180-4\alpha$. Door de gestrekte hoek bij $P_2$ weten we dat $\angle P_3P_2P_4=180^{\rm o} - \angle P_1P_2P_0 - \angle P_1P_2P_3 = 180^{\rm o} - \alpha - (180^{\rm o} - 4\alpha) = 3\alpha$. Driehoek $P_2P_3P_4$ is gelijkbenig met tophoek $\angle P_2P_3P_4$, dus $\angle L_4 =\angle P_3P_4P_0 = \angle P_3P_4P_2 = \angle P_3P_2P_4 =  3\alpha$.

Dit lijkt misschien weinig te zeggen, maar eigenlijk zijn we nu al heel dicht bij de oplossing! In de opgave staat dat de vierde sprong van de aap horizontaal is, dat wil zeggen dat $|P_0 P_3| = |P_0 P_4|$. Dit betekent dat driehoek $P_3P_0P_4$ gelijkbenig is, met tophoek $\angle P_3P_0P_4$. Maar deze tophoek is gelijk aan hoek $\angle P_1P_0P_2$, dus $\angle P_3P_0P_4 = \alpha$. Omdat driehoek $P_3P_0P_4$ gelijkbenig is met tophoek $\angle P_3P_0P_4$, zijn $\angle P_0P_3P_4$ en $\angle P_0P_4P_3$ gelijk en geldt dat $\angle P_0P_4P_3 = \tfrac{1}{2}\left(180^{\rm o} - \angle P_3P_0P_4\right) = 90^{\rm o} - \tfrac{1}{2}\alpha$. Verder geldt dat $\angle P_0P_4P_3 = \angle P_3P_4P_2$, en we hadden eerder al gevonden dat $\angle P_3P_4P_2 = 3\alpha$. We hebben dus twee verschillende uitdrukkingen voor $\angle P_3P_4P_2$. Als we deze twee uitdrukkingen gelijkstellen zien we dat: $90^{\rm o}-\tfrac{1}{2}\alpha=3\alpha$, dus $3\tfrac{1}{2}\alpha = 90^{\rm o}$ en $\alpha = {\tfrac{180}{7}}^{\rm o}$. In de opgave wordt gevraagd naar de tophoek van de driehoek, en die is $\alpha$. De tophoek van de grote driehoek is dus ${\tfrac{180}{7}}^{\rm o}$, waarmee we antwoord hebben op onderdeel (A).

Blijf doorspringen

Voor onderdeel (B) moeten we berekenen hoe vaak de aap kan springen als de tophoek $6^{\rm o}$ is. Dit kunnen we uittekenen en berekenen, maar je zult snel merken dat dat erg veel tijd en precisie gaat kosten, waarnaast het ook nog eens geen sluitend bewijs is. Vaak is het bij de Wiskunde Olympiade zo dat een eerste, makkelijkere opgave je een vermoeden geeft voor een tweede, moeilijkere opgave, waarin je dit vermoeden kan toepassen. Laten we eens kijken of we zo'n vermoeden kunnen krijgen.

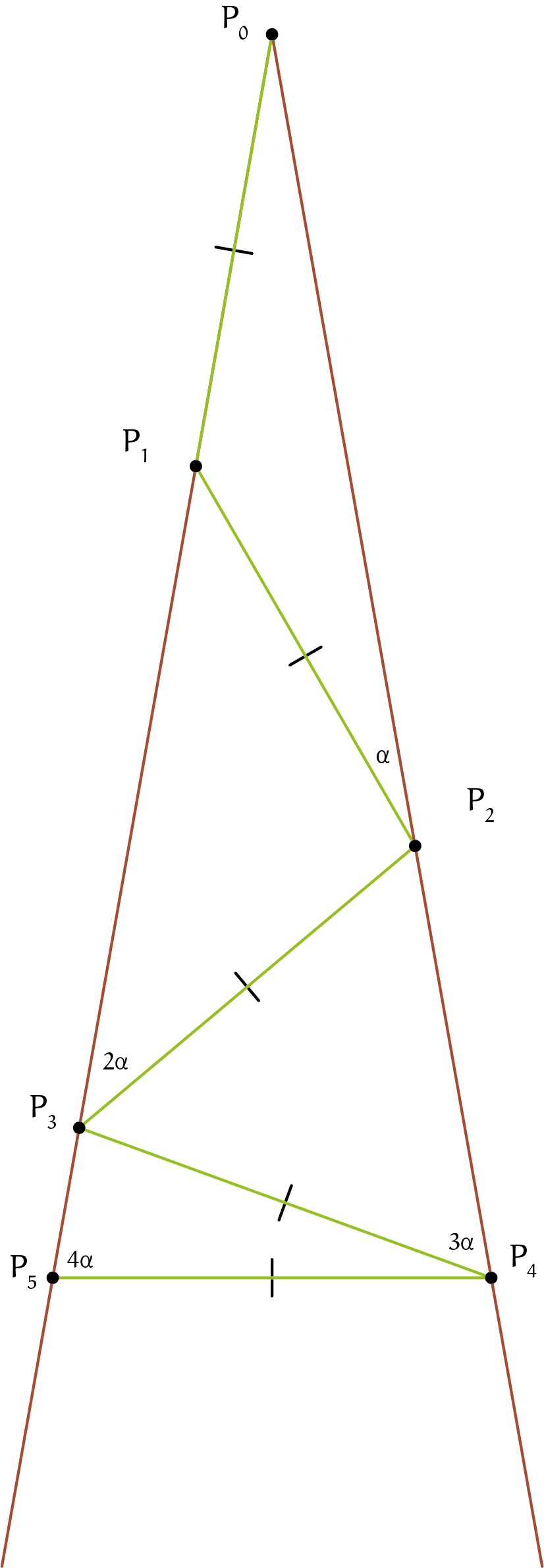
We zagen hierboven al dat $\angle L_2 = \alpha$, $\angle L_3 = 2\alpha$ en $\angle L_4 = 3\alpha$. Analoog vinden we dat $\angle L_5 = 180^{\rm o}- 2\alpha- (180^{\rm o}-6\alpha) = 4\alpha$. Zijn landingshoek lijkt dus na elke sprong precies $\alpha$ groter te worden! Om een volgende landingshoek te berekenen gebruiken we steeds dezelfde redenering: $\angle L_{n+1}$ is namelijk steeds gelijk aan $180^{\rm o}-\angle L_{n-1}-(180^{\rm o}-2\angle L_n)$, oftewel $\angle L_{n+1} = 2\angle L_n - \angle L_{n-1}$. Als we deze formule gebruiken zien we dat:

	$\angle L_6$	$=$	$2\angle L_5 - \angle L_4$	$=$	$8\alpha - 3\alpha$	$=$	$5\alpha$.
	$\angle L_7$	$=$	$2\angle L_6 - \angle L_5$	$=$	$10\alpha - 4\alpha$	$=$	$6\alpha$.
	$\angle L_8$	$=$	$2\angle L_7 - \angle L_6$	$=$	$12\alpha - 5\alpha$	$=$	$7\alpha$.

We zien dus dat dit patroon zich voortzet en dat $\angle L$ steeds $\alpha$ groter wordt! Dit betekent dat we een formule voor $\angle L_n$ kunnen opstellen, namelijk:

$$\angle L_n = (n-1)\alpha.$$

Merk op dat deze inderdaad aan onze formule $\angle L_{n+1}=2\angle L_n-\angle L_{n-1}$ voldoet. Nu we dit weten, kunnen we de opgave gaan beantwoorden.

In de opgave staat dat de aap verder kan springen zolang hij op een punt kan landen dat verder van $P_0$ af ligt dan zijn vorige punt op die zijde. Alle sprongen van de aap zijn even lang, dus de aap kan verder springen zolang hij hierbij een gelijkbenige driehoek creëert, waarbij zijn laatste punt verder van P0 afligt dan zijn andere punt op die zijde. Hiervoor moet gelden dat de landingshoek van de aap kleiner is dan $90^{\rm o}$, omdat hij anders alleen maar boven zijn vorige punt kan neerkomen, of terug kan springen naar zijn vorige positie, wat allebei niet mag. We kunnen dus concluderen dat de aap door kan springen zolang zijn landingshoek kleiner is dan $90^{\rm o}$.

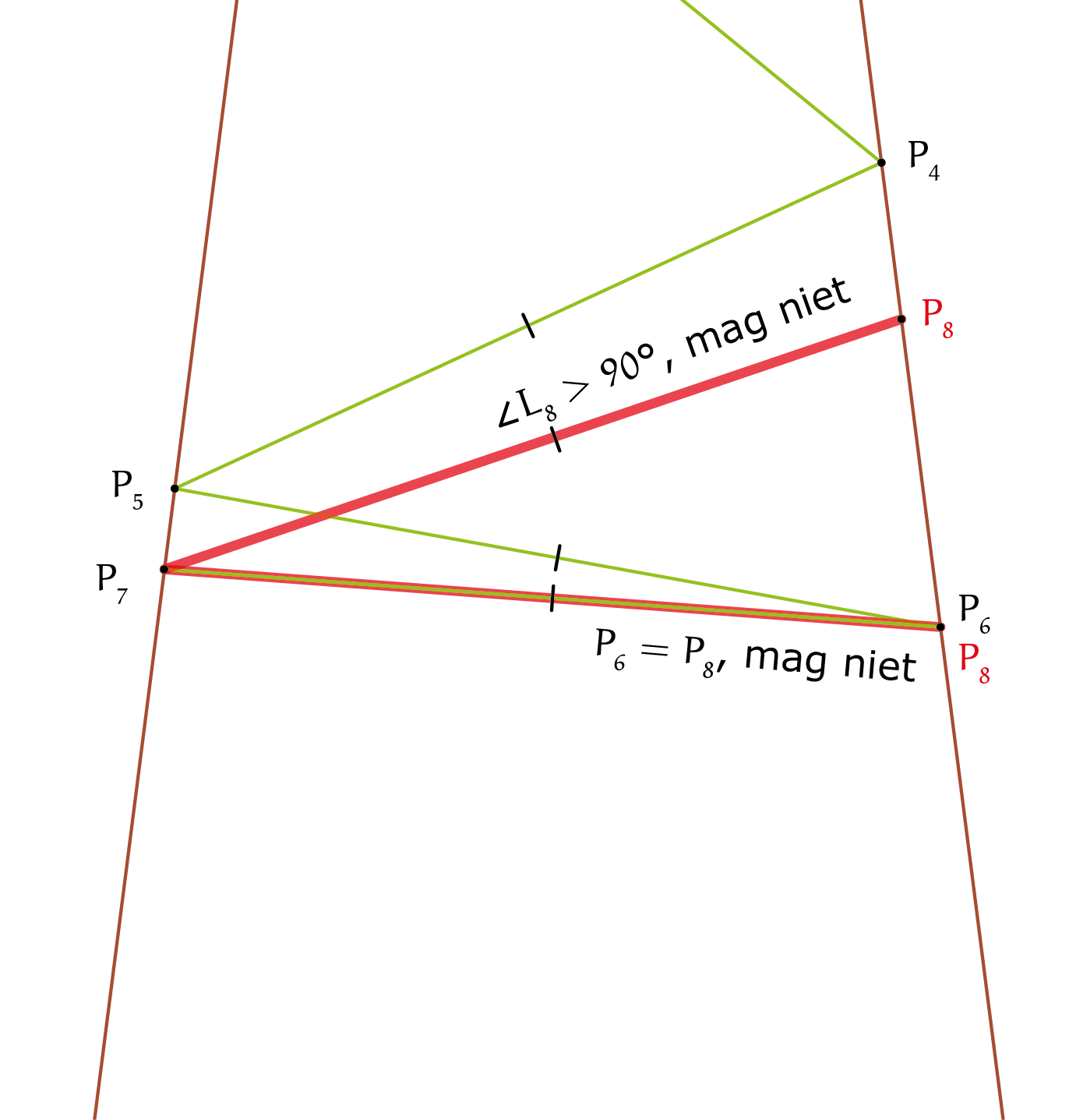
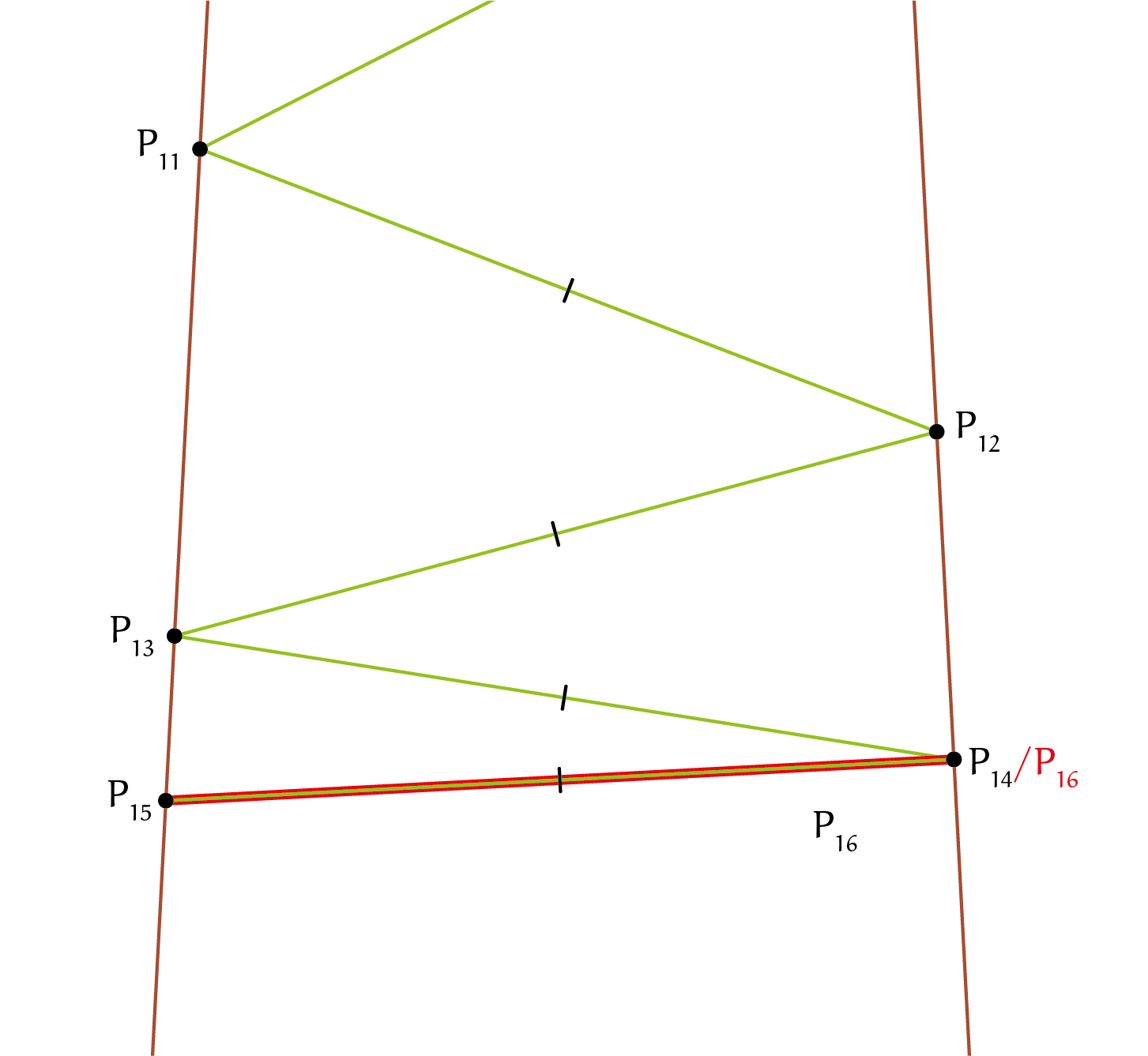
We weten dat de tophoek van de grote driehoek $6^{\rm o}$ is. Als we $\alpha = 6^{\rm o}$ invullen in de formule die we voor $\angle L_n$ hebben gevonden, zien we dat $\angle L_n = (n-1) \times 6^{\rm o}$ . De landingshoek moet kleiner zijn dan $90^{\rm o}$, omdat de aap anders op of boven zijn vorige punt op die zijde neerkomt, wat niet mag. De aap kan dus verder springen zolang $(n - 1)6^{\rm o} < 90^{\rm o}$. Nu is $\angle L_{15} = (15-1) \times 6^{\rm o} = 84^{\rm o}$. Dat betekent dat de aap na zijn zestiende sprong, waarbij hij op $P_{16}$ terechtkomt, niet verder van $P_0$ landt dan zijn vorige positie op die zijde, $P_{14}$; hij komt namelijk precies op $P_{14}$ neer. Dit betekent dat de aap op $P_{15}$ stopt met springen, en dus maximaal $15$ sprongen kan maken bij een tophoek van $6^{\rm o}$, waarmee we het antwoord hebben op de vraag!

Terugblik

Om bij deze opgave tot een oplossing te komen hebben we verschillende strategieën gebruikt. We begonnen met het verduidelijken 
van de opgave, door bepaalde concepten uit de opgave te benoemen. Vervolgens keken we naar de eerste paar sprongen van de aap om erachter te komen wat er gebeurde na elke sprong van de aap. In de wiskunde heten dit de kleine gevallen, en ze komen vaak van pas om ingewikkelde opgaven als deze beter te begrijpen.

Door vervolgens de vermoedens die we kregen tijdens de kleine gevallen te bewijzen en deze te gebruiken om de opgave op te lossen, hebben we het antwoord berekend, en ook nog eens bewezen dat onze oplossing klopt, een sluitend bewijs dus! Zo zie je dat je je, met genoeg geduld en slimme trucjes, zelfs door opgaven die op het eerste gezicht heel moeilijk en abstract lijken, heen kan slingeren.