Tweede ronde Nederlandse Wiskunde Olympiade 2018, opgave B5: Een zaagtandgetal is een positief geheel getal met de volgende eigenschap: van elk drietal cijfers naast elkaar is het middelste cijfer ófwel groter dan zijn twee buurcijfers ófwel kleiner dan zijn twee buurcijfers. De getallen $352723$ en $314$ zijn bijvoorbeeld zaagtandgetallen, maar $3422$ en $1243$ niet. Hoeveel zaagtandgetallen van acht cijfers lang zijn er waarvan elk cijfer een $1,$ een $2$ of een $3$ is?

Deze opgave kregen de deelnemers in de tweede ronde voor hun kiezen. Bij deze opgave hoefde alleen een getal als antwoord gegeven te worden, geen berekening of redenering, maar dat was hier al moeilijk genoeg. Want hoe tel je zaagtandgetallen?

Eerst maar eens kijken wat voor getallen dit eigenlijk zijn. Bijvoorbeeld $12121212$ voldoet aan alle voorwaarden. Echter, lang niet alle zaagtandgetallen zijn zo mooi regelmatig, want $13231213$ voldoet bijvoorbeeld ook. Het is niet zo duidelijk wat nu de structuur van een zaagtandgetal is: blijkbaar is het mogelijk een zaagtandgetal zonder het cijfer $3$ te maken, maar ook eentje met drie keer het cijfer $1,$ twee keer het cijfer $2$ en drie keer het cijfer $3.$ Het is wel mogelijk te tellen hoeveel gewone getallen van acht cijfers lang er alleen de cijfers $1, 2$ en $3$ bevatten. Je maakt namelijk voor elk van de acht posities een keuze uit drie cijfers, dus dat kan op $3^8 = 6561$ manieren. Maar dit zijn lang niet allemaal zaagtandgetallen. Je mag bijvoorbeeld nooit twee dezelfde cijfers naast elkaar hebben. Het lukt misschien nog wel om een handige manier te verzinnen om de getallen met twee dezelfde cijfers naast elkaar uit te sluiten. Maar dan ben je er nog niet, want ook het rijtje $123$ mag bijvoorbeeld niet in het getal voorkomen.

Het uitschrijven van alle $6561$ mogelijkheden en dan afstrepen welke er geen zaagtandgetal zijn, is natuurlijk niet haalbaar. En zelfs met wat handigheidjes lijkt het tellen van de zaagtandgetallen een gigantische klus te worden, met ook nog veel kans op foutjes, terwijl bij deze opgave alleen het antwoord telt, dus één rekenfout en je bent alle punten kwijt. Er moet een slimmere manier zijn om dit te doen. Een tactiek die bij opgaven van de Wiskunde Olympiade vaker van pas komt, is de opgave eerst maar eens wat kleiner maken. Zaagtandgetallen van slechts een paar cijfers zijn prima te tellen.

Zo zijn er $3$ zaagtandgetallen van één cijfer lang, namelijk $1, 2$ en $3.$ De zaagtandgetallen van twee cijfers lang zijn ook makkelijk: $12, 13, 21, 23, 31, 32,$ dus $6$ stuks in totaal. Met drie cijfers lang lukt het ook nog wel: $121, 131, 132, 212, 213, 231, 232, 312, 313, 323,$ in totaal $10.$ Het valt al meteen op dat de makkelijkste manier om de zaagtandgetallen van drie cijfers lang te maken, is om die van twee cijfers lang te nemen en te kijken wat er achter kan staan. Soms kunnen er twee verschillende cijfers achter, soms maar eentje. Om precies te zijn kon er achter $12$ en $32$ maar één cijfer: doordat in $12$ het tweede cijfer groter is dan het eerste, moet er iets kleiners achter en dat moet dan wel weer een $1$ zijn. Evenzo moet er achter $32$ een cijfer groter dan $2,$ dus dat moet wel een $3$ zijn. Bij bijvoorbeeld $23$ zijn er twee mogelijkheden, want zowel $1$ als $2$ zijn kleiner dan $3,$ dus die passen allebei.

Nu wordt het al veel makkelijker om de zaagtandgetallen van vier cijfers lang te maken. Even goed kijken wanneer er maar één cijfer achter een driecijferig zaagtandgetal past: dat is bij $132, 212, 232$ en $312.$ Bij de rest kunnen er twee verschillende cijfers achter. Totaal vinden we nu $4 \cdot 1 + 6 \cdot 2 = 16$ zaagtandgetallen van vier cijfers lang. En elke keer eindigt het getal waar maar één cijfer achter past, op een $2.$ Logisch, want na een $1$ moet altijd een groter cijfer en dan maakt het niet uit of het $2$ of $3$ is; na een $3$ maakt het niet uit of er $1$ of $2$ komt; maar na een $2$ moet er ofwel een groter cijfer (dan wordt het een $3)$ of een kleiner cijfer (dan wordt het een $1).$ Dat ligt al vast, dus na een $2$ is er altijd maar één optie. Dat betekent dat het handig is om bij te houden hoeveel zaagtandgetallen er op een $2$ eindigen. Met vier cijfers zijn dat precies de driecijferige getallen die op een $1$ of een $3$ eindigden en waar een $2$ achter is gekomen; dat waren er $6.$

Tijd om notatie in te voeren. We schrijven $a_n$ voor het aantal zaagtandgetallen van $n$ cijfers lang die op een $1$ of $3$ eindigen en $b_n$ voor het aantal zaagtandgetallen van $n$ cijfers lang die op een $2$ eindigen. We weten nu bijvoorbeeld $a_4 = 10$ en $b_4 = 6.$ Wil je nu een zaagtandgetal van vijf cijfers maken dat op een $2$ eindigt, dan moet je daarvoor een zaagtandgetal van vier cijfers nemen dat op een $1$ of $3$ eindigt en daar een $2$ achter zetten. Dus $b_5 = a_4{:}$ er zijn evenveel zaagtandgetallen van vijf cijfers die op een $2$ eindigen, als zaagtandgetallen van vier cijfers die op een $1$ of $3$ eindigen. En algemener: $b_{n+1} = a_n.$ Hoe maken we nu zaagtandgetallen die op een $1$ of $3$ eindigen? Daarvoor kun je een zaagtandgetal van één cijfer korter nemen dat op een $1$ of $3$ eindigt en er dan een $3$ of $1$ achter zetten, of je neemt een zaagtandgetal dat op een $2$ eindigt en zet er een $1$ of $3$ achter (slechts één van beide cijfers is toegestaan). In formulevorm wordt dit $a_{n+1} = a_n + b_n.$ Deze formule werkt trouwens alleen als $n \ge 2;$ zie je waar in de redenering het mis gaat als $n = 1?$

We hebben nu recursieve formules voor $a_n$ en $b_n{:}$ dat wil zeggen dat je de volgende kunt uitrekenen als je de vorige weet. Met een tabelletje kunnen we nu heel makkelijk verder rekenen:

Het antwoord op de opgave over zaagtandgetallen is dus $68 + 42 = 110.$

Er zijn meer wiskundige problemen waarbij je dit soort recursieve formules tegenkomt. Stel bijvoorbeeld dat je een tegelpaadje wilt aanleggen van $80$ cm breed en $4$ meter lang. Je hebt hiervoor tegels van $40$ bij $80$ cm. Nu zijn er meerdere manieren om dit paadje aan te leggen. Je kunt de tegels namelijk over de breedte van het pad neerleggen, of juist in de lengterichting en dan steeds twee naast elkaar. Een combinatie is natuurlijk ook mogelijk: een voorbeeld zie je in de figuur hieronder.

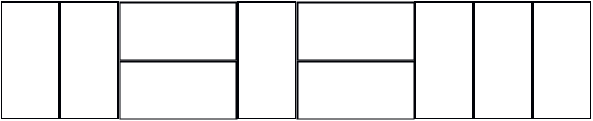
Dus er zijn $89$ mogelijkheden voor het paadje van $4$ meter lang. (Misschien zie je wel een verband tussen de getallen $c_n$ en de getallen $a_n + b_n$ die we hiervoor hadden. Dat is geen toeval! Een leuke uitdaging voor de echte puzzelaar om uit te vogelen waarom dit zo is.)

Een laatste voorbeeld gaat over het verven van een trap. Stel dat je je trap van $7$ treden wat op wilt fleuren door elke trede geel, groen of roze te verven. Maar je wilt geen twee roze treden achter elkaar. Verder is alles goed, dus een volledig gele trap mag bijvoorbeeld ook. Hoeveel mogelijkheden zijn er om je trap te verven?

We kunnen dit vergelijkbaar met de zaagtandgetallen aanpakken. Noem $d_n$ het aantal mogelijkheden voor een trap van $n$ treden waarbij de bovenste trede geel of groen is, en noem $e_n$ het aantal mogelijkheden voor een trap van $n$ treden waarbij de bovenste trede roze is. Als je nu een trap wilt met $n + 1$ treden waarvan de bovenste geel of groen is, dan neem je een willekeurige trap met $n$ treden en verf je de extra trede geel of groen; dat mag altijd allebei. Dus $d_{n+1} = 2d_n + 2e_n.$ Als de bovenste trede roze moet worden, dan mag de trede daarvoor niet roze zijn, dus neem je een trap met $n$ treden waarvan de bovenste geel of groen is en verf je de extra trede roze. Zo vind je $e_{n+1} = d_n.$ Met $d_1 = 2$ en $e_1 = 1$ krijgen we nu:

Dus er zijn $896 + 328 = 1224$ manieren om een trap van $7$ treden te verven.

Het leuke is dat je dit ook op de manier van de tegelpaadjes had kunnen doen. Als je een trap van $n + 2$ treden wil verven en je wilt de bovenste trede roze hebben, dan kun je uitgaan van een trap van $n$ treden, vervolgens trede $n + 1$ geel of groen verven (dat mag allebei) en daarna trede $n + 2$ roze. Als je de bovenste trede geel of groen wilt verven, dan neem je een trap van $n + 1$ treden en verf je trede $n + 2$ geel of groen (dat mag dan ook altijd allebei). Schrijven we dus $f_n$ voor het aantal mogelijke trappen van $n$ treden, dan vinden we $f_{n+2} = 2f_n + 2f_{n+1}.$ Met de hand tellen we dat $f_1 = 3$ en $f_2 = 8$ en dan kunnen we weer verder rekenen:

Er zijn dus twee verschillende manieren om recursieve formules te maken bij het probleem van de traptreden. Natuurlijk komt er hetzelfde antwoord uit, want we tellen dezelfde trappen. Dit kun je overigens ook met alleen het manipuleren van de formules laten zien. Probeer het zelf maar: neem de formules $d_{n+1} = 2d_n + 2e_n$ en $e_{n+1} = d_n$ en probeer hiermee af te leiden dat de som $f_n = d_n + e_n$ voldoet aan $f_{n+2} = 2f_n + 2f_{n+1}.$