De ‘echt rechte’ weg zou $6 \mbox{ km}$ lang moeten worden en $120 \mbox{ cm}$ breed. 

De vraag die we hier bekijken is hoe hoog de uiteinden van de weg boven het aardoppervlak zouden komen te liggen. In de berichten op het web werd vermeld dat dat zo’n $70\mbox{ cm}$ zou zijn; hoe men aan die hoogte is gekomen vermeldt de website niet, misschien door GPS-apparatuur te gebruiken. Je hebt voor een berekening echter niet veel meer nodig dan de stelling van Pythagoras. 

Het plaatje in figuur 1 laat een helft van de weg zien, $3000\mbox{ m}$ vanaf het midden. 

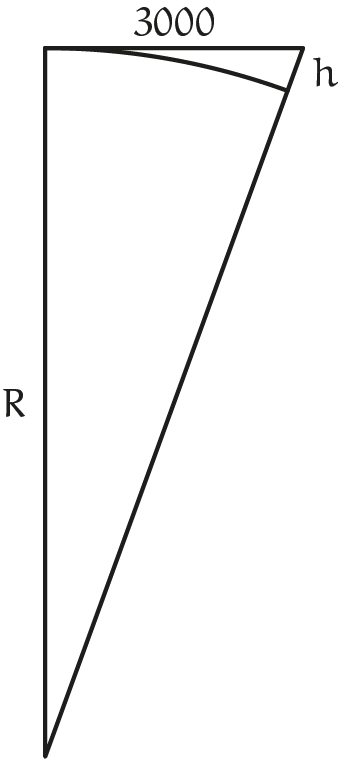
Figuur 1

Hierin is $R$ de straal van de aarde en $h$ de hoogte van het uiteinde. In dit artikel gebruiken we de officiële definitie van de kilometer, waardoor de omtrek van de aarde gelijk is aan $40.000\mbox{ km}$. De straal $R$ is dus 
gelijk aan

$$\frac{40.000}{2\pi}\mbox{ km.}$$

We kunnen met behulp van de stelling van Pythagoras de waarde van $h$ bepalen: er geldt immers

$$R^2+3000^2=(R+h)^2.$$

We kunnen dus ook schrijven

$$h=\sqrt{R^2+3000^2}-R$$

of, met $R$ buiten de haakjes gehaald 

$$h=R\left(\sqrt{1+\left(\frac{3000}{R}\right)^2}-1\right).$$

Het quotiënt $\frac{3000}{R}$ is heel klein. Voor kleine $x$ is $\sqrt{1+x}$ vrijwel gelijk aan $1 + \frac12 x$, dit kun je nagaan door $1 + \frac12 x$ te kwadrateren en het resultaat met $1 + x$ te vergelijken. 
We krijgen zo een snelle benadering van $h$:

$$h\approx \frac12 R\left(\frac{3000}{R}\right)^2=\frac{3000^2}{2R}=\frac{9\pi}{40}.$$

Afgerond op drie significante cijfers vinden we $h \approx 0{,}707\mbox{ m}$. Dat klopt aardig met de metingen (of de metingen kloppen aardig met deze voorspelling). 

Alternatief 

Men was van plan de weg, eigenlijk een schelpenpad, op een dijk in Groningen te leggen. 

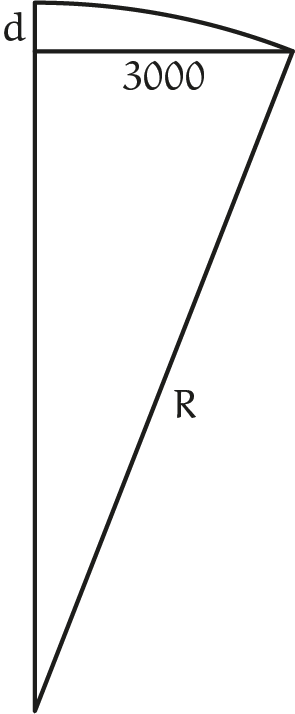
Figuur 2

Je zou de weg ook in kunnen graven, zoals in figuur 2; hoe diep komt hij in het midden dan te liggen? De diepte halverwege noemen we $d$. 

Dan geldt 

$$R^2=300^2+(R-d)^2,$$

als eerder leidt dit tot 

$$R-d=\sqrt{R^2-3000^2}$$

en dus 

$$d=R-\sqrt{R^2-3000^2}\approx\frac{3000^2}{2R}=\frac{9\pi}{40}.$$

De benaderingen van $h$ en $d$ zijn dus gelijk. 

Exacte antwoorden 

Als we de exacte formules gebruiken komen we uit op (in meters) 

$$h =0,7068583078154$$

en 

$$d=0,7068583863000.$$

Ik heb een programma gebruikt dat net zo nauwkeurig kan rekenen als je wilt; ik heb om dertig cijfers gevraagd en de resultaten bij dertien cijfers afgekapt.

De antwoorden vertellen ons twee dingen: de benadering wijkt inderdaad minder dan een millimeter af van de echte antwoorden (minder dan $0{,}15\mbox{ mm}$). 

Verder zien we dat $d$ groter is dan $h$, maar dat dat pas bij het achtste cijfer achter de komma te merken is. 

Om over na te denken

Opgave 1

Kun je zelf verklaren waarom $d$ groter is dan $h$?

Opgave 2

Men wilde de weg maken door schelpen te storten. Het pad zou $120\mbox{ cm}$ breed worden; hoeveel kubieke meter schelpen zou dat vergen?

Opgave 3

Als men zou gaan uitgraven, hoeveel kubieke meter grond moet er dan afgevoerd worden? Meer of minder dan er schelpen aangevoerd moeten worden?

Bekijk oplossing