Opgave 549 ^[oOO] 

Bas heeft een wiskundeboek waarvan de pagina’s genummerd zijn van $1$ tot en met $549$. Hij telt alle cijfers die voorkomen in de paginanummers bij elkaar op. Wat is dan de uitkomst?

Opgave 550 ^[oOO]

Omdat $1 = 1^2 - 0^2$ en $5 = 3^2 - 2^2$, zijn de getallen $1$ en $5$ te schrijven als het verschil tussen twee kwadraten. Hoeveel van de getallen $1$ tot en met $100$ hebben deze eigenschap?

Opgave 551 ^[ooO]

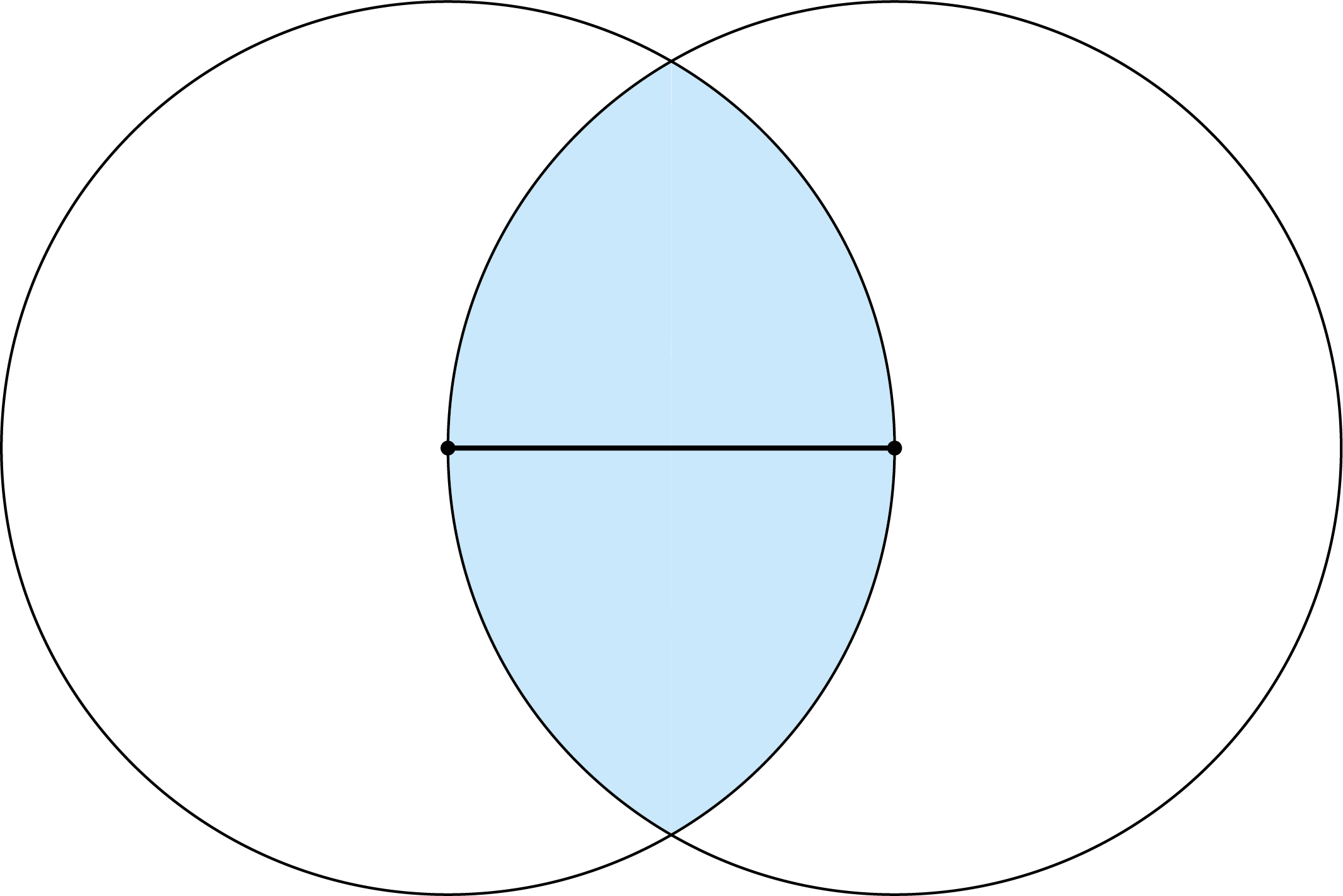
Twee punten hebben een onderlinge afstand van $6$. We tekenen twee cirkels met middelpunten het ene punt die gaan door het andere punt. Bepaal de oppervlakte van het overlappende gebied tussen de twee cirkels.

Opgave 552 ^[ooO]

We noemen een deler $d$ van een positief geheel getal $N$ echt als $d \neq 1$ en $d \neq N$. Zo zijn $2$ en $3$ echte delers van het getal $6$ en priemgetallen hebben nooit echte delers. Bepaal alle positieve gehele getallen $N$ met minstens twee echte delers en met de eigenschap dat als $d > e$ twee verschillende echte delers zijn van $N$, dan is $d - e$ ook een (niet noodzakelijk echte) deler van $N$.