
Tegels 3-4-6
Op het omslag van Pythagoras 59-1 van september 2019 staat een patroon, opgebouwd uit driehoeken, vierkanten en zeshoeken. Dit is één van de vele manieren om met deze drie vormen een vlakvulling te maken. In dit nummer onderzoeken we een aantal vlakvullingen die ook gebruik maken van regelmatige driehoeken, vierkanten en zeshoeken.
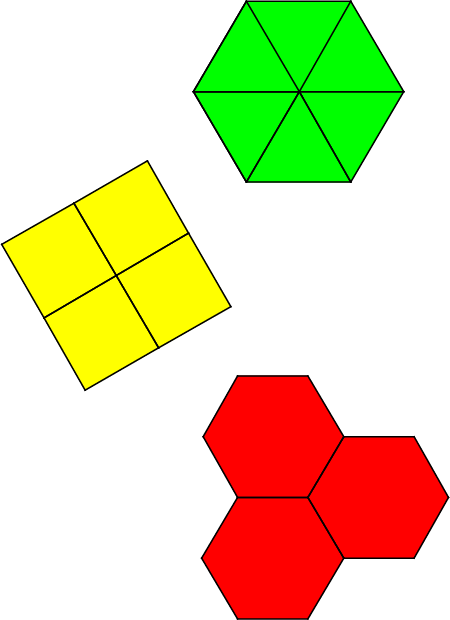
Om een grote muur te betegelen wil je gebruik maken van mooie symmetrische figuren in een herkenbaar patroon. De meest symmetrische figuur is de cirkel. Maar met cirkels zou je of gaten moeten laten vallen of overlappingen toestaan. De volgende figuren die in aanmerking komen zijn de regelmatige veelhoeken. Dat zijn veelhoeken met alle hoeken en alle zijden gelijk. In slechts drie gevallen zijn de hoeken van zo’n veelhoek delers van $360^{\rm o} $ en dus bruikbaar om een betegeling met één vorm zonder gaten of overlappingen te maken. Dit zijn de bekende regelmatige driehoek, vierkant en zeshoek in figuur 1.
Wij kunnen hun tegelpatronen digitaal coderen als $3-3-3-3-3-3$, $4-4-4-4$, en $6-6-6$. De getallen geven aan wat gebeurt in een punt waar $6$ driehoeken, $4$ vierkanten, of $3$ zeshoeken op elkaar aansluiten. En aangezien dat op elk punt op dezelfde manier gebeurt, kunnen zij dienen als digitale codenamen voor het hele tegelpatroon. Wat hierna volgt gaat alleen over deze drie vormen.
Als je dit een beetje saai vindt zou je het interessanter kunnen maken door een tegelpatroon te maken waar je twee van deze drie vormen gebruikt. Dit is de context voor de eerste drie vragen.
Opgave 1Ga na dat een vlakvulling mogelijk is waar in elk punt de code $4-4-3-3-3$ geldt. Dit is een volgordegevoelige code (dus niet alleen $2$ keer een vier en $3$ keer een drie) voor het hele patroon. Vind nog drie andere patronen met een volgordegevoelige code die gebruik maken van twee van de drie vormen. Wat zijn de mogelijkheden als je vasthoudt aan de eis dat in elk punt precies hetzelfde gebeurt en wat zijn dan hun volgordegevoelige digitale codes? Opgave 2Zijn er ook tegelpatronen waar op elk punt dezelfde vormen bij elkaar komen maar waar de volgorde niet hetzelfde is voor ieder punt? Hier kunnen we dus wel een volgordegevoelige digitale code geven voor elk punt apart maar niet één code voor het hele patroon. Opgave 3Als we alle sluitende patronen toelaten, zijn er oneindig veel mogelijkheden. Laat wat voorbeelden zien. |
Om het nog interessanter te maken kun je proberen een tegelpatroon te maken dat alle drie vormen gebruikt.
Opgave 4Als je alle drie de vormen wilt gebruiken voor een sluitend punt, wat zijn dan de mogelijke volgordegevoelige codes? Opgave 5Is er een tegelpatroon dat alle drie vormen gebruikt en waar dezelfde volgordegevoelig code geldt voor ieder punt? Opgave 6Zijn er ook tegelpatronen die alle drie de vormen gebruiken en waar op elk punt dezelfde vormen bij elkaar komen maar waar de volgorde niet altijd hetzelfde is? |
Net als in het geval waar je slechts twee vormen gebruikt is het met drie vormen mogelijk oneindig veel sluitende patronen te maken.
Opgave 7Laat wat voorbeelden zien. |
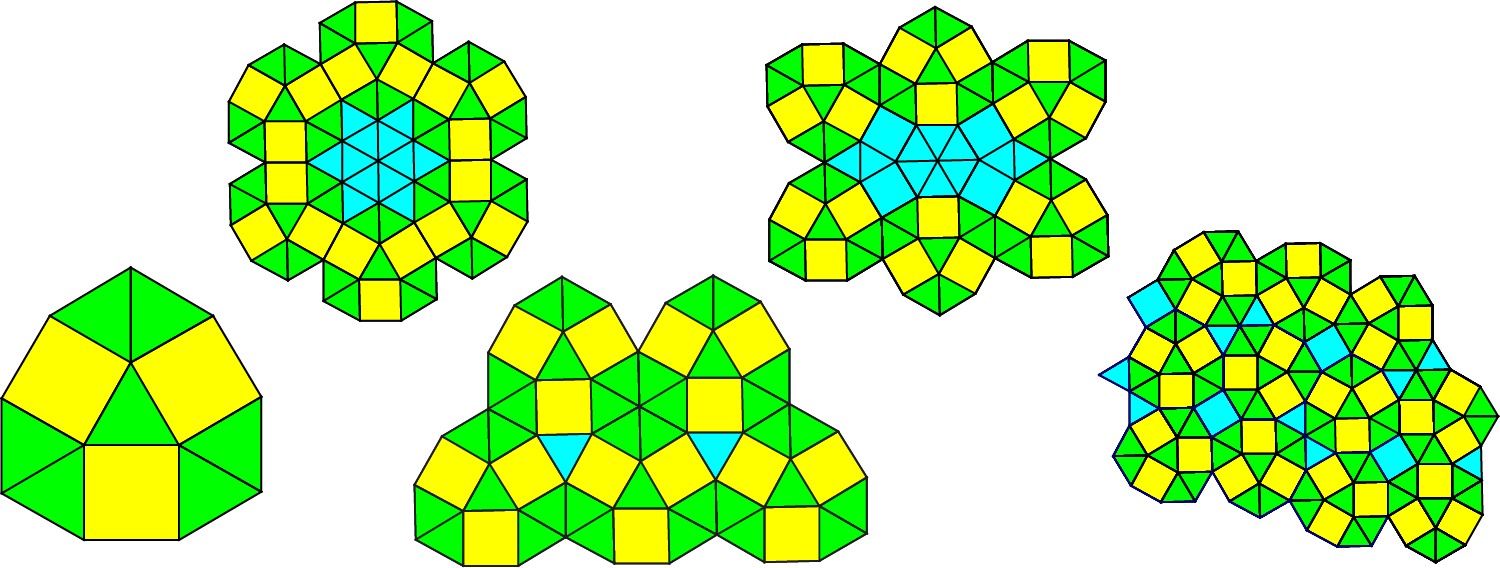
Soms is het mogelijk om een ingewikkeld tegelpatroon op te bouwen uit kleinere modules. Als voorbeeld neem ik de module links in figuur 2 met $7$ driehoeken en $3 $ vierkanten. Je ziet ook vier tegelpatronen die opgebouwd kunnen worden uit deze module. Soms komen er gaten tussen die weer opgevuld kunnen worden met de basis vormen. Deze opvullingen kleur ik blauw.
|
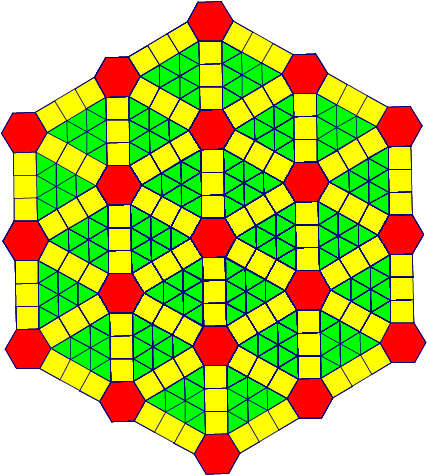
Het is ook mogelijk om patronen te ontwikkelen vanuit een centraal punt. In figuur 3 zie je een voorbeeld van een landschaps-patroon met rotondes, wegen en velden. Als je de lengte van de wegen $n$ noemt en het aantal lagen $m$ dan is in dit geval $n = 3$ en $m = 2$. Dit is dus een eindig patroon dat altijd nog verder uitgebreid kan worden. Ik noem het aantal nodige groene veldstukken $ v$, het aantal nodige gele wegstukken $w$, en het aantal nodige rode rotondestukken $r$. In dit geval geldt $r = 19$, $w = 126$ en $v = 216. $
Opgave 9Wat zijn de algemene formules voor $v, w$, en r in zo’n patroon, waar de wegen lengte n hebben en er m laagjes zijn? |
Bekijk oplossing

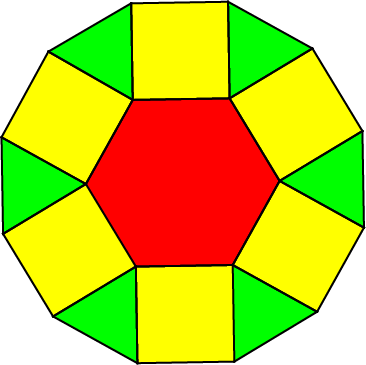 Opgave 8
Opgave 8